Otáčející se nabitá kulička kolem druhé stejně nabité kuličky
Úloha číslo: 954
Kulička o hmotnosti m a s nábojem q se může otáčet ve vertikální rovině na niti délky l. V ose otáčení je upevněna druhá kulička se stejným nábojem. Jakou minimální rychlost ve vodorovném směru je nutno udělit kuličce v dolní poloze, aby vykonala celou otáčku?
Pozn.: Jedná se v podstatě o kyvadlo.
Nápověda 1
Zamyslete se, kde je kritické místo, ve kterém by kulička nemusela dokončit celou otočku. Co v tomto místě musí platit, aby otočka byla dokončena.
Nápověda 2: Jak zjistit minimální rychlost?
Využijte zákon zachování mechanické energie. Zamyslete se nad volbou nulové hladiny potenciální energie.
Rozbor
O tom, zda kulička vykoná celou otočku, se rozhodne při průchodu nejvyšším bodem trajektorie. Proto si musíme uvědomit, jaké síly budou na kuličku v tomto bodě působit. Pomocí 2. Newtonova zákona určíme minimální rychlost v tomto bodě.
Minimální rychlost udělenou na počátku pohybu, tedy v nejnižším bodě kruhové trajektorie, určíme ze zákona zachování mechanické energie.
Řešení
O tom, zda kulička vykoná celou otočku, se rozhodne při průchodu nejvyšším bodem trajektorie. Proto si musíme uvědomit, jaké síly budou na kuličku v tomto bodě působit. Nakreslíme si obrázek.
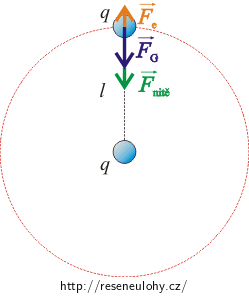
Podrobný komentář k silám je proveden v Řešení nápovědy 2, proto zde uvedeme jen výsledek úvah. V nejvyšším bodě trajektorie je síla nitě nulová a výslednice se musí rovnat dostředivé síle \(\vec{F}_\mathrm {do}\). Síly leží v jedné přímce, proto pro jejich velikosti platí
\[F_\mathrm {do}=F_\mathrm G-F_\mathrm e.\]Síly vyjádříme a získáme rovnici
\[ma_\mathrm d=mg-\frac{1}{4\pi\epsilon_0}\frac{q^2}{l^2}, \]kde m je hmotnost kuličky, g tíhové zrychlení, l délka nitě, ε0 permitivita vakua, která je přibližně stejná jako permitivita vzduchu, a q náboj, který je pro obě kuličky stejný. Dostředivé zrychlení ad se dá vyjádřit pomocí rychlosti v nejvyšším bodě v a délky nitě l jako \(a_\mathrm d=\frac{{v}^2}{l}\). Po dosazení dostáváme
\[m\frac{{v}^2}{l}=mg-\frac{1}{4\pi\epsilon_0}\frac{q^2}{l^2}.\]Z tohoto vztahu vyjádříme v2, což je kvadrát minimální nutné rychlosti v nejvyšším bodě trajektorie:
\[ v^2=\frac{(mg-\frac{1}{4\pi\epsilon_0}\frac{q^2}{l^2})l}{m}. \]My však nemáme určit v, nýbrž minimální rychlost udělenou na počátku pohybu, tedy v nejnižším bodě kruhové trajektorie. Tuto rychlost označíme vm a uvážíme, jak souvisí s v. Vyjdeme ze zákona zachování mechanické energie. Součet kinetické a potenciální tíhové energie kuličky je stálý. Při volbě nulové hladiny potenciální energie v nejnižším bodě trajektorie platí, že kinetická energie v nejnižším bodě trajektorie Ek1 je rovna součtu kinetické energie v nejvyšším bodě trajektorie Ek2 a potenciální energie Ep:
\[ E_\mathrm {k1}=E_\mathrm {k2}+E_\mathrm p. \]Energie vyjádříme a dostáváme rovnici
\[ \frac{1}{2}m v_\mathrm {m}^2 = \frac{1}{2}m v^2 + 2mgl. \]Z tohoto vztahu vyjádříme vm tak, že rovnici vydělíme m a vynásobíme dvěma:
\[ v_\mathrm m=\sqrt{v^2 +4gl}. \]Nyní už jen dosadíme za v:
\[ v_\mathrm m=\sqrt{\frac{(mg-\frac{1}{4\pi\epsilon_0}\frac{q^2}{l^2})l}{m} +4gl}= \sqrt{5gl - \frac{q^2}{4\pi\epsilon_0 m l}} .\]Odpověď
Minimální rychlost, kterou musíme udělit kuličce, je dána vztahem
\[v_\mathrm m=\sqrt{5gl - \frac{q^2}{4\pi\epsilon_0 m l}}.\]Odkaz na úlohu řešenou podobnou strategií


