Ekvipotenciální plocha
Úloha číslo: 2025
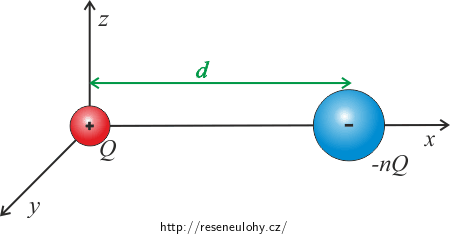
Bodový náboj o velikosti Q leží v počátku souřadného systému, bodový náboj o velikosti −nQ v místě o souřadnicích (d, 0, 0), n > 0, d > 0. Jaký tvar má plocha, na které je potenciál roven potenciálu v nekonečnu?
Nápověda – elektrický potenciál
Potenciál v nekonečnu obvykle volíme roven nule. Při této volbě má potenciál bodového náboje Q ve vzdálenosti r od tohoto náboje velikost
\[\varphi = k\frac{Q}{r}.\]Rozbor
Obvykle pokládáme potenciál v nekonečnu roven 0, to učiníme i v této úloze. Budeme tedy hledat místa, kde je celkový potenciál nulový. Celkový potenciál v daném místě získáme jako součet potenciálů od obou nábojů.
Uvažujme libovolný bod B v prostoru o souřadnicích \(\textrm{B} = [x;y;z].\)
Je-li \(\varphi_1\) potenciál v bodě B od náboje Q a \(\varphi_2\) potenciál v bodě B od náboje −nQ, pak musí platit
\[\varphi_1 + \varphi_2 = 0.\tag{1}\]Zbývá vyjádřit potenciál \(\varphi_1\) a \(\varphi_2\) v bodě B od obou nábojů a řešit uvedenou rovnici.
Řešení
Abychom vyjádřili \(\varphi_1\) a \(\varphi_2\), nakreslíme si celou situaci do kartézských souřadnic. Bod B je obecný bod v prostoru popsaný souřadnicemi \(\textrm{B} = [x; y; z].\)
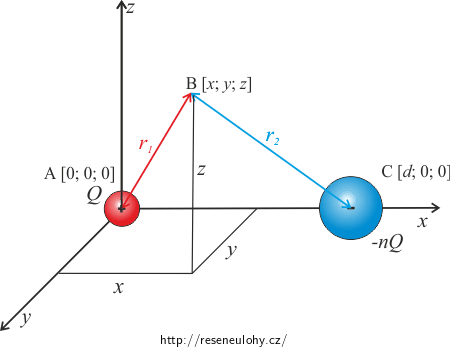
Začněme s vyjádřením potenciálu \(\varphi_1\), který v bodě B vytváří náboj Q:
\[\varphi_1 = k \frac {Q}{r_1},\tag{2}\]kde \(r_1\) je vzdálenost bodu B od bodového náboje Q. Protože známe souřadnice obou bodů, vzdálenost \(r_1\) spočteme jako
\[r_1 = \sqrt{(0-x)^2 + (0-y)^2 + (0-z)^2,}\] \[r_1 = \sqrt{x^2 + y^2 + z^2.}\tag{3}\] \[\varphi_1 = k \frac {Q}{\sqrt{x^2 + y^2 + z^2}}.\tag{4}\]Analogicky vyjádříme potenciál \(\varphi_2\) v bodě B od náboje −nQ
\[\varphi_2 = k \frac {-nQ}{r_2},\tag{5}\]kde \(r_2\) je vzdálenost bodu B od bodového náboje −nQ:
\[r_2 = \sqrt{(d-x)^2+(0-y)^2+(0-z)^2},\] \[r_2 = \sqrt{(d-x)^2 + y^2 + z^2}.\tag{6}\] \[\varphi_2 = k \frac {-nQ}{\sqrt{(d-x)^2 + y^2 + z^2}}.\tag{7}\]Vzhledem k tomu, že pro potenciál bodového náboje používáme vztah, ve kterém je v nekonečnu nulový potenciál, hledáme body, pro které platí
\[\varphi_1 + \varphi_2 = 0.\]Dosadíme vyjádření potenciálů (4) a (7):
\[k \frac {Q}{\sqrt{x^2 + y^2 + z^2}} + k \frac {-nQ}{\sqrt{(d-x)^2 + y^2 + z^2}} = 0\]a rovnici upravíme:
\[k \frac {Q}{\sqrt{x^2 + y^2 + z^2}} = k \frac {nQ}{\sqrt{(d-x)^2 + y^2 + z^2}},\] \[ \frac {1}{\sqrt{x^2 + y^2 + z^2}} = \frac {n}{\sqrt{(d-x)^2 + y^2 + z^2}},\] \[ \sqrt{(d-x)^2 + y^2 + z^2} = {n}\sqrt{(x^2 + y^2 + z^2)}.\qquad\]Protože jsou obě strany rovnosti kladné, umocníme ji na druhou a upravíme:
\[ (d-x)^2 + y^2 + z^2 = {n^2}(x^2 + y^2 + z^2),\qquad\] \[ d^2 - 2xd + x^2 + y^2 + z^2 = n^2x^2 + n^2y^2 + n^2z^2,\qquad\] \[\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad d^2 = (n^2-1)x^2 + 2xd + (n^2-1)y^2 + (n^2-1)z^2.\]V rovnici se vyskytují členy typu \(x^2, y^2\) atp., což nás vede k myšlence, že by se mohlo jednat o tzv. kvadratickou plochu (mezi ně patří např. kulová plocha, elipsoid, hyperbolická plocha...).
Zdá se, že by bylo výhodné rovnici vydělit výrazem \(n^2 -1\). Ten je ale pro \(n=1\) nulový, proto teď budeme řešit za podmínky \(n\neq 1\) a případ \(n=1\) vyřešíme později:
\[ \frac{d^2}{n^2-1} = x^2 + 2\frac {d}{n^2-1}x + y^2 + z^2.\]Na pravé straně členy s x doplníme na úplný čtverec:
\[ \qquad \qquad \qquad \frac{d^2}{n^2-1} = \left(x + \frac {d}{n^2-1}\right)^2 - \left(\frac {d}{n^2-1}\right)^2 + y^2 + z^2\]a upravíme:
\[ \frac{d^2}{n^2-1} + \frac {d^2}{(n^2-1)^2} = \left(x + \frac {d}{n^2-1}\right)^2 + y^2 + z^2,\] \[ \frac {d^2n^2}{(n^2-1)^2} = \left(x + \frac {d}{n^2-1}\right)^2 + y^2 + z^2.\]Poslední výraz je středová rovnice kulové plochy se středem \(S = \left[-\frac{d}{n^2 -1},0{,}0\right]\) a poloměrem \(R = \frac {dn}{n^2 -1}\), což je hledaná plocha.
Nyní se vrátíme k případu \(n=1\):
\[ d^2 = (n^2-1)x^2 + 2xd + (n^2-1)y^2 + (n^2-1)z^2,\] \[ d^2 = (1^2-1)x^2 + 2xd + (1^2-1)y^2 + (1^2-1)z^2,\] \[ d^2 = 2xd,\] \[ x = \frac {d}{2}.\]Pro \(n=1\) je místem s nulovým potenciálem rovina popsaná rovnicí \( x=\frac {d}{2},\) což je rovina kolmá na osu x, která ji protíná v bodě \([\frac{d}{2}; 0; 0].\)
Pro \(n=1\) mají oba náboje stejnou velikost a opačná znaménka, potenciál se „vynuluje“ v místech, která mají stejnou vzdálenost od obou nábojů, tedy leží v rovině jejich symetrie.
Odpověď
Pro \(n>0 \wedge n\not=1\) je plocha, na které je potenciál roven potenciálu v nekonečnu, kulová plocha se středem \(S = \left[-\frac{d}{n^2 -1}; 0; 0\right]\) a poloměrem \(R = \frac {dn}{n^2 -1}\). Pro \(n=1\) je to rovina popsaná rovnicí \( x=\frac {d}{2},\) což je rovina kolmá na osu x, která ji protíná v bodě \([\frac{d}{2}; 0; 0].\)
Komentář – zjednodušený výpočet vzdálenosti
V řešení je vzdálenost bodu B od nábojů spočítána pomocí vztahů z analytické geometrie. Lze to ale vyjádřit i bez nich.
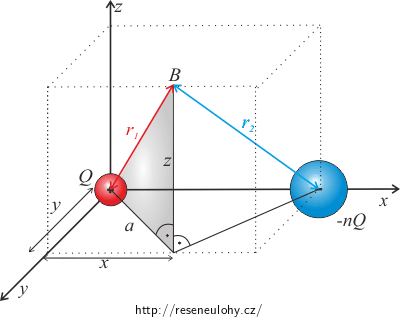
Bod B je obecný bod v prostoru popsaný souřadnicemi \(B = [x;y;z].\)
Na obrázku lze vidět, že
\[r_1 = \sqrt{a^2 + z^2}\tag{8}\]a
\[a^2 = x^2 + y^2.\tag{9}\] \[r_1 = {\sqrt{x^2 + y^2 + z^2}}.\tag{10}\]Analogicky vyjádříme vzdálenost \(r_2\) od náboje −nQ:
\[r_2 = \sqrt{b^2 + z^2}\tag{11}\]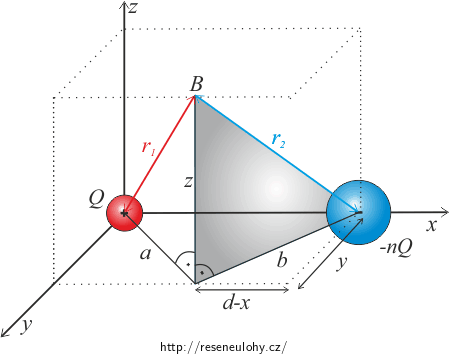
a
\[b^2 = (d-x)^2 + y^2.\tag{12}\]Spojením (11) a (12) dostaneme
\[r_2 = {\sqrt{(d-x)^2 + y^2 + z^2}}.\tag{13}\]Interaktivní program
Situaci, kterou popisuje úloha, znázorňuje i interaktivní demonstrační program. Stáhněte si ho a k jeho spuštění použijte Wolfram CDF Player.
Program ukazuje potenciál pole, které vytvářejí dva bodové náboje v uspořádání stejném jako v této úloze. Pole je naznačeno pomocí ekvipotenciálních ploch a hodnota potenciálu zvýrazněna barvou — kladné hodnoty odstíny červené a záporné hodnoty odstíny modré. Ekvipotenciála odpovídající nulovému potenciálu (potenciálu v nekonečnu) má kolem sebe bílé plochy.
- Zkuste v programu měnit podíl velikostí obou nábojů n a sledujte tvar ekvipotenciály pro nulový potenciál. Jedná se opravdu o kouli? (Pozn.: Koule bude na řezu rovinou znázorněna kružnicí.)
- Nastavte n = 1, tj. dva stejně velké náboje opačného znaménka. Odpovídá poloha nulové ekvipotenciály vašemu očekávání? Odpovídá spočítanému výsledku?
- Zvětšujte n a sledujte, zda chování velikosti poloměru a polohy středu odpovídá výsledku.
- Zkontrolujte získané výsledky i numericky pro hodnoty např. n = 2 a n = 1/2.

