Vodič a náboj
Úloha číslo: 763
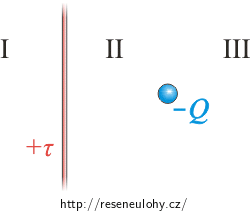
Ve vzdálenosti a od přímého nekonečně dlouhého vodiče s lineární hustotou náboje +τ se nachází bodový náboj −Q.
V jaké oblasti (viz obr.) leží body, v nichž je intenzita celkového elektrického pole rovna nule? Proveďte diskuzi počtu řešení.
Nápověda 1: Intenzita pole vodiče a náboje
Pro intenzitu elektrického pole bodového náboje platí:
\[E_\mathrm{Q}\,=\,\frac{1}{4 \pi \varepsilon_0}\,\frac{Q}{r^2}\,,\]kde r je vzdálenost od náboje.
Pro pole vodiče:
\[E\,=\,\frac{1}{2 \pi \varepsilon_0}\,\frac{\tau}{r}\,,\]kde r je vzdálenost od vodiče.
Podrobně je intenzita elektrického pole v okolí vodiče vypočítána v úloze Pole nabité přímky.
Nápověda 2
Uvědomte si, co musí platit pro směr a velikost vektorů intenzit elektrického pole vodiče a náboje, aby celková intenzita byla rovna nule.
Kde může tato situace nastat?
Nápověda 3
Vzdálenost bodů s nulovou intenzitou od vodiče, resp. od náboje získáme řešením kvadratické rovnice. Řešením jsou ale pouze reálné kladné kořeny, protože počítáme vzdálenost, která nemůže být záporná.
Rozbor
Aby v nějakém bodě byla intenzita rovna nule, musí mít vektory intenzit elektrických polí vyvolaných přímým vodičem a bodovým nábojem stejnou velikost a opačný směr.
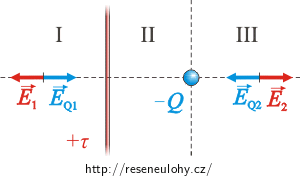
Vektor intenzity elektrického pole záporného bodového náboje míří směrem k náboji. Intenzita elektrického pole vodiče míří směrem od vodiče. Z toho plyne, že oba vektory mohou mít opačný směr pouze v oblastech I a III. Zároveň se tato místa musí nacházet na kolmici k vodiči, která prochází bodovým nábojem.
Z rovnosti velikosti intenzity elektrického pole vodiče a náboje získáme v obou oblastech kvadratickou rovnici pro vzdálenost bodu s nulovou intenzitou. Protože se jedná o vzdálenost, jsou řešením úlohy pouze kladné reálné kořeny rovnic.
Řešení
Aby v nějakém bodě byla intenzita rovna nule, musí mát vektory intenzity elektrických polí vyvolaných přímým vodičem a bodovým nábojem stejnou velikost a opačný směr. Podmínka na opačný směr však může být zřejmě splněna pouze na kolmici k drátu, jež prochází bodovým nábojem, a to ještě pouze v oblastech I a III.

Poznámka: Obrázek zachycuje pouze směry vektorů elektrických intenzit v jednotlivých oblastech, nikoli jejich velikosti. Modře je zakreslena intenzita elektrického pole náboje a červeně intenzita elektrického pole vodiče.
Pomocí podmínky na stejnou velikost obou intenzit vyhledáme nejprve bod či body s celkovou nulovou intenzitou elektrického pole v oblasti III a poté v oblasti I.
Ještě zde uvedeme vztahy pro výpočet velikosti intenzity elektrického pole bodového náboje a vodiče, které budeme později potřebovat.
Pro pole bodového náboje o velikosti Q platí:
\[E_\mathrm{Q}\,=\,\frac{1}{4 \pi \varepsilon_0}\,\frac{Q}{r^2}\,,\tag{1}\]kde r je vzdálenost od náboje.
Pro pole vodiče nabitého s lineární hustotou náboje τ:
\[E\,=\,\frac{1}{2 \pi \varepsilon_0}\,\frac{\tau}{r}\,,\tag{2}\]kde r je vzdálenost od vodiče.
Řešení v oblasti III
Z požadavku na stejnou velikost intenzit od bodového náboje a přímého vodiče získáme s použitím vztahů (1) a (2) pro výpočet intenzity těchto prvků (viz předchozí oddíl) rovnost \[E_2\,=\,E_\mathrm{Q2},\] \[\frac{1}{2 \pi \varepsilon_0}\,\frac{\tau}{a+y}, \,=\,\frac{1}{4 \pi \varepsilon_0}\,\frac{Q}{y^2}\,,\]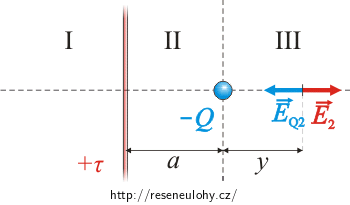
kde y udává vzdálenost hledaného bodu od bodového náboje.
Jednoduchými úpravami získáme kvadratickou rovnici pro neznámou y:
\[\frac{\tau}{a+y} \,=\,\frac{Q}{2y^2} \hspace{40px}|\cdot 2y^2\left(a+y\right),\] \[2 \tau y^2 \,=\, Q\left(a+y\right),\] \[2 \tau y^2 \,-\,Qy \,-\,Qa \,=\, 0.\]Kvadratickou rovnici vyřešíme:
\[ y_{1{,}2}\,=\,\frac{Q \pm \sqrt{Q^2 + 8 \tau Q a}}{4 \tau}.\]Nyní musíme získaný výsledek správně interpretovat. Vidíme, že diskriminant kvadratické rovnice je kladný pro všechny přípustné hodnoty parametrů a, Q a τ. Kvadratická rovnice tedy má dva reálné kořeny. Protože platí
\[Q \lt \sqrt{Q^2 + 8 \tau Q a},\]bude jeden z kořenů vždy kladný a druhý záporný. Záporný kořen je pro nás vzhledem k tomu, že počítáme vzdálenost, nepřijatelný. Vyhovovat nám tedy bude pouze kladné řešení, a to
\[ y\,=\,\frac{Q + \sqrt{Q^2 + 8 \tau Q a}}{4 \tau}\,.\]V oblasti III tedy bude vždy existovat právě jeden bod s nulovou výslednou intenzitou elektrického pole. Pro jeho vzdálenost od bodového náboje platí vztah
\[ y\,=\,\frac{Q + \sqrt{Q^2 + 8 \tau Q a}}{4 \tau}\,.\]Řešení v oblasti I
Nyní přistoupíme k hledání bodů s nulovou intenzitou v oblasti I. Využijeme vztahů (1) a (2) z předchozího oddílu.
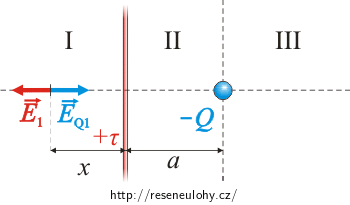
Z podmínky na stejnou velikost intenzit od bodového náboje a dlouhého přímého vodiče získáme rovnost
\[E_1\,=\,E_\mathrm{Q1}\,.\] \[\frac{1}{2 \pi \varepsilon_0}\,\frac{\tau}{x} \,=\,\frac{1}{4 \pi \varepsilon_0}\,\frac{Q}{\left(a+x\right)^2}\,,\]kde x je vzdálenost hledaného bodu od vodiče.
Postupnými úpravami se opět dostaneme ke kvadratické rovnici pro neznámou x:
\[\frac{\tau}{x} \,=\,\frac{Q}{2\left(a+x\right)^2}\,\hspace{40px}|\cdot 2x\left(a+x\right)^2,\] \[2\tau \left(a+x\right)^2 \,=\,Qx,\] \[2\tau a^2\,+\,4\tau ax\,+\,2 \tau x^2 \,=\,Qx,\] \[2 \tau x^2 \,+ \left(4\tau a - Q \right) x\,+\,2\tau a^2 \,=\,0.\]Nejprve si vyjádříme diskriminant D této rovnice
\[ D=\left(4\tau a - Q \right)^2-4{\cdot}2\tau \cdot 2\tau a^2 = Q^2 - 8\tau a Q.\]Protože hledáme kladná reálná řešení, musí být diskriminant nezáporný. Dostáváme tedy podmínku:
\[Q\ge 8a\tau.\]Napíšeme vztah pro kořeny rovnice:
\[ x_{1{,}2}\,=\,\frac{Q \,-\, 4\tau a \,\pm \sqrt{\left(Q \,-\, 4\tau a\right)^2 \,-\, 16 \tau^2 a^2}}{4 \tau}.\]Člen Q − 4aτ je jistě kladný (viz podmínka kladnosti diskriminantu) a z tvaru výrazu pod odmocninou je vidět, že odmocnina je menší než hodnota, která stojí před ní. Kořeny rovnice jsou tedy kladné.
Souhrnně:
Jestliže Q < 8aτ, potom rovnice nemá řešení a místo s nulovou intenzitou v oblasti I neexistuje.
Jestliže Q = 8aτ, rovnice má jeden dvojný kladný kořen. Nulová intenzita je tedy ve vzdálenosti x = a od vodiče.
Jestliže Q > 8aτ, potom rovnice má dva kladné kořeny. Místa s nulovou intenzitou jsou vzdálena od vodiče:
\[ x_{1{,}2}\,=\,\frac{Q \,-\, 4\tau a \,\pm \sqrt{\left(Q \,-\, 4\tau a\right)^2 \,-\, 16 \tau^2 a^2}}{4 \tau}.\]
Odpověď
V oblasti III existuje vždy právě jeden bod s nulovou výslednou intenzitou elektrického pole. Pro jeho vzdálenost od bodového náboje platí vztah
\[ y_1\,=\,\frac{Q + \sqrt{Q^2 + 8 \tau Q a}}{4 \tau}\,.\]V oblasti I mohou být řešení dvě, jedno nebo žádné:
Jestliže Q < 8aτ, potom rovnice nemá řešení a místo s nulovou intenzitou v oblasti I neexistuje.
Jestliže Q = 8aτ, rovnice má jeden dvojný kladný kořen. Nulová intenzita je tedy ve vzdálenosti x = a od vodiče.
Jestliže Q > 8aτ, potom rovnice má dva kladné kořeny. Místa s nulovou intenzitou jsou vzdálena od vodiče
\[ x_{1{,}2}\,=\,\frac{Q \,-\, 4\tau a \,\pm \sqrt{\left(Q \,-\, 4\tau a\right)^2 \,-\, 16 \tau^2 a^2}}{4 \tau}.\]


