Amplituda proudu při proměnné frekvencí zdroje
Úloha číslo: 171
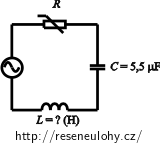
Zápis
Ze zadání známe:
Kapacitu kondenzátoru: C = 5,5 μF = 5,5·10-6 F Odpor reostatu: Ra = 100 Ω Odpor reostatu: Rb = 2000 Ω Proud v obvodu je poloviční než proud maximální: Im = 1/2 Imax Frekvenci napětí zdroje pro úkol za a): f1 = 1,3 kHz f2 = 1,5 kHz Chceme určit:
a) Indukčnost cívky: L = ? (H) b) Frekvenci napětí zdroje při nastaveném odporu rezistoru na 2000 Ω tak, aby proud v obvodu byl poloviční než proud maximální: f3 = ? (Hz) f4 = ? (Hz) Nápověda 1
Za jakých podmínek teče obvodem maximální střídavý proud? Lze této podmínky dosáhnout změnou frekvence?
Nápověda 2
Z Ohmova zákona pro střídavý proud vyplývá, že maximální střídavý proud poteče obvodem, pokud celková impedance bude minimální. Jak je třeba nastavit frekvenci zdroje, abychom dosáhli minimální impedance?
Rozbor
a) Chceme vyjádřit indukčnost cívky. Známe vztah pro proudy v obvodu a víme, že platí Ohmův zákon pro střídavý proud. V Ohmově zákoně vystupuje indukčnost cívky ve výpočtu impedance, takže se budeme snažit pomocí tohoto zákona vyjádřit impedanci v obvodu.
Maximální proud teče obvodem při takové frekvenci, kdy se kapacitance kondenzátoru rovná induktanci cívky. V takovém případě se totiž celková impedance rovná rezistanci (nezávislé na frekvenci) a je minimální. Pomocí Ohmova zákona pro střídavý proud vyjádříme maximální hodnotu proudu z amplitudy napětí a rezistance. Toto vyjádření maximálního proudu dosadíme do vztahu mezi maximálním proudem a amplitudou proudu při zadaných frekvencích. Tím zjistíme celkovou impedanci obvodu.
Určili jsme impedanci obvodu a chceme vypočítat indukčnost cívky. Můžeme použít vzorec pro výpočet impedance. Rovnici nejdříve vyřešíme obecně, poté dosadíme frekvence zdroje, které známe ze zadání, a indukčnost cívky vyjádříme v závislosti na obou frekvencích.
b) Frekvence, pro které platí, že amplituda proudu v obvodu je rovna polovině maximální hodnoty proudu při změněném odporu rezistoru, vypočteme pomocí impedance. Velikost impedance jsme odvodili ze vztahu mezi maximálním proudem a amplitudou proudu. Dosadíme do ní nyní již známe hodnoty kapacity, odporu a indukčnosti a z rovnice vyjádříme neznámou frekvenci.
Řešení - Impedance obvodu, pro který platí, že Im=Imax/2
Maximální proud poteče obvodem při rezonanci, při které je impedance rovna rezistanci. Podle Ohmova zákona platí:
\[I_{\mathrm{max}}=\frac{U_\mathrm{m}}{Z}=\frac{U_\mathrm{m}}{R}.\]Ze zadání známe vztah mezi amplitudou proudu Im pro dvě zadané frekvence a maximálním proudem Imax:
\[I_\mathrm{m}=\frac{I_{\mathrm{max}}}{2}.\]Dosadíme vztah pro maximální proud:
\[I_\mathrm{m}=\frac{\frac{U_\mathrm{m}}{R}}{2}=\frac{U_\mathrm{m}}{2R}.\]Za amplitudu proudu dosadíme také z Ohmova zákona. To znamená, že impedance obvodu při zadaných frekvencích je:
\[Z=2R.\]a) Řešení - Indukčnost cívky
Indukčnost cívky vyjádříme z obecného vztahu pro celkovou impedanci:
\[Z=\sqrt{\left(R_a\right)^2+\left(X_L-X_C\right)^2}.\]Dosadíme za impedanci Z = 2Ra:
\[2R_a=\sqrt{\left(R_a\right)^2+\left(\omega L-\frac{1}{\omega C}\right)^2}\] \[4\left(R_a\right)^2=\left(R_a\right)^2+\left(\omega L-\frac{1}{\omega C}\right)^2\] \[3\left(R_a\right)^2=\left(\omega L-\frac{1}{\omega C}\right)^2\] \[ \sqrt{3}R_a=\pm\left(\omega L-\frac{1}{\omega C}\right).\]Víme, že tento vztah má platit pro dvě frekvence f1 a f2, každá z nich odpovídá jednomu znaménku v posledním vztahu. Pro přehlednost si výsledek vyjádříme nejprve v odpovídajících úhlových frekvencích ω1 a ω2:
\[ \sqrt{3}R_a=+\left({\omega}_1 L-\frac{1}{{\omega}_1 C}\right),\] \[ \sqrt{3}R_a=-\left({\omega}_2 L-\frac{1}{{\omega}_2 C}\right).\]Řešíme soustavu rovnic. Rovnice od sebe odečteme:
\[ {\omega}_1 L-\frac{1}{{\omega}_1 C}=-\left({\omega}_2 L-\frac{1}{{\omega}_2 C}\right).\]Vyjádříme indukčnost:
\[L\left({\omega}_1+{\omega}_2\right)=\frac{1}{C}\left(\frac{1}{{\omega}_1}+\frac{1}{{\omega}_2}\right)= \frac{1}{C}\left(\frac{{\omega}_1+{\omega}_2}{{\omega}_1 {\omega}_2}\right)=\frac{1}{{\omega}_1 {\omega}_2 C}.\]Dosadíme za úhlové frekvence:
\[L=\frac{1}{\left(2 \pi f_1\right) \left(2 \pi f_2\right) C}=\frac{1}{\left(2 \pi\right)^2 f_1 f_2 C}.\]b) Řešení - frekvence zdroje napětí
Opět využijeme vztah pro celkovou impedanci obvodu:
\[Z=\sqrt{\left(R_b\right)^2+\left(X_L-X_C\right)^2}.\]Z předchozího oddílu Řešení - Indukčnost cívky víme, že požadovaný proud poteče obvodem, jestliže pro celkovou impedanci platí Z = 2Rb. Teď je ale naší neznámou frekvence. Naprosto stejnými úpravami jako v předchozím oddíle dostaneme:
\[3\left(R_\mathrm{b}\right)^2=\left(\omega L-\frac{1}{\omega C}\right)^2\] \[\sqrt{3}\left(R_\mathrm{b}\right)=\pm \left(\omega L-\frac{1}{\omega C}\right).\]Pro obě varianty si zvlášť vyjádříme frekvenci:
1) Kladné znaménko
\[\sqrt{3}R_\mathrm{b}= \left({\omega}_3 L-\frac{1}{{\omega}_3 C}\right)\ / \cdot {\omega}_3\] \[\sqrt{3}R_\mathrm{b}\, {\omega}_3= {{\omega}_3}^2 L-\frac{1}{ C} \] \[0= L {{\omega}_3}^2 -\sqrt{3}R_b\, {\omega}_3 - \frac{1}{ C} \]Vyřešíme kvadratickou rovnici:
\[{\omega}_3=\frac{\sqrt{3}R_\mathrm{b} \pm \sqrt{\left(\sqrt{3}R_\mathrm{b}\right)^2 + \frac{4L}{C}}}{2 L}.\]Fyzikálně smysluplné (tj. kladné) je pouze řešení:
\[{\omega}_3=\frac{\sqrt{3}R_\mathrm{b} + \sqrt{\left(\sqrt{3}R_\mathrm{b}\right)^2 + \frac{4L}{C}}}{2 L}.\]Vyjádříme frekvenci napětí zdroje:
\[f_3=\frac{{\omega}_3}{2\pi}=\frac{\sqrt{3}R_\mathrm{b} + \sqrt{\left(\sqrt{3}R_\mathrm{b}\right)^2 + \frac{4L}{C}}}{4 \pi L}.\]
2) Záporné znaménko:
\[\sqrt{3}R_\mathrm{b}= -\left({\omega}_4 L-\frac{1}{{\omega}_4 C}\right)\ / \cdot {\omega}_4\] \[\sqrt{3}R_\mathrm{b}\, {\omega}_4= -{{\omega}_4}^2 L + \frac{1}{ C} \] \[0= L {{\omega}_4}^2 +\sqrt{3}R_\mathrm{b}\, {\omega}_4 - \frac{1}{ C} \]Vyřešíme kvadratickou rovnici:
\[{\omega}_4=\frac{-\sqrt{3}R_\mathrm{b} \pm \sqrt{\left(\sqrt{3}R_\mathrm{b}\right)^2 + \frac{4L}{C}}}{2 L}.\]Fyzikálně smysluplné (tj. kladné) je pouze řešení:
\[{\omega}_4=\frac{-\sqrt{3}R_\mathrm{b} + \sqrt{\left(\sqrt{3}R_\mathrm{b}\right)^2 + \frac{4L}{C}}}{4 \pi L}.\]Vyjádříme frekvenci napětí zdroje:
\[f_4=\frac{{\omega}_4}{2\pi}=\frac{-\sqrt{3}R_\mathrm{b} + \sqrt{\left(\sqrt{3}R_\mathrm{b}\right)^2 + \frac{4L}{C}}}{4 \pi L}.\]Číselné dosazení
Indukčnost cívky:
\[L=\frac{1}{\left(2 \pi\right)^2 f_1 f_2 C}=\frac{1}{\left(2 \pi\right)^2{\cdot} 1300 \cdot 1500 {\cdot} 5{,}5 {\cdot} 10^{-6}}\,\mathrm{H} \,\dot{=}\, 2{,}4\,\mathrm{mH}\]
Frekvence napětí zdroje:
\[f_3=\frac{\sqrt{3}R_\mathrm{b} + \sqrt{\left(\sqrt{3}R_\mathrm{b}\right)^2 + \frac{4L}{C}}}{4 \pi L}=\frac{\sqrt{3} \cdot 2000 + \sqrt{\left(\sqrt{3} \cdot 2000\right)^2 + \frac{4{\cdot} 2{,}4 {\cdot} 10^{-3}}{5{,}5 {\cdot} 10^{-6}}}}{4 \pi \cdot 2{,}4{\cdot} 10^{-3}}\,\mathrm{Hz}\,\dot{=}\,230 \,\mathrm{ kHz}\]
\[f_4=\frac{-\sqrt{3}R_\mathrm{b} + \sqrt{\left(\sqrt{3}R_\mathrm{b}\right)^2 + \frac{4L}{C}}}{4 \pi L}=\frac{-\sqrt{3} \cdot 2000 + \sqrt{\left(\sqrt{3} \cdot 2000\right)^2 + \frac{4{\cdot} 2{,}4 {\cdot} 10^{-3}}{5{,}5 {\cdot} 10^{-6}}}}{4 \pi \cdot 2{,}4 {\cdot} 10^{-3}}\,\mathrm{Hz}\,\dot{=}\,8{,}4 \,\mathrm{ Hz}\]Odpověď
a) Indukčnost cívky v obvodu má hodnotu asi 2,4 mH.
b) Hodnoty frekvencí připadající k odporu 2000 Ω jsou přibližně 230 kHz a 8,4 Hz.


