Sbírka řešených úloh

Paralelní zapojení kondenzátorů

Úloha číslo: 158

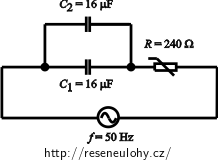
Sériový obvod střídavého proudu o frekvenci 50 Hz se skládá z reostatu s nastaveným odporem 240 Ω a dvou kondenzátorů o kapacitách C₁ = C₂ = 16 μF spojených paralelně. Kolikrát se změní proud v obvodu, jestliže jeden kondenzátor odpojíme? Jak musíme změnit odpor reostatu, aby obvodem procházel původní proud?

• Zápis

  Ze zadání známe:

  Frekvenci na zdroji:	f = 50 Hz
  Odpor reostatu:	R = 240 Ω
  Kapacity kondenzátorů:	C1 = C2  = 16 μF = 16·10-6 F

  Chceme určit:

  Změnu proudu při odpojení jednoho z kondenzátorů:	Im2/Im1 = ?
  Novou hodnotu odporu reostatu, aby po odpojení kondenzátoru tekl obvodem stejný proud:	Rx = ? (Ω)

• Nápověda 1

  Zapojíme-li kondenzátory paralelně, jejich kapacity se sčítají: \[C=C_1+C_2.\]

• Nápověda 2

  Pro výpočet použijeme Ohmův zákon pro střídavý proud \(I_\mathrm{m}=\frac{U_\mathrm{m}}{Z} \), kde Z je celková impedance obvodu.

• Rozbor úlohy

  Máme porovnat proud v obvodu s oběma kondenzátory zařazenými paralelně s proudem v obvodu ve chvíli, kdy jeden z kondenzátorů odpojíme. Oba proudy získáme pomocí Ohmova zákona pro střídavý proud a spočteme jejich poměr.

  Chceme-li získat stejný proud v obvodu s jedním kondenzátorem jako v obvodu se dvěma kondenzátory, musíme změnit velikost odporu reostatu tak, aby se celková impedance obvodu rovnala hodnotě před odpojením kondenzátoru.

• Změna proudu při odpojení jednoho z kondenzátorů

  Proud pro obvod s oběma kondenzátory zapojenými paralelně vyjádříme pomocí Ohmova zákona:

  \[I_\mathrm{m1}=\frac{U_\mathrm{m}}{Z_1}=\frac{U_\mathrm{m}}{ \sqrt{R^2+X_C^2}}=\frac{U_\mathrm{m}}{ \sqrt{R^2+ \left(\frac{1}{2 \pi f C}\right)^2}}=\frac{U_\mathrm{m}}{ \sqrt{R^2+ \left(\frac{1}{2 \pi f (C_1+C_2)}\right)^2}}=\frac{U_\mathrm{m}}{ \sqrt{R^2+ \left(\frac{1}{4 \pi f C_1}\right)^2}}\mathrm{.}\]

   

  Vyjádření proudu pro obvod, kdy jeden z kondenzátorů odpojíme, se liší pouze v tom, že dosadíme jinou kapacitu:

  \[I_\mathrm{m2}=\frac{U_\mathrm{m}}{Z_2}=\frac{U_\mathrm{m}}{ \sqrt{R^2+X_C^2}}=\frac{U_\mathrm{m}}{ \sqrt{R^2+ \left(\frac{1}{2 \pi f C}\right)^2}}=\frac{U_\mathrm{m}}{ \sqrt{R^2+ \left(\frac{1}{2 \pi f C_1}\right)^2}}\mathrm{.}\]

   

  Změnu proudu po odpojení jednoho z kondenzátorů vyjádříme poměrem mezi oběma proudy:

  \[\frac{I_\mathrm{m2}}{I_\mathrm{m1}}=\frac{\frac{U_\mathrm{m}}{ \sqrt{R^2+ \left(\frac{1}{2 \pi f C_1}\right)^2}}}{\frac{U_\mathrm{m}}{ \sqrt{R^2+ \left(\frac{1}{4 \pi f C_1}\right)^2}}}=\frac{ \sqrt{R^2+ \left(\frac{1}{4 \pi f C_1}\right)^2}}{\sqrt{R^2+ \left(\frac{1}{2 \pi f C_1}\right)^2}}. \]

• Změna velikosti odporu na reostatu

  Aby se proud po odpojení kondenzátoru rovnal proudu I_m1, musíme změnit velikost odporu reostatu. Novou hodnotu odporu označíme R_x. Napětí na zdroji je stejné pro obě zapojení. Změnou odporu reostatu musíme dosáhnout rovnosti impedancí Z₁ a Z₃ obou obvodů, a tím zajistíme i rovnost proudů:

  \[Z_3=Z_1\]

  \[\sqrt{ \left(R_\mathrm{x}\right)^2+ \left(\frac{1}{2 \pi f C_1}\right)^2}= \sqrt{R^2+ \left(\frac{1}{4 \pi f C_1}\right)^2}.\]

  Z předchozího vztahu vyjádříme hledaný odpor reostatu R_x:

  \[\left(R_\mathrm{x}\right)^2+ \left(\frac{1}{2 \pi f C_1}\right)^2=R^2+ \left(\frac{1}{4 \pi f C_1}\right)^2\]

  \[\left(R_\mathrm{x}\right)^2=R^2 + \left(\frac{1}{4 \pi f C_1}\right)^2 - \left(\frac{1}{2 \pi f C_1}\right)^2\]

  \[R_\mathrm{x}= \sqrt{R^2-\frac{3}{4}\left(\frac{1}{2 \pi f C_1}\right)^2 }.\]

• Číselné dosazení

  Změna proudu:

  \[\frac{I_\mathrm{m2}}{I_\mathrm{m1}}=\frac{ \sqrt{R^2+ \left(\frac{1}{4 \pi f C_1}\right)^2}}{\sqrt{R^2+ \left(\frac{1}{2 \pi f C_1}\right)^2}} =\frac{ \sqrt{ 240^2+ \left(\frac{1}{4 \pi \cdot 50 {\cdot} 16 \cdot 10^{-6}}\right)^2 } }{ \sqrt{240^2+ \left(\frac{1}{2 \pi \cdot 50 {\cdot} 16 \cdot 10^{-6}}\right)^2} }\,\dot{=}\,0{,}8. \]

  Velikost odporu reostatu tak, aby byl proud po odpojení jednoho z kondenzátorů stejný:

  \[R_\mathrm{x}= \sqrt{R^2-\frac{3}{4}\left(\frac{1}{2 \pi f C_1}\right)^2 }=\sqrt{240^2-\frac{3}{4}\left(\frac{1}{2 \pi \cdot 50 {\cdot} 16 \cdot 10^{-6}}\right)^2}\,\dot=167\, \mathrm \Omega. \]

  Poměr mezi odpory je:

  \[ \frac{R_\mathrm{x}}{R}= \frac{170}{240}\,\dot{=}\,0{,}7.\]

• Odpověď

  Poměr mezi proudy je přibližně: I_m2/I_m1 = 0,8. To znamená, že odpojíme-li z obvodu jeden kondenzátor, proud se zmenší asi o 20 %.

  Velikost nového odporu reostatu je přibližně: R_x = 167 Ω. Chceme-li zachovat stejný proud po odpojení jednoho z kondenzátorů, musíme zmenšit odpor na reostatu asi o 30 %.