Výkonové přizpůsobení zátěže
Úloha číslo: 309
K baterii o elektromotorickém napětí Ue a vnitřním odporu Ri je připojen spotřebič. Najděte hodnotu elektrického odporu spotřebiče, při které bude příkon spotřebiče maximální.
Poznámka: Tuto úlohu zde řešíme dvěma způsoby:
I. Nápověda 1
Uvědomte si nebo si vyhledejte, jak vypočítáme příkon spotřebiče.
I. Nápověda 2
Vyhledejte si, jak můžeme zjistit maximální hodnotu funkce pomocí derivací.
I. Rozbor
Spotřebičem (zátěží) rozumíme vnější část obvodu, tedy prvky, které jsou k baterii připojeny.
Příkon spotřebiče vypočítáme jako součin napětí na spotřebiči a proudu, který jím protéká. Napětí se podle Ohmova zákona rovná součinu odporu zátěže a proudu protékajícího zátěží. Výkon proudu si tedy můžeme vyjádřit jako součin odporu zátěže a druhé mocniny proudu procházejícího zátěží.
Z Ohmova zákona pro uzavřený obvod víme, že proud procházející obvodem se rovná podílu elektromotorického napětí na baterii a celkového odporu obvodu (součet vnitřního odporu baterie a odporu zátěže).
Tak si vyjádříme příkon baterie jako funkci odporu spotřebiče. Maximální příkon baterie určíme pomocí derivace této funkce:
Extrémy (tj. maximum nebo minimum) funkce se nacházejí v bodech, v nichž je derivace nulová nebo neexistuje. Zjistíme tedy, pro jaké hodnoty odporu R je derivace příkonu P(R) nulová.
Abychom ověřili, že nalezený odpor odpovídá maximálnímu příkonu spotřebiče, vypočítáme druhou derivaci příkonu a ověříme, že pro daný odpor je záporná.
I. Řešení s použitím derivací
Příkon spotřebiče vypočítáme jako součin napětí na spotřebiči U a proudu I, který jím protéká. Tedy:
\[P\,=\,UI\,.\]Napětí na zátěži si vyjádříme jako součin odporu zátěže a proudu, který prochází zátěží. Pro příkon zátěže tedy platí:
\[P\,=\,UI\,=\,RI^2\,.\]Z Ohmova zákona pro uzavřený obvod víme, že pro proud I procházející obvodem platí:
\[I\,=\,\frac{U_\mathrm{e}}{R_\mathrm{i}+R}\,,\]kde Ue je elektromotorické napětí zdroje, Ri je vnitřní odpor zdroje a R odpor zátěže.
Dosadíme za proud I do vztahu pro příkon P:
\[P\,=\,RI^2\,=\,\frac{RU_\mathrm{e}^2}{\left(R_\mathrm{i}+R\right)^2}\,.\]Pokud chceme najít maximální příkon spotřebiče v závislosti na odporu R, vypočítáme derivaci funkce P = P(R):
\[ \frac{\mathrm{d}P}{\mathrm{d}R}\,=\,\frac{\mathrm{d}}{\mathrm{d}R}\hspace{5px}\left(\frac{RU_e^2}{\left(R_i+R\right)^2}\right) \] \[ \frac{\mathrm{d}P}{\mathrm{d}R}\,=\, \frac{U_\mathrm{e}^2\left(R_\mathrm{i}+R\right)^2\,-\,2U_\mathrm{e}^2R\left(R_\mathrm{i}+R\right)}{\left(R_\mathrm{i}+R\right)^4}\,. \]Nyní tuto funkci položíme rovnu nule a zjistíme tak, pro která R by mohl být příkon spotřebiče maximální:
\[ \frac{U_\mathrm{e}^2\left(R_\mathrm{i}+R\right)^2\,-\,2U_\mathrm{e}^2R\left(R_\mathrm{i}+R\right)}{\left(R_\mathrm{i}+R\right)^4}\,=\,0. \]Jmenovatel zlomku je vždy kladný. Aby byl zlomek roven nule, musí být čitatel zlomku nulový. Tedy:
\[ U_\mathrm{e}^2\left(R_\mathrm{i}+R\right)^2\,-\,2U_\mathrm{e}^2R\left(R_\mathrm{i}+R\right)\,=\,0 \] \[ U_\mathrm{e}^2\left(R_\mathrm{i}+R\right)\left(R_\mathrm{i}+R-2R\right)\,=\,0.\]Protože odpor zátěže R je nezáporný, pak součet Ri + R je vždy kladný. Musí tedy platit:
\[R_\mathrm{i}\,+\,R-2R\,=\,0\] \[R=R_\mathrm{i}.\]To znamená, že maximální příkon by spotřebič mohl mít v případě, že se jeho odpor R rovná vnitřnímu odporu baterie Ri.
I. Ověření „maximálnosti“ příkonu
V minulém oddíle jsme zjistili, že funkce
\[ P\left(R\right)\,=\,\frac{RU_\mathrm{e}^2}{\left(R_\mathrm{i}+R\right)^2} \]má v bodě R = Ri nulovou derivaci, tj. bod „podezřelý z toho, že v něm má funkce maximum“.
Zda je pro tuto hodnotu odporu zátěže příkon spotřebiče maximální, zjistíme z druhé derivace funkce P(R):
\[ \frac{\mathrm{d}^2P}{\mathrm{d}R^2}\,=\, \frac{\mathrm{d}}{\mathrm{d}R}\hspace{10px}\left(\frac{\mathrm{d}P}{\mathrm{d}R}\right). \]Budeme tedy derivovat funkci, kterou jsme zderivovali již v předchozím oddíle:
\[ \frac{\mathrm{d}^2P}{\mathrm{d}R^2}\,=\, \frac{\mathrm{d}}{\mathrm{d}R}\hspace{10px} \frac{U_\mathrm{e}^2\left(R_\mathrm{i}+R\right)^2\,-\,2U_\mathrm{e}^2R\left(R_\mathrm{i}+R\right)}{\left(R_\mathrm{i}+R\right)^4}\,. \]Nejprve si ale funkci
\[ \frac{\mathrm{d}P}{\mathrm{d}R}\,=\, \frac{U_\mathrm{e}^2\left(R_\mathrm{i}+R\right)^2\,-\,2U_\mathrm{e}^2R\left(R_\mathrm{i}+R\right)}{\left(R_\mathrm{i}+R\right)^4} \]rozepíšeme jako rozdíl dvou funkcí:
\[ \frac{\mathrm{d}P}{\mathrm{d}R}\,=\, \frac{U_\mathrm{e}^2\left(R_\mathrm{i}+R\right)^2}{\left(R_\mathrm{i}+R\right)^4}\,-\,\frac{2U_\mathrm{e}^2R\left(R_\mathrm{i}+R\right)}{\left(R_\mathrm{i}+R\right)^4} \]a zlomky pokrátíme:
\[ \frac{\mathrm{d}P}{\mathrm{d}R}\,=\, \frac{U_\mathrm{e}^2}{\left(R_\mathrm{i}+R\right)^2}\,-\,\frac{2U_\mathrm{e}^2R}{\left(R_\mathrm{i}+R\right)^3}\,. \]Nyní vypočítáme druhou derivaci funkce P(R):
\[ \frac{\mathrm{d}^2P}{\mathrm{d}R^2}\,=\,\frac{\mathrm{d}}{\mathrm{d}R}\,\left[ \frac{U_\mathrm{e}^2}{\left(R_\mathrm{i}+R\right)^2}\,-\,\frac{2U_\mathrm{e}^2R}{\left(R_\mathrm{i}+R\right)^3}\right] \] \[ \frac{\mathrm{d}^2P}{\mathrm{d}R^2}\,=\, \frac{-2U_\mathrm{e}^2}{\left(R_\mathrm{i}+R\right)^3}\,-\,\frac{2U_\mathrm{e}^2\left(R_\mathrm{i}+R\right)^3-2U_\mathrm{e}^2R\cdot3\left(R_\mathrm{i}+R\right)^2}{\left(R_\mathrm{i}+R\right)^6}\,. \]Oba zlomky převedeme na společného jmenovatele (Ri + R)4:
\[ \frac{\mathrm{d}^2P}{\mathrm{d}R^2}\,=\, \frac{-2U_\mathrm{e}^2\left(R_\mathrm{i}+R\right)}{\left(R_\mathrm{i}+R\right)^4}\,-\,\frac{2U_\mathrm{e}^2\left(R_\mathrm{i}+R\right)\,-\,6U_\mathrm{e}^2R}{\left(R_\mathrm{i}+R\right)^4} \]a sečteme je:
\[ \frac{\mathrm{d}^2P}{\mathrm{d}R^2}\,=\, \frac{-2U_\mathrm{e}^2\left(R_\mathrm{i}+R\right)\,-\,2U_\mathrm{e}^2\left(R_\mathrm{i}+R\right)\,+\,6U_\mathrm{e}^2R}{\left(R_\mathrm{i}+R\right)^4}\,. \]Pro druhou derivaci funkce P(R) tak získáme rovnici:
\[ \frac{\mathrm{d}^2P}{\mathrm{d}R^2}\,=\, \frac{6U_\mathrm{e}^2R\,-\,4U_\mathrm{e}^2\left(R_\mathrm{i}+R\right)}{\left(R_\mathrm{i}+R\right)^4}\,. \]Dosadíme za odpor spotřebiče R = Ri:
\[ \frac{\mathrm{d}^2P}{\mathrm{d}R^2}\left(R=R_\mathrm{i}\right)= \frac{6U_\mathrm{e}^2R_\mathrm{i}\,-\,4U_\mathrm{e}^2\left(R_\mathrm{i}+R_\mathrm{i}\right)}{\left(R_\mathrm{i}+R_\mathrm{i}\right)^4}\,=\, \frac{6U_\mathrm{e}^2R_\mathrm{i}\,-\,4U_\mathrm{e}^2{\cdot} 2R_\mathrm{i}}{\left(2R_\mathrm{i}\right)^4} \] \[ \frac{\mathrm{d}^2P}{\mathrm{d}R^2}\left(R=R_\mathrm{i}\right)= \frac{-2U_\mathrm{e}^2R_\mathrm{i}}{16R_\mathrm{i}^4}\,=\,-\frac{U_\mathrm{e}^2}{8R_\mathrm{i}^3}\,<\,0. \]Hodnoty elektromotorického napětí a vnitřního odporu baterie jsou kladné. Proto je druhá derivace příkonu pro R = Ri záporná.
Pro odpor rezistoru R = Ri je tedy skutečně příkon baterie maximální.
II. Nápověda
Abychom se vyhnuli použití složitější matematiky, jako jsou např. derivace, budeme nejprve hledat, jaký proud musí procházet spotřebičem, aby jeho příkon při připojení na baterii byl maximální.
Vyjádřete si tedy příkon spotřebiče pomocí proudu tekoucího obvodem a parametrů baterie (jejího elektromotorického napětí a vnitřního odporu). Načrtněte si graf této závislosti.
II. Rozbor
Příkon spotřebiče se rovná součinu napětí na spotřebiči a proudu, který jím prochází. Napětí na spotřebiči získáme jako rozdíl elektromotorického napětí baterie a napětí na vnitřním odporu baterie. Po provedení výpočtů zjistíme, že příkon spotřebiče je kvadratickou funkcí proudu, který prochází obvodem. Grafem této závislosti je parabola.
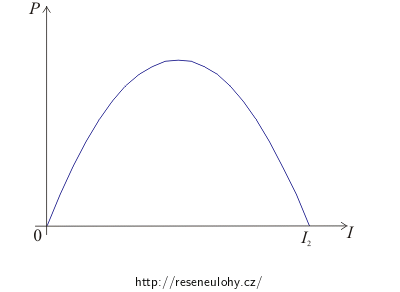
Určíme vrchol paraboly, tj. proud, pro který je příkon spotřebiče maximální. Z proudu potom určíme odpovídající odpor spotřebiče.
II. Řešení bez použití derivací
Příkon spotřebiče se rovná součinu napětí na spotřebiči a proudu, který jím prochází:
\[ P\,=\,UI. \]Napětí na spotřebiči získáme jako rozdíl elektromotorického napětí baterie a svorkového napětí (napětí na vnitřním odporu baterie):
\[ U\,=\,U_\mathrm{e}\,-\,R_\mathrm{i}I. \]Příkon spotřebiče pak vypočítáme:
\[ P\,=\,\left(U_\mathrm{e}\,-\,R_\mathrm{i}I\right)I\,=\,U_\mathrm{e}I\,-\,R_\mathrm{i}I^2. \tag{*}\]Příkon spotřebiče je tedy kvadratickou funkcí proudu.
Grafem této závislosti je parabola:

Z rovnice (*) zjistíme, pro které hodnoty proudu I je příkon spotřebiče P nulový:
\[ P\,=\,0\hspace{15px}\Rightarrow\hspace{15px}U_\mathrm{e}I\,-\,R_\mathrm{i}I^2\,=\,0 \] \[ \left(U_\mathrm{e}\,-\,R_\mathrm{i}I\right)I\,=\,0\hspace{15px}\Rightarrow\hspace{15px}I_1\,=\,0\hspace{15px}\mathrm{nebo}\hspace{15px}I_2\,=\,\frac{U_\mathrm{e}}{R_\mathrm{i}}\,. \]Z grafu vidíme, že maximálního výkonu dosáhneme, když obvodem bude protékat proud, jehož hodnota bude dvakrát menší než hodnota proudu I2. Tedy:
\[ I_\mathrm{max}\,=\,\frac{I_2}{2}\,=\,\frac{U_\mathrm{e}}{2R_\mathrm{i}}\,. \tag{1}\]Podle Ohmova zákona vypočítáme proud procházející obvodem jako podíl elektromotorického napětí a součtu odporu spotřebiče a vnitřního odporu zdroje:
\[ I\,=\,\frac{U_\mathrm{e}}{R+R_\mathrm{i}}\,. \tag{2}\]Nyní porovnáme vztahy (1) a (2) a získáme tak hodnotu odporu R, při které bude příkon spotřebiče maximální:
\[ \frac{U_\mathrm{e}}{2R_\mathrm{i}}\,=\,\frac{U_\mathrm{e}}{R+R_\mathrm{i}}\hspace{15px}\Rightarrow\hspace{15px}R\,=\,R_\mathrm{i}. \]To znamená, že maximální příkon má spotřebič v případě, že se jeho odpor R rovná vnitřnímu odporu baterie Ri.
Odpověď
Příkon spotřebiče je maximální, pokud se odpor zátěže rovná vnitřnímu odporu baterie.
Odkaz na podobnou úlohu
Zkuste vyřešit také úlohu Paúhoř elektrický, ve které se hledá maximální proud v obvodu.
Poznámka – účinnost zapojení
Účinnost elektrického obvodu η (účinnost zdroje), tedy „jak je výkonnost zapojení dobrá“, je dána vztahem:
\[ \eta\,=\,\frac{P}{P_\mathrm{z}}\,, \]kde P je příkon spotřebiče a Pz výkon zdroje.
Tento vztah můžeme dále upravit:
\[ \eta\,=\,\frac{UI}{U_\mathrm{e}I}\,=\,\frac{RI^2}{\left(R+R_\mathrm{i}\right)I^2}\,=\,\frac{R}{R+R_\mathrm{i}}\,. \]U je napětí na spotřebiči, Ue elektromotorické napětí, I proud procházející obvodem, R odpor spotřebiče a Ri vnitřní odpor zdroje.
Nyní vidíme, že pro naše řešení, kdy se odpor spotřebiče R rovná vnitřnímu odporu baterie Ri, je sice příkon spotřebiče maximální, ale účinnost tohoto zapojení je jen 50 %.
Jednoduché elektrické obvody, např. v kapesní svítilně nebo automobilu, jsou konstruovány tak, aby se dosáhlo kompromisu mezi maximální účinností a maximálním příkonem spotřebiče.
Pozn.: Funkce \( \eta(R)=\frac{R}{R+R_i} \) je rostoucí, takže účinnost elektrického obvodu je tím větší, čím vyšší je odpor R rezistoru připojeného ke zdroji.



