Reálná cívka
Úloha číslo: 795
Ke zdroji střídavého napětí s efektivní hodnotou 10 V a frekvencí 50 Hz připojíme reálnou cívku. Obvodem prochází proud o efektivní hodnotě 16 mA. Zařadíme-li do série s cívkou rezistor o odporu 470 Ω, zmenší se proud tekoucí cívkou na hodnotu 12 mA. Určete indukčnost L a odpor RL reálné cívky.
Nápověda – reálná cívka
Reálná cívka má indukčnost i odpor. Schématicky reálnou cívku znázorňujeme jako cívku spojenou sériově s rezistorem.
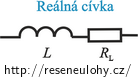
Nápověda
V zadání se mluví o dvou zapojeních — nejdříve připojíme ke zdroji reálnou cívku, poté připojíme ke zdroji reálnou cívku a rezistor. Také máme určit dvě neznámé — indukčnost a odpor cívky. Zkuste použít Ohmův zákon pro obě zapojení, tím získáte dvě rovnice pro dvě neznámé.
Nápověda – spojení reálné cívky a rezistoru
Máme-li k reálné cívce o indukčnosti L a odporu RL připojit sériově rezistor o odporu R, změní se velikost celkového odporu obvodu Rc. Jelikož se jedná o sériové zapojení rezistorů, můžeme celkový odpor Rc vyjádřit pomocí vztahu:
\[ R_\mathrm{c} = R_\mathrm{L} + R. \]Rozbor
Pomocí Ohmova zákona pro obvod se střídavým napětím vyjádříme rovnici pro výpočet napětí v obvodu s reálnou cívkou a rovnici pro výpočet napětí v obvodu, ve kterém k reálné cívce připojíme sériově rezistor. Pomocí diagramů odvodíme velikosti celkových impedancí pro jednotlivé obvody. Získáme tak dvě rovnice pro dvě neznámé, kterými jsou indukčnost a odpor cívky. Tuto soustavu vyřešíme.
Řešení
Do obvodu je zapojena reálná cívka. To znamená, že je charakterizována jak indukčností L, tak odporem RL.
Před připojením rezistoru o odporu R do obvodu z Ohmova zákona platí:
\[ U = Z_\mathrm{L} I_1, \]kde U je efektivní hodnota napětí zdroje, ZL impedance reálné cívky a I efektivní hodnota proudu v obvodu. Vyjádříme impedanci ZL reálné cívky pomocí diagramu a dosadíme do vztahu výše:
\[ Z_\mathrm{L} = \sqrt{ R_\mathrm{L}^2 + X_\mathrm{L}^2}, \] \[ U = \sqrt{ R_\mathrm{L}^2 + X_\mathrm{L}^2}\, I_1. \]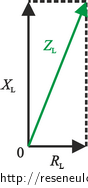
Nyní připojíme do obvodu k reálné cívce sériově rezistor o odporu R. Z Ohmova zákona pro obvod se střídavým napětím vyplývá:
\[ U = Z I_2, \]kde Z je celková impedance zapojení. Vyjádříme celkovou impedanci Z z diagramu:
\[ Z = \sqrt{ (R+R_\mathrm{L})^2 + X_\mathrm{L}^2 }\]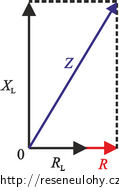
a dosadíme do Ohmova zákona pro toto zapojení:
\[ U = \sqrt{ (R+R_\mathrm{L})^2 + X_\mathrm{L}^2 }\, I_2. \]
Získali jsme dvě rovnice pro dvě neznámé, induktanci cívky XL a odpor cívky RL:
\[ U = \sqrt{ R_\mathrm{L}^2 + X_\mathrm{L}^2}\, I_1, \tag{1}\] \[ U = \sqrt{ (R+R_\mathrm{L})^2 + X_\mathrm{L}^2 }\, I_2. \tag{2}\]Rovnice upravíme a umocníme:
\[ \frac{U}{I_1} = \sqrt{ R_\mathrm{L}^2 + X_\mathrm{L}^2} \hspace{60px}\Rightarrow\qquad\left(\frac{U}{I_1}\right)^2 = R_\mathrm{L}^2 + X_\mathrm{L}^2, \] \[ \frac{U}{I_2} = \sqrt{ (R+R_\mathrm{L})^2 + X_\mathrm{L}^2 }\qquad\Rightarrow\qquad \left(\frac{U}{I_2}\right)^2 = (R+R_\mathrm{L})^2 + X_\mathrm{L}^2 \]a odečteme od sebe, abychom získali rovnici jen o jedné neznámé — odporu RL (neznámá induktance XL se odečte):
\[ \left(\frac{U}{I_1}\right)^2-\left(\frac{U}{I_2}\right)^2 = R_\mathrm{L}^2 + X_\mathrm{L}^2 - [ (R+R_\mathrm{L})^2 + X_L^2 ]. \]Rovnici upravíme:
\[ \left(\frac{U}{I_1}\right)^2-\left(\frac{U}{I_2}\right)^2 = - R^2 -2R R_\mathrm{L} \]a vyjádříme odpor cívky RL:
\[ R_\mathrm{L}= \frac{- R^2 - \left(\frac{U}{I_1}\right)^2+\left(\frac{U}{I_2}\right)^2 }{2R} = \frac{U^2}{2RI_2^2} \,-\,\frac{R}{2} \,-\, \frac{U^2}{2RI_1^2}.\]
Induktanci cívky XL vyjádříme například z následující rovnice:
\[ U = \sqrt{ R_\mathrm{L}^2 + X_\mathrm{L}^2}\, I_1, \tag{1}\] \[ \frac{U}{I_1} = \sqrt{ R_\mathrm{L}^2 + X_\mathrm{L}^2}, \] \[ \left(\frac{U}{I_1}\right)^2 = R_\mathrm{L}^2 + X_\mathrm{L}^2, \] \[ X_\mathrm{L} = \sqrt{\left(\frac{U}{I_1}\right)^2 - R_\mathrm{L}^2}. \]Dosadíme za odpor cívky RL výraz odvozený výše:
\[ X_\mathrm{L} = \sqrt{\left(\frac{U}{I_1}\right)^2 - \left(\frac{U^2}{2RI_2^2} \,-\,\frac{R}{2} \,-\, \frac{U^2}{2RI_1^2}\right)^2}. \]Vyjádříme indukčnost cívky L z poznatku, že XL = 2πfL, kde f je frekvence napětí zdroje:
\[ 2 \pi f L = \sqrt{\left(\frac{U}{I_1}\right)^2 - \left(\frac{U^2}{2RI_2^2} \,-\,\frac{R}{2} \,-\, \frac{U^2}{2RI_1^2}\right)^2 }, \] \[ L = \frac{1}{ 2 \pi f} \sqrt{\left(\frac{U}{I_1}\right)^2 - \left(\frac{U^2}{2RI_2^2} \,-\,\frac{R}{2} \,-\, \frac{U^2}{2RI_1^2}\right)^2 }. \]Zápis a číselné dosazení
U = 10 V efektivní hodnota napětí zdroje I1 = 16 mA = 0,016 A proud protékající reálnou cívkou R = 470 Ω odpor rezistoru I2 = 12 mA = 0,012 A proud protékající obvodem sériového zapojení reálné cívky a rezistoru f = 50 Hz frekvence napětí zdroje RL = ? (Ω) odpor reálné cívky L = ? (H) indukčnost cívky
\[ R_\mathrm{L}=\frac{U^2}{2RI_2^2} \,-\,\frac{R}{2} \,-\, \frac{U^2}{2RI_1^2}= \frac{10^2}{2{\cdot} 470 \cdot 0{,}012^2} \,-\,\frac{470}{2} \,-\, \frac{10^2}{2{\cdot} 470 \cdot 0{,}016^2}\,\dot=\, 88 \,\mathrm \Omega \] \[ L = \frac{1}{ 2 \pi f}\sqrt{(\frac{U}{I_1})^2 - (\frac{U^2}{2RI_2^2} \,-\,\frac{R}{2} \,-\, \frac{U^2}{2RI_1^2})^2 } =\] \[ \,\ \ = \frac{1}{ 2 \cdot \pi \cdot 50}\sqrt{(\frac{10}{0{,}016})^2 - (\frac{10^2}{2{\cdot} 470 \cdot 0{,}012^2} \,-\,\frac{470}{2} \,-\, \frac{10^2}{2{\cdot} 470 \cdot 0{,}016 ^2})^2 } \,\dot=\,2\,\mathrm H \]Odpověď
Odpor cívky má hodnotu přibližně 88 Ω a indukčnost cívky je asi 2 H.


