Kondenzátor s olejem
Úloha číslo: 88
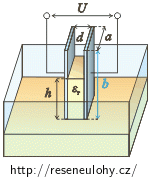
Deskový kondenzátor o rozměrech a = 10 cm, b = 15 cm a vzdálenosti desek d = 0,2 mm se dotýká hladiny oleje o relativní permitivitě εr = 2,2 a hustotě ρ = 760 kg m−3. Kondenzátor připojíme na zdroj stejnosměrného napětí U = 500 V. Olej se mezi deskami kondenzátoru zvedne do výšky h.
a) Určete kapacitu kondenzátoru.
b) Určete přírůstek energie elektrického pole kondenzátoru a přírůstek potenciální tíhové energie zvednuté části oleje, jestliže hladina oleje stoupne oproti dané hodnotě o výšku dh.
c) Vypočtěte h pro zadané rovnovážné hodnoty.
d) Určete hodnotu napětí, při kterém olej vyplní celý kondenzátor.
Rozbor:
Před připojením kondenzátoru ke zdroji je kapacita kondenzátoru přímo úměrná ploše desek a permitivitě vzduchu a nepřímo úměrná jejich vzdálenosti.
Po připojení zdroje napětí se hladina oleje mezi deskami kondenzátoru zvedne do výšky h. Kapacita kondenzátoru se zvětší, protože se zvětšila permitivita prostředí v části s olejem. Kondenzátor si nyní můžeme představit jako dva kondenzátory zapojené paralelně. Jeden kondenzátor je celý vyplněný olejem a druhý vzduchem. Celkovou kapacitu kondenzátoru získáme jako součet kapacit těchto dvou kondenzátorů.
Energie elektrického pole kondenzátoru je přímo úměrná jeho kapacitě a druhé mocnině připojeného napětí. Po připojení ke zdroji napětí se zvětší kapacita kondenzátoru, a proto se zvýší i energie jeho elektrického pole. Zajímá nás, jak se tato energie mění v závislosti na změně kapacity. Změnu energie vyjádříme pomocí derivace energie podle kapacity.
Potenciální tíhová energie oleje v kondenzátoru je přímo úměrná jeho hmotnosti a výšce těžiště nad spodní hranou kondenzátoru. Pokud se hladina oleje zvýší, zvětší se i jeho potenciální tíhová energie. Změnu této energie můžeme opět vyjádřit pomocí derivace energie tentokrát podle výšky hladiny oleje.
Aby hladina oleje stoupla, musí zdroj napětí vykonat práci, která je třeba na zvýšení potenciální tíhové energie oleje a energie elektrického pole kondenzátoru. Zároveň je tato práce přímo úměrná připojenému napětí a změně náboje na kondenzátoru. Změnu náboje můžeme dále vyjádřit pomocí změny kapacity kondenzátoru. Máme-li práci vyjádřenou těmito dvěma způsoby, můžeme vypočítat výšku hladiny oleje.
Pokud vyplní olej celý kondenzátor, pak je výška hladiny oleje stejná jako výška kondenzátoru. Napětí můžeme dopočítat ze vztahu, který jsme si vyjádřili pro výšku hladiny oleje.
a) Nápověda: Kapacita kondenzátoru
Pokud je kondenzátor z části vyplněn olejem, můžeme si ho představit jako dva kondenzátory zapojené paralelně. Jeden kondenzátor je vyplněný olejem a druhý vzduchem (Podrobnější řešení podobné situace naleznete v úloze Kondenzátor částečně vyplněný dielektrikem).
Jak spočítáme kapacitu paralelně zapojených kondenzátorů?
a) Řešení: Kapacita kondenzátoru
Před připojením ke zdroji je kondenzátor vyplněn pouze vzduchem a má kapacitu:
\[C_0\,=\,\varepsilon_0 \,\frac{ab}{d}\,.\]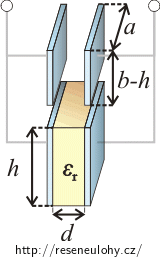
Po připojení ke zdroji se kondenzátor z části vyplní olejem. Můžeme si ho představit jako dva kondenzátory zapojené paralelně (viz obrázek). Jejich kapacita je:
\[C_{\mathrm{vzduch}}\,=\,\varepsilon_0\, \frac{a \, \left(b-h\right)}{d},\] \[C_{\mathrm{olej}}\,=\,\varepsilon_0\, \varepsilon_r \frac{a h}{d}.\]Celkovou kapacitu kondenzátoru spočteme jako součet kapacit kondenzátoru vyplněného vzduchem a kondenzátoru vyplněného olejem:
\[C\,=\,C_{\mathrm{vzduch}} \,+\, C_{\mathrm{olej}},\] \[C\,=\,\varepsilon_0 \,\frac{a \, \left(b-h\right)}{d} \,+\, \varepsilon_0 \,\varepsilon_r \frac{a h}{d}.\]Vytkneme společné členy a vzorec upravíme:
\[C\,=\,\varepsilon_0 \,\frac{a }{d}\,\left( b-h\,+\, \varepsilon_r h\right).\]Kondenzátor má tedy kapacitu:
\[C\,=\,\varepsilon_0 \frac{a }{d}\,\left( b+h\left( \varepsilon_r -1\right)\right).\]Za povšimnutí stojí, jak se tato kapacita liší od původní kapacity kondenzátoru vyplněného pouze vzduchem C0. Vnější závorku roznásobíme, aby jeden člen byl roven původní kapacitě:
\[C\,=\,\varepsilon_0 \frac{a b }{d} +\varepsilon_0 \frac{a h\left( \varepsilon_r -1\right)}{d}\,=\,C_0 + \varepsilon_0 \frac{a h\left( \varepsilon_r -1\right)}{d}.\]Druhý člen závisí lineárně na výšce h, do které vystoupí olej. Pokud olej vystoupí ještě o výšku dh, změní se kapacita kondenzátoru právě v tomto členu. Přírůstek kapacity, který označíme dC, bude:
\[\mathrm{d}C\,=\,\varepsilon_0 \frac{a \left( \varepsilon_r -1\right)}{d}\,\mathrm{d}h\,.\tag{1}\]b) Nápověda: Změny energií
Energie elektrického pole kondenzátoru E se mění v závislosti na změně jeho kapacity a tíhová potenciální energie Ep se mění se stoupající hladinou oleje.
Vypočítáme tedy derivace \(\frac{\mathrm{d}E}{\mathrm{d}C}\) a \(\frac{\mathrm{d}E_p}{\mathrm{d}h}\).
Jak se mění kapacita kondenzátoru s výškou hladiny jsme odvodili v předchozím oddíle.
Podívejte se do poznámky na konci úlohy, jak v této úloze pracujeme s derivacemi.
b) Řešení: Přírůstek energie el. pole kondenzátoru
Pro energii elektrického pole kondenzátoru platí vztah: \(E\,=\, \frac{1}{2}C U^2\,.\)Nás zajímá, jak se tato energie mění v závislosti na kapacitě. Spočítáme tedy derivaci energie podle kapacity:
\[\frac{\mathrm{d}E}{\mathrm{d}C}\,=\, \frac{1}{2} U^2.\]Kondenzátor je připojen ke stálému napětí, proto U bereme při derivování jako konstantu. Vyjádříme si změnu energie:
\[\mathrm{d}E\,=\, \frac{1}{2} U^2\mathrm{d}C.\]Dosadíme za změnu kapacity dC ze vzorce (1), který jsme si vyjádřili v řešení části a):
\[\mathrm{d}E\,=\, \frac{1}{2} U^2\varepsilon_0 \frac{a \left( \varepsilon_\mathrm{r} -1\right)\mathrm{d}h}{d}.\]Pokud hladina oleje stoupne o dh, změní se energie el. pole kondenzátoru o
\[\mathrm{d}E\,=\,\frac{a \varepsilon_0 \left( \varepsilon_\mathrm{r} -1\right)U^2}{2d}\mathrm{d}h\,. \]b) Řešení: Změna potenciální tíhové energie
Potenciální tíhovou energii spočteme pomocí vztahu
\[E_\mathrm{p}\,=\,mgH\,.\]Pozor! V tomto vzorci je H výška, ve které je těžiště tělesa! V našem případě je těžiště oleje ve výšce \(\frac{h}{2}\) a tedy pro potenciální energii platí:
\[E_\mathrm{p}\,=\,mg\,\frac{h}{2}\,=\,V \varrho g \,\frac{h}{2}\,,\tag{*}\]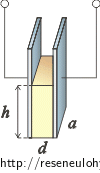
kde V je objem oleje v kondenzátoru.
Objem oleje spočítáme podle obrázku V = adh a dosadíme do vzorce (*):
\[E_\mathrm{p}\,=\,adh \varrho g \,\frac{h}{2}\,=\,\frac{1}{2}ad \varrho g \,h^2. \]Nás zajímá, jak se tato potenciální tíhová energie mění v závislosti na změně výšky oleje. Spočítáme tedy její derivaci podle výšky:
\[\frac{\mathrm{d}E_\mathrm{p}}{\mathrm{d}h}\,=\,ad \varrho g \,h. \] Změna tíhové potenciální energie je rovna: \[\mathrm{d}E_\mathrm{p}\,=\,ad \varrho gh\,\mathrm{d}h \,.\]c) Nápověda: Výpočet výšky hladiny oleje
Výšku hladiny oleje můžeme spočítat z následujícího vzorce pro práci, kterou vykoná zdroj napětí:
\[\mathrm{d}W\,=\,U \mathrm{d}Q.\]Zamyslete se nad tím, jak se projeví vykonání práce na energii kondenzátoru.
c) Řešení: Výpočet výšky hladiny h
Výšku hladiny oleje vypočítáme z práce, kterou vykoná zdroj napětí, když zvedá hladinu oleje.
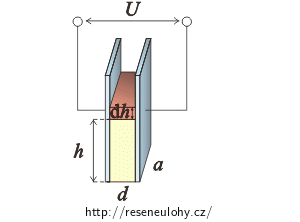
Na kondenzátoru je konstantní napětí U a hladina oleje je ve výšce h. Pokud bychom chtěli, aby hladina oleje vystoupila ještě o malý kousek dh, musí zdroj vykonat práci dW.
Protože napětí na kondenzátoru je stálé, je tato práce rovna
\[\mathrm{d}W\,=\,U \,\mathrm{d}Q\,.\]Změnu náboje při konstantním napětí můžeme vyjádřit pomocí změny kapacity kondenzátoru dQ = U dC:
\[\mathrm{d}W\,=\,U^2 \,\mathrm{d}C\,.\tag{2}\]Pokud zdroj napětí vykoná tuto práci, zvedne se hladina o dh. Tato práce se projeví změnou energie. Protože se zvýšila hladina oleje o dh, zvětšila se také jeho potenciální tíhová energie o dEp. Změnila se tím ale také kapacita kondenzátoru, a proto se zvýšila energie kondenzátoru o dE:
\[\mathrm{d}W\,=\,\mathrm{d}E_\mathrm{p}\,+\,\mathrm{d}E\,.\tag{3}\]Nyní oba vztahy (2) a (3) pro výpočet práce porovnáme:
\[U^2 \,\mathrm{d}C\,=\,\mathrm{d}E_\mathrm{p}\,+\,\mathrm{d}E.\]Jednotlivé členy jsme si vyjádřili v předchozích oddílech. Nyní je dosadíme:
\[\frac{a \varepsilon_0 \left( \varepsilon_\mathrm{r} -1\right)U^2}{d}\mathrm{d}h\,=\,\frac{a \varepsilon_0 \left( \varepsilon_\mathrm{r} -1\right)U^2}{2d}\mathrm{d}h \,+\, ad \varrho gh\,\mathrm{d}h.\]Vztah budeme upravovat, abychom vyjádřili h. Nejdříve odečteme zlomky:
\[\frac{a \varepsilon_0 \left( \varepsilon_\mathrm{r} -1\right)U^2}{2d}\mathrm{d}h\,=\, ad \varrho gh\,\mathrm{d}h\,.\tag{**}\]Zkrátíme a a dh:
\[\frac{ \varepsilon_0 \left( \varepsilon_\mathrm{r} -1\right)U^2}{2d}\,=\, d \varrho gh\]a vyjádříme výšku h, do které vystoupil olej v kondenzátoru:
\[h\,\, =\, \frac{ \varepsilon_0 \left( \varepsilon_\mathrm{r} -1\right)U^2}{2 \varrho gd^2}.\]d) Nápověda: Výpočet napětí
Jestliže olej vyplní celý kondenzátor, čemu bude rovna výška hladiny oleje?
K výpočtu napětí využijte obecného výsledku předchozí části řešení.
d) Řešení: Výpočet napětí
V předchozí části řešení Výpočet výšky hladiny oleje jsme vyjádřili výšku h, do které olej vystoupá při daném napětí:
\[h\,\,=\, \frac{ \varepsilon_0 \left( \varepsilon_\mathrm{r} -1\right)U^2}{2 \varrho gd^2}.\]Tohoto výsledku využijeme pro výpočet napětí U1, které je třeba, aby olej zaplnil celý kondenzátor.
Jestliže olej vyplní celý kondenzátor, je jeho výška h rovna výšce kondenzátoru b. Platí tedy:
\[h\,\,=\,b\,=\, \frac{ \varepsilon_0 \left( \varepsilon_\mathrm{r} -1\right)U^2_1}{2 \varrho gd^2}\,.\]
Nyní už jen vyjádříme napětí U1:
\[U^2_1\,=\, \frac{2 b\varrho gd^2}{ \varepsilon_0 \left( \varepsilon_\mathrm{r} -1\right)},\] \[U_1\,=\, \sqrt{\frac{2 b\varrho gd^2}{ \varepsilon_0 \left( \varepsilon_\mathrm{r} -1\right)}}.\]Kondenzátor musíme připojit k napětí:
\[U_1\,=\, \sqrt{\frac{2 b\varrho g}{ \varepsilon_0 \left( \varepsilon_\mathrm{r} -1\right)}}\,d\,.\]Zápis a číselný výpočet
U = 500 V
h = ? (m) a = 10 cm = 0,1 m U1 = ? (V) b = 15 cm = 0,15 m d = 0,2 mm = 0,2·10−3 m Z tabulek:
εr = 2,2 ε0 = 8,85·10−12 C2N−1m−2 ρ = 760 kg m−3 g = 9,8 m s−2
\[h\,\, =\, \frac{ \varepsilon_0 \left( \varepsilon_\mathrm{r} -1\right)U^2}{2 \varrho gd^2}\, =\, \frac{ 8{,}85 {\cdot} 10^{-12}\cdot \left( 2{,}2 -1\right)\cdot500^2}{2 {\cdot} 760 \cdot9{,}8\cdot \left(0{,}2 {\cdot} 10^{-3}\right)^2}\,\mathrm{m}\,\dot=\,4{,}46 {\cdot} 10^{-3}\,\mathrm{m}\] \[h\,\dot=\,4{,}46 \,\mathrm{mm}\] \[U_1\,=\, \sqrt{\frac{2 b\varrho g}{ \varepsilon_0 \left( \varepsilon_\mathrm{r} -1\right)}}\,d\,=\, \sqrt{\frac{2 {\cdot} 0{,}15 {\cdot} 760 \cdot9{,}8}{ 8{,}85 {\cdot} 10^{-12}\cdot \left( 2{,}2 -1\right)}}\cdot 0{,}2 {\cdot} 10^{-3}\,\mathrm{V}\] \[U_1\,\dot=\, 2\,901\,\mathrm{V}\,\dot=\, 2{,}9\,\mathrm{kV}\]Odpověď
Kondenzátor má kapacitu \(C\,=\,\varepsilon_0 \frac{a }{d}\left( b+h\left( \varepsilon_\mathrm{r} -1\right)\right)\,.\)
Jestliže se hladina oleje zvýší o dh, změní se energie elektrického pole kondenzátoru o
\[\mathrm{d}E\,=\,\frac{a \varepsilon_0 \left( \varepsilon_\mathrm{r} -1\right)U^2}{2d}\mathrm{d}h \]a potenciální tíhová energie zvednuté části oleje vzroste o
\[\mathrm{d}E_\mathrm{p}\,=\,ad \varrho gh\,\mathrm{d}h \,.\]Pro zadané hodnoty vystoupí olej do výšky
\[h\,\,=\, \frac{ \varepsilon_0 \left( \varepsilon_\mathrm{r} -1\right)U^2}{2 \varrho gd^2}\, \dot=\,4{,}46 \,\mathrm{mm}\,.\]Aby olej vyplnil celý kondenzátor, musíme ho připojit k napětí
\[U\,=\, \sqrt{\frac{2 b\varrho g}{ \varepsilon_0 \left( \varepsilon_\mathrm{r} -1\right)}}\,d\,\dot=\,2{,}9 \,\mathrm{kV}\,.\]Poznámka: Zacházení s derivacemi
V této úloze často zacházíme se zápisem derivace jako se zlomkem. Matematicky se tento postup musí zdůvodňovat. My si zde uděláme pouze „fyzikální“ představu, proč takto můžeme s derivacemi zacházet.
Změnu například potenciální tíhové energie zapisujeme na střední škole takto:
\[\mathrm{\Delta} E_\mathrm{p}\,=\, m g \, \mathrm{\Delta} h,\] \[\frac{\mathrm{\Delta} E_\mathrm{p} }{\mathrm{\Delta} h\,}=\, m g \, .\]Pokud bude přírůstek Δh velice malý (to znamená, že se limitně bude blížit nule), pak platí:
\[\lim_{\mathrm{\Delta}h \rightarrow 0}\, \frac{\mathrm{\Delta} E_\mathrm{p} }{\mathrm{\Delta} h\,}=\, \frac{\mathrm{d} E_\mathrm{p} }{\mathrm{d} h\, }.\]Pokud tedy pracujeme s malými přírůstky, můžeme derivaci „přirovnat k podílu“:
\[ \frac{\mathrm{\Delta} E_\mathrm{p} }{\mathrm{\Delta} h\,}\dot=\, \frac{\mathrm{d} E_\mathrm{p} }{\mathrm{d} h\,} \]a pracovat s ní jako se zlomkem:
\[\frac{\mathrm{d} E_\mathrm{p} }{\mathrm{d} h\,}=\, m g \, , \] \[\mathrm{d} E_\mathrm{p}\,=\, m g \, \mathrm{d} h.\]Odkaz na podobné úlohy
V úloze Dielektrický výtah zjistíte, jak by se úloha řešila, pokud by byl kondenzátor válcový.
Jak se počítá kapacita kondenzátoru s dielektrikem, naleznete také v úloze Kondenzátor částečně vyplněný dielektrikem.
Jak jinak spočítat výšku hladiny oleje
Výšku hladiny oleje jsme mohli vypočítat z rovnosti elektrické a tíhové síly stejně jako v úloze Dielektrický výtah. Výsledek by byl stejný. Můžeme to poznat ze vztahu (**) z oddílu Výpočet výšky hladiny h: \[\frac{a \varepsilon_0 \left( \varepsilon_\mathrm{r} -1\right)U^2}{2d}\mathrm{d}h\,=\, ad \varrho gh\,\mathrm{d}h.\tag{**}\]Po zkrácení dh:
\[\frac{a \varepsilon_0 \left( \varepsilon_\mathrm{r} -1\right)U^2}{2d}\,=\, ad \varrho gh.\]Na pravé straně je tíhová síla. Jelikož hmotnost oleje je m = Vρ = adhρ, je tíhová síla rovna:
\[F_\mathrm{G}\,=\,mg\,=\,adh \varrho g.\]Na levé straně je síla elektrická. V úloze Dielektrický výtah je odvozeno, že síla je rovna:
\[F\,=\,\frac{1}{2}U^2\, \frac{\mathrm{d}C}{\mathrm{d}h}\,.\]V našem případě po dosazení kapacity:
\[F\,=\,\frac{a \varepsilon_0 \left( \varepsilon_\mathrm{r} -1\right)U^2}{2d}\,.\]Obecně platí:
Jednotlivé složky síly získáme derivací potenciální energie podle příslušné souřadnice: \[F_\mathrm{x}\,=\, - \frac{\mathrm{d}E_\mathrm{p}}{\mathrm{d}x}.\] Vektor síly je tedy roven \[\vec{F}\,=\, - \mathrm{grad}E_\mathrm{p}\,.\]