Sbírka řešených úloh

Řešení obvodu Théveninovou větou

Úloha číslo: 1959

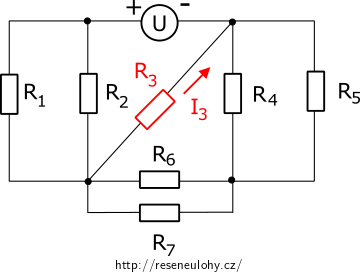
Řešte tento obvod pomocí Théveninovy věty, spočtěte proud I₃, jestliže je zadáno:

U = 20 V, R₁ = R₂ = R₃ = R₄ = R₅ = R₆ = R₇ = 5 Ω.

 

• Rozbor

  Znění Théveninovy věty: Libovolně složitý obvod lze vzhledem k libovolným dvěma svorkám nahradit obvodem skutečného zdroje napětí.

  U skutečného zdroje napětí je U₀ napětí ideálního zdroje napětí a R_i jeho vnitřní odpor. Napětí U₀ v libovolně složitém obvodu stanovíme jako napětí naprázdno na výstupních svorkách, tj. napětí, kdy je uvažovaná část obvodu vynechána. Vnitřní odpor R_i v libovolně složitém obvodu stanovíme jako odpor mezi výstupními svorkami v případě, že je zátěž odpojena, všechny zdroje napětí zkratovány, případné zdroje proudu vyřazeny.

• Postup řešení

  Našim úkolem je určit proud \(I_3\) rezistorem s odporem \(R_3\) v obvodu:

  

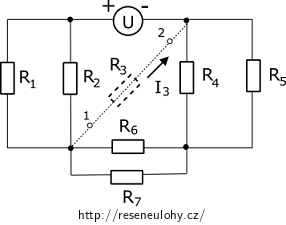
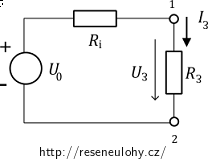
  Nakreslíme si ekvivalentní obvod dle Théveniovy věty (zůstal rezisotor R₃ a zbytek obvodu je nahrazen zdrojem s napětím U₀ s vnitřním odporem R_i).

  

   

  1. Označíme si 2 svorky (v našem případě svorky 1 a 2).

  2. Nakreslíme si ekvivalentní obvod dle Théveninovy věty.

  3. V ekvivalentním obvodu určíme vnitřní odpor R_i tak, že odpojíme zátěž (v našem případě rezistor R₃) a napětový zdrojU zkratujeme (jde o ideální zdroj).

  4. Dále musíme určit napětí ideálního zdroje U₀, který určíme tak, že odpojíme zátěž (v našem případě rezistor R₃) a určíme napětí na výstupních svorkách (svorky 1 a 2).

• 1. část řešení – vnitřní odpor R_i v ekvivalentním obvodu

  Naším úkolem je teď spočítat vnitřní odpor \(R_{i}\) zdroje, kterým nahradíme dle Théveniovy věty zbytek obvodu.

  Z postupu řešení víme, že odpor R_i spočteme tak, že odpojíme zátěž, což je v našem případě rezistor R₃ a napěťový zdroj U zkratujeme. Odpor R_i určíme vzhledem ke svorkám 1 a 2.

  

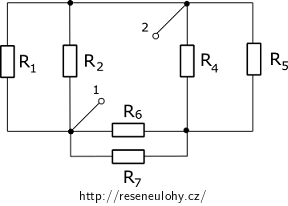
  Vidíme, že rezistory R₁ a R₂ jsou zapojeny paralelně

  \[R_\mathrm{12}\,=\, \frac{R_1R_2}{R_1+R_2}\, \,=\, \frac{5}{2}\,\,\mathrm{\Omega}\]

  a také rezistory R₄ a R₅ a také R₆ a R₇

  \[R_\mathrm{45}\,=\, \frac{R_4R_5}{R_4+R_5}\, \,=\, \frac{5}{2}\,\,\mathrm{\Omega},\] \[R_\mathrm{67}\,=\, \frac{R_6R_7}{R_6+R_7}\, \,=\, \frac{5}{2}\,\,\mathrm{\Omega}.\]

  Obvod jsme tímto zjednodušili.

  

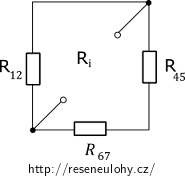
  Rezistory R₄₅ a R₆₇ jsou zapojeny sériově a k ním je připojen paralelně rezistor R₁₂. Vnitřní odpor R_i tedy je :

  \[R_\mathrm{i}\,=\, \frac{R_\mathrm{12}(R_\mathrm{45} + R_\mathrm{67})}{R_\mathrm{12}+R_\mathrm{45}+R_\mathrm{67}}\, \,=\, \frac{5}{3}\,\,\mathrm{\Omega}.\]

  Pro ty, kteří by si chtěli procvičit zapojení s rezistory nebo jsou si v tom ještě nejistí, tak doporučujeme následující úlohy.

  • Netradiční obvody 2
  • Netradiční obvody 1
  • Odpor elektrické sítě

• 2. část řešení – napětí naprázdno U₀ v ekvivalentním obvodu

  Budeme zjišťovat napětí U₀ mezi svorkami 1 a 2. To provedeme tak, že odpojíme zátěž (viz postup řešení).

  

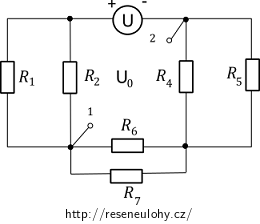
  Hledané napětí U₀ můžeme spočítat ruznými způsoby. Ten nejjednodušší asi je, že napětí U₀ spočítáme jako součet úbytku napětí na rezistorech R₄₅ a R₆₇.

  Z obvodu vidíme, že napětí naprázdno U₀ spočítáme tak, že sečteme úbytky napětí na rezistorech R₄, R₅, které jsou zapojeny paralelně a úbytky napětí na rezistorech R₆, R₇, které jsou také zapojeny paralelně. Celkový proud I v obvodu je:

  \[ I \,=\, \frac{U}{R_\mathrm{celkovy}}\,, \]

  kde \(R_\mathrm{celkovy}\) určíme jakou součet odporů tří bloků dvou paralelně zapojených rezistorů:

  \[ R_\mathrm{celkový}= R_{12} +R_{45} +R_{67} = \frac{R_1R_2}{R_1+R_2}\, + \frac{R_4R_5}{R_4+R_5}\, + \frac{R_6R_7}{R_6+R_7}\, \] \[ R_\mathrm{celkový} = \frac{15}{2}\,\, \mathrm{\Omega}. \]

  Celkový proud obvodem je

  \[ I \,=\, \frac{U}{R_\mathrm{celkový}}\, \,=\, \frac{20}{\frac{15}{2}} \,=\, \frac{8}{3}\,\, \mathrm{A}. \] \[ R_\mathrm{45} = \frac{R_4R_5}{R_4+R_5}\, \,=\, \frac{5}{2}\, \mathrm{\Omega} \] \[ R_\mathrm{67} = \frac{R_6R_7}{R_6+R_7}\, \,=\, \frac{5}{2}\, \mathrm{\Omega} \]

  Ekvivalnetní napětí naprázdno U₀ spočítáme:

  \[ U_0 \,=\, I(R_\mathrm{45} + R_\mathrm{67}) \,=\, 5\cdot\frac{8}{3}\, \, \mathrm{V} \] \[ U_0 \,=\, \frac{40}{3}\, \, \mathrm{V} \]

  

  Nyní už máme všechny hodnoty prvků v ekvivalentním obvodu určeny a můžeme dopočítat proud I₃.

  \[ I_3 \,=\, \frac{U_\mathrm{0}}{R_\mathrm{i}+R_3}\, \,=\, \frac{\frac{40}{3}}{\frac{5}{3}+5} \,\mathrm{A}, \] \[ I_3 \,=\, 2 \mathrm{A}. \]

• Odpověď

  Dle Théveninovy věty jsme si nakreslili ekvivalentní obvod. Určili jsme jeho vnitřní odpor \(R_i\) a napětí \(U_0\) \[R_\mathrm{i}\,=\, \frac{5}{3}\,\mathrm{\Omega},\qquad U_\mathrm{0}\,=\,\frac{40}{3}\,\mathrm{V}. \]

  Z ekvivalentního obvodu jsme dopočítali napětí I₃

  \[I_3\,=\, 2\,\mathrm{A}.\]