Odpor elektrické sítě

Úloha číslo: 676

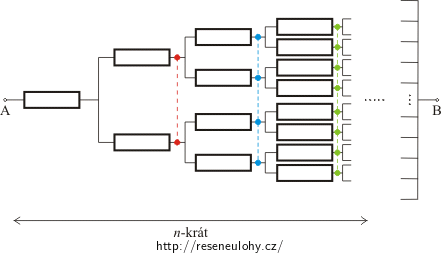
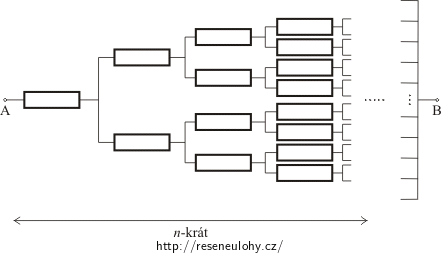
Na obrázku je zakreslena elektrická síť. Určete odpor mezi body A a B, jestliže je odpor každého rezistoru R.

Nápověda 1
Uvědomte si, jaký proud protéká mezi dvěma body o stejném potenciálu. Jak se změní celkový odpor sítě, propojíme-li tyto body vodičem?
Řešení nápovědy 1
Mezi dvěma uzly o stejném potenciálu neteče proud. Propojení těchto uzlů vodičem neovlivní celkový odpor soustavy.
Nápověda 2
Využijte pravidla zmíněného v Řešení nápovědy 1, tj. že propojením míst se stejným potenciálem nedojde ke změně odporu sítě. Najděte v zapojení místa se stejným potenciálem a překreslete síť do „přehlednější“ podoby.
Řešení nápovědy 2
Odpovídající si uzly, v nichž dochází k větvení rezistorové sítě, jsou vůči bodům A a B na stejné úrovni, a mají proto stejný potenciál. Uzly, které mají stejný potenciál, jsou v obrázku vyznačeny stejnou barvou.

Propojíme-li body o stejném potenciálu, celkový odpor sítě se nezmění. Toto propojení je v obrázku znázorněno barevnou přerušovanou čarou.

Nyní využijeme toho, že dva uzly, které jsou propojeny vodičem bez rezistoru, můžeme sloučit do jednoho uzlu. Získáme tak „přehlednější“ podobu původní elektrické sítě.
Nápověda 3
Uvědomte si, jaká pravidla platí pro počítání celkového odporu sériově a paralelně zapojených rezistorů.
Řešení nápovědy 3
Při sériovém spojení n rezistorů je celkový odpor roven součtu odporů jednotlivých rezistorů:
\[R\,=\,R_1\,+\,R_2\,+\,...\,+\,R_\mathrm{n}.\]
Při paralelním zapojení n rezistorů platí, že převrácená hodnota celkového odporu je rovna součtu převrácených hodnot odporů jednotlivých rezistorů:
\[\frac{1}{R}\,=\,\frac{1}{R_1}\,+\,\frac{1}{R_2}\,+\,...\,+\,\frac{1}{R_\mathrm{n}}.\]
Nápověda 4
Pro vyřešení úlohy je třeba umět sečíst prvních n členů geometrické posloupnosti. Vzpomeňte si na příslušný vzorec nebo si ho vyhledejte.
Řešení nápovědy 4
Součet prvních n členů geometrické posloupnosti s_n vypočítáme (pro q ≠ 1) ze vztahu
\[ s_\mathrm{n}\,=\,a_1\,\frac{1-q^\mathrm{n}}{1-q}\,, \]
kde a₁ značí první člen a q je kvocient dané geometrické posloupnosti (poměr dvou po sobě jdoucích členů).

Poznámka: Pokud by kvocient geometrické posloupnosti byl roven jedné, tj. q = 1, pak by všechny členy posloupnosti byly stejné. Tedy a_n = a₁. V takovém případě je součet prvních n členů posloupnosti roven
\[s_\mathrm{n}\,=\,n\cdot a_1\,.\]
Tento případ však v naší úloze nenastává.
Rozbor
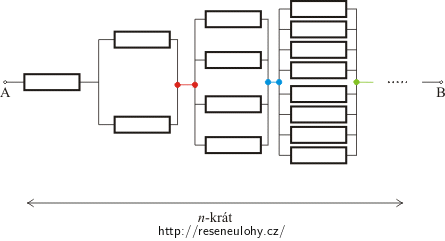
Z obrázku v zadání úlohy vidíme, že odpovídající si uzly, v nichž dochází k větvení rezistorové sítě, jsou vůči bodům A a B na stejné úrovni, a proto mají stejný potenciál. Pokud tyto body spojíme vodičem s nulovým odporem, můžeme celou síť překreslit podle následujícího obrázku, aniž bychom změnili celkový odpor sítě.

Síť je nyní složena z n sériově zapojených částí a v každé části jsou rezistory zapojeny paralelně. Počet paralelně zapojených rezistorů v k-té části elektrické sítě je 2(k − 1). V první části sítě je tedy zapojen 1 rezistor, ve druhé 2, dále 4, 8, 16, atd.

Odpor elektrické sítě mezi body A a B nyní určíme podle pravidel pro výpočet celkového odporu sériově a paralelně zapojených rezistorů.
Řešení
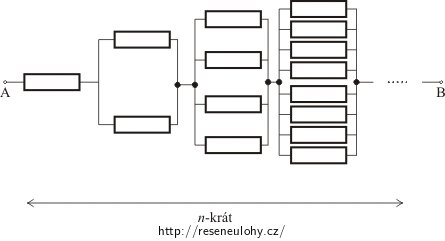
Propojením míst se stejným potenciálem můžeme schéma překreslit do přehlednější podoby (podrobněji je tato úprava popsána v oddílech Nápověda 2 a Rozbor).

Z obrázku vidíme, že síť je složena z n sériově zapojených částí a v každé části jsou rezistory zapojeny paralelně. Počet paralelně zapojených rezistorů v k-té části elektrické sítě je 2^(k − 1) (tj. v první části sítě 1 rezistor, v druhé 2, dále 4, 8, 16, ...).

Ze zadání úlohy víme, že odpor každého rezistoru v elektrické síti je R. Nyní je třeba si uvědomit, že x paralelně zapojených rezistorů má v souladu s pravidly pro spojování rezistorů odpor \(\frac{R}{x}\). Proto můžeme pro celkový odpor sítě R_AB napsat vztah:
\[ R_\mathrm{AB}\,=\,R\,+\,\frac{R}{2}\,+\,\frac{R}{4}\,+\,\frac{R}{8}\,+\,...\,+\,\frac{R}{2^\mathrm{n-1}}, \] \[ R_\mathrm{AB}\,=\,R\left(1\,+\,\frac{1}{2}\,+\,\frac{1}{4}\,+\,\frac{1}{8}\,+\,...\,+\,\frac{1}{2^\mathrm{n-1}}\right). \]
Výraz v závorce je součtem prvních n členů geometrické posloupnosti s prvním členem a₁ = 1 a kvocientem q = \(\frac{1}{2}\). Pro tento součet platí obecně vzorec
\[s_\mathrm{n}\,=\,a_1\,\frac{1-q^\mathrm{n}}{1-q}.\]
Pro naše konkrétní hodnoty je součet prvních n členů posloupnosti:
\[ s_\mathrm{n}\,=\,1\cdot\,\frac{1-\frac{1}{2}^\mathrm{n}}{1-\frac{1}{2}}\,=\,\frac{\frac{2^\mathrm{n}-1^\mathrm{n}}{2^\mathrm{n}}}{\frac{2-1}{2}}\,=\,\frac{\frac{2^\mathrm{n}-1}{2^\mathrm{n}}}{\frac{1}{2}}\,=\,\frac{2\cdot\left(2^\mathrm{n}-1\right)}{2^\mathrm{n}}\,=\,\frac{2^\mathrm{n}-1}{2^\mathrm{n-1}}. \]
Pro odpor mezi body A a B elektrické sítě tedy platí vztah:
\[ R_\mathrm{AB}\,=\,R\,\frac{2^\mathrm{n}-1}{2^\mathrm{n-1}}. \]
Odpověď
Pro odpor sítě mezi body A a B platí vztah:
\[ R_\mathrm{AB}\,=\,R\,\frac{2^\mathrm{n}-1}{2^{\mathrm{n}-1}}. \]
Odkaz na podobnou úlohu
Podobnou úlohou na řešení rezistorové sítě je také úloha Nekonečná síť rezistorů.