Sbírka řešených úloh

Kruhový bočník

Úloha číslo: 303

Miliampérmetr o vnitřním odporu 50 Ω má plnou výchylku při proudu 2,0 mA. Určete R₁, R₂ a R₃ pro kruhový bočník s rozsahy 10 mA, 50 mA a 250 mA.

• Nápověda 1

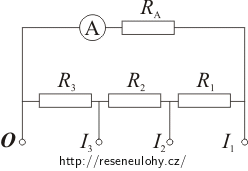
  Schéma kruhového bočníku je uvedeno na obrázku.

  

  Rozsah miliampérmetru se mění podle toho, ke kterým svorkám je bočník do obvodu připojen. V této úloze budeme ampérmetr do obvodu připojovat vždy pomocí svorky zcela vlevo (označené O) a jedné ze svorek vpravo. Pro přehlednost je u nich připsáno, jakému rozsahu ampérmetru každá svorka odpovídá.

• Nápověda 2

  Uvědomte si, jak přidaný bočník ovlivňuje proud, který prochází ampérmetrem.

• Řešení nápovědy 2

  Po zapojení bočníku k ampérmetru jím můžeme měřit proud, jehož hodnota je vyšší než hodnota, kterou dovoluje změřit měřicí přístroj.

  Při libovolném připojení bočníku budeme uvažovat, že celým obvodem prochází proud odpovídající příslušnému rozsahu. Ve všech případech bude větví s ampérmetrem stále procházet proud, při kterém má ampérmetr maximální výchylku, tedy proud 2 A. Druhou větví pak prochází proud, který určíme jako rozdíl proudu, který prochází obvodem (tj. rozsahu), a proudu procházejícího ampérmetrem.

• Rozbor

  Jestliže k miliampérmetru připojíme paralelně rezistor, tzv. bočník, pak celkový proud procházející obvodem bude větší, než proud procházející přístrojem. Stále ale bude platit, že proud procházející přímo ampérmetrem, je úměrný celkovému proudu, který prochází ampérmetrem a bočníkem dohromady. Připojením bočníku tedy zvětšíme rozsah, na kterém je miliampérmetr schopen měřit, aniž by došlo k jeho poškození.

  

  Rozsah miliampérmetru se mění podle toho, ke kterým svorkám je bočník do obvodu připojen (v této úloze budeme ampérmetr do obvodu připojovat vždy pomocí svorky O zcela vlevo a jedné ze svorek vpravo). Ze zadání úlohy známe rozsahy pro tři různá připojení:

  1. Ampérmetr je paralelně připojen ke třem rezistorům, obvodem prochází proud I₁.

  

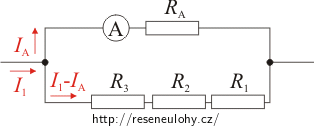
  2. Ampérmetr a rezistor R₁ jsou paralelně připojeny k rezistorům R₂ a R₃, obvodem prochází proud I₂.

  

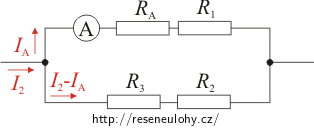
  3. Ampérmetr a rezistory R₁ a R₂ jsou paralelně připojeny k rezistoru R₃ a obvodem prochází proud I₃.

  

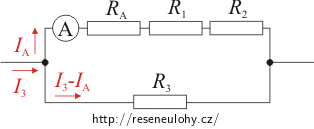
  Ve všech třech případech prochází větví s ampérmetrem proud, při kterém má ampérmetr maximální výchylku, tedy proud 2 A. Druhou (na obrázcích spodní) větví pak prochází proud, který je roven rozdílu celkového proudu procházejícího obvodem a proudu procházejícího ampérmetrem.

  Víme, že pro paralelně zapojené rezistory platí, že napětí je na všech větvích zapojení stejné, a sériově zapojenými rezistory prochází stejný proud. Díky těmto poznatkům a Ohmovu zákonu pro část obvodu si pro každé ze tří zapojení napíšeme rovnici vyjadřující rovnost napětí na paralelních větvích. Získáme tak soustavu tří rovnic o třech neznámých R₁, R₂ a R₃. Z ní vypočítáme odpory jednotlivých rezistorů bočníku.

• Řešení

  Pokud k miliampérmetru připojíme paralelně rezistor (bočník), pak celkový proud (pro jednotlivá zapojení ho označíme I₁, I₂, I₃) procházející obvodem bude větší než proud I_A procházející přístrojem. Zvýšíme tak rozsah, na kterém je miliampérmetr schopen měřit.

  Poznámka: Ve všech zapojeních bude protékat větví s měřicím přístrojem stejný proud. Pokud by přístrojem protékal proud, jehož hodnota by přesáhla hodnotu proudu, při kterém má ampérmetr plnou výchylku, pak by došlo k poškození přístroje.

  V naší úloze známe tři rozsahy pro tři různá připojení:

  1. Ampérmetr je připojen paralelně ke třem rezistorům:

  

  Obvodem bude procházet celkový proud I₁, ampérmetrem protéká proud I_A, při kterém má přístroj maximální výchylku. Druhou větví pak bude procházet proud, který se rovná rozdílu proudu I₁ a I_A.

  Napětí na paralelních větvích obvodu je konstantní. Tedy:

  \[U_\mathrm{A1}\,=\,U_\mathrm{B1}\,,\]

  kde U_A1 je napětí na větvi s ampérmetrem a U_B1 je napětí na bočníku (index 1 značí, že se zabýváme prvním zapojením).

  Tato napětí si vyjádříme pomocí Ohmova zákona pro část obvodu:

  \[R_\mathrm{A}I_\mathrm{A}\,=\,\left(R_1+R_2+R_3\right)\left(I_1-I_\mathrm{A}\right)\,,\tag{1}\]

  R_A je vnitřní odpor ampérmetru, I_A proud procházející ampérmetrem, součet odporů R₁+R₂+R₃ je celkový odpor bočníku a I₁−I_A je proud procházející bočníkem.

  2. Ampérmetr a rezistor R₁ jsou paralelně připojeny k rezistorům R₂ a R₃:

  

  Celkový proud procházející obvodem označíme I₂. Větví s ampérmetrem protéká proud I_A, druhou větví prochází proud, který se rovná rozdílu proudů I₂ a I_A.

  Rovnost napětí na paralelních větvích si opět vyjádříme pomocí Ohmova zákona:

  \[U_\mathrm{A2}\,=\,U_\mathrm{B2}\] \[\left(R_\mathrm{A}+R_1\right)I_\mathrm{A}\,=\,\left(R_2+R_3\right)\left(I_2-I_\mathrm{A}\right)\,.\tag{2}\]

  3. Ampérmetr a rezistory R₁ a R₂ jsou paralelně připojeny k rezistoru R₃:

  

  Celkový proud procházející obvodem je I₃. Větví, ve které je zapojen ampérmetr, protéká proud I_A. Druhou větví prochází proud I₃ − I_A.

  Rovnost napětí na paralelních větvích:

  \[U_\mathrm{A3}\,=\,U_\mathrm{B3}\] \[\left(R_\mathrm{A}+R_1+R_2\right)I_\mathrm{A}\,=\,R_3\left(I_3-I_\mathrm{A}\right)\,.\tag{3}\]

  Takto jsme ze tří zapojení získali tři rovnice o třech neznámých R₁, R₂ a R₃:

  \[R_\mathrm{A}I_\mathrm{A}\,=\,\left(R_1+R_2+R_3\right)\left(I_1-I_\mathrm{A}\right)\tag{1}\] \[\left(R_\mathrm{A}+R_1\right)I_\mathrm{A}\,=\,\left(R_2+R_3\right)\left(I_2-I_\mathrm{A}\right)\tag{2}\] \[\left(R_\mathrm{A}+R_1+R_2\right)I_\mathrm{A}\,=\,R_3\left(I_3-I_\mathrm{A}\right).\tag{3}\]

  Řešením této soustavy rovnic získáme hodnoty odporů rezistorů bočníku.

• Řešení soustavy rovnic a číselné dosazení

  V minulém oddíle jsme získali soustavu tří rovnic o třech neznámých R₁, R₂ a R₃:

  \[R_\mathrm{A}I_\mathrm{A}\,=\,\left(R_1+R_2+R_3\right)\left(I_1-I_\mathrm{A}\right)\tag{1}\] \[\left(R_\mathrm{A}+R_1\right)I_\mathrm{A}\,=\,\left(R_2+R_3\right)\left(I_2-I_\mathrm{A}\right)\tag{2}\] \[\left(R_\mathrm{A}+R_1+R_2\right)I_\mathrm{A}\,=\,R_3\left(I_3-I_\mathrm{A}\right).\tag{3}\]

  V zadání úlohy máme následující hodnoty:

  I_A = 2 mA, R_A = 50 Ω, I₁ = 10 mA, I₂ = 50 mA, I₃ = 250 mA.

  Tyto hodnoty dosadíme do soustavy rovnic. Pro lepší přehlednost budeme do rovnic dosazovat jen číselné hodnoty veličin bez jejich jednotek. Hodnoty proudů můžeme dosazovat v miliampérech a jednotkou hledaných odporů budou ohmy:

  \[ 50{\cdot} 2\,=\,\left(R_1+R_2+R_3\right)\left(10-2\right) \tag{1}\] \[ \left(50+R_1\right)\cdot 2\,=\,\left(R_2+R_3\right)\left(50-2\right) \tag{2}\] \[ \left(50+R_1+R_2\right)\cdot 2\,=\,R_3\left(250-2\right). \tag{3}\]

  V každé rovnici nejprve převedeme všechny neznámé na jednu stranu:

  \[ 8R_1+8R_2+8R_3\,=\,100 \tag{1}\] \[ 2R_1-48R_2-48R_3\,=\,-100 \tag{2}\] \[ 2R_1+2R_2-248R_3\,=\,-100 \tag{3}\]

  a rovnice zkrátíme:

  \[ 2R_1+2R_2+2R_3\,=\,25 \tag{1}\] \[ R_1-24R_2-24R_3\,=\,-50 \tag{2}\] \[ R_1+R_2-124R_3\,=\,-50. \tag{3}\]

  Nyní od první rovnice odečteme dvojnásobek druhé rovnice a od druhé rovnice odečteme rovnici třetí:

  \[ 50R_2+50R_3\,=\,125 \tag{1)-2(2}\] \[ -25R_2+100R_3\,=\,0. \tag{2)-(3}\]

  Rovnice opět zkrátíme:

  \[ 2R_2+2R_3\,=\,5 \tag{A}\] \[ -R_2+4R_3\,=\,0. \tag{B}\]

  Z rovnice (B) si vyjádříme R₂ a dosadíme do rovnice (A):

  \[R_2\,=\,4R_3\hspace{15px}\Rightarrow\hspace{15px}2{\cdot} 4R_3+2R_3\,=\,5 \]

  a určíme R₃:

  \[10R_3\,=\,5\hspace{15px}\Rightarrow\hspace{15px}R_3\,=\,0{,}5.\]

  Nyní dopočítáme R₂:

  \[R_2\,=\,4R_3\,=\,4{\cdot} 0{,}5\,=\,2.\]

  Z rovnice (3) víme, že:

  \[ R_1+R_2-124R_3\,=\,-50\hspace{15px}\Rightarrow\hspace{15px} R_1\,=\,124R_3-R_2-50 \] \[ R_1\,=\,124{\cdot} 0{,}5-2-50\,=\,10. \]

  Odpory rezistorů mají tedy hodnotu R₁ = 10Ω, R₂ = 2Ω a R₃ = 0,5Ω.

• Odpověď

  Rezistory kruhového bočníku mají odpory R₁ = 10 Ω, R₂ = 2 Ω, R₃ = 0,5 Ω.

• Odkaz na podobnou úlohu

  Podobnou jednodušší úlohou, která se zabývá připojováním pomocných rezistorů k měřicím přístrojům, je úloha Bočník a předřadný rezistor.

• Komentář - kruhový bočník

  Kruhový neboli Ayrtonův bočník je rozšiřitelný na větší počet rozsahů.

  Hlavní nedostatek kruhového bočníku se týká rezistorů bočníku, neboť celková přesnost tohoto zapojení je naprosto závislá na všech těchto rezistorech.

  Výhodou tohoto bočníku je, že měřidlo je trvale připojeno k bočníku a při poruše přepínače rozsahů tak nedojde k jeho přetížení.