Sbírka řešených úloh

Transformace trojúhelník - hvězda

Úloha číslo: 33

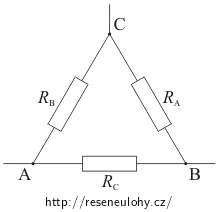
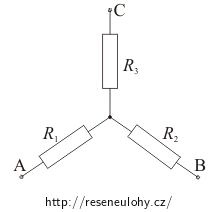
Máme rezistory R_A, R_B, R_C zapojené do „trojúhelníku“. Jak velké musí být odpory R₁, R₂, R₃ zapojené do „hvězdy“, aby se oba obvody navenek chovaly naprosto stejně (tj. pokud bychom je uzavřeli do skříňky, tak žádným způsobem nedokážeme poznat, jak zapojení vypadá)?

• Nápověda

  Aby se obě zapojení chovala stejně, musí být mezi každými dvěma body v obou zapojeních stejný celkový odpor.

• Rozbor

  Odpor mezi body A, B pro zapojení do „trojúhelníku“ se musí rovnat odporu mezi body A, B pro zapojení do „hvězdy“.

  Oba tyto odpory si vyjádříme pomocí pravidel pro počítání odporů při sériovém a paralelním zapojení.

  Totéž provedeme i pro odpory mezi body A, C a B, C.

  Dostaneme tak soustavu tří rovnic pro tři neznámé R₁, R₂, R₃ a tuto soustavu vyřešíme.

• 1. část řešení - vyjádření odporů

  Mezi každými dvěma body musí být při obou zapojeních stejný celkový odpor.

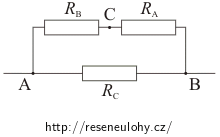
  Pro odpor mezi body A, B v zapojení do „trojúhelníku“ si můžeme obvod překreslit takto:

  

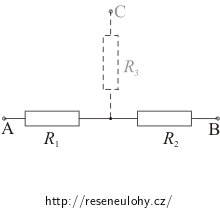
  \[\frac{1}{R_{AB}}\,=\, \frac{1}{R_C}+\frac{1}{R_B+R_A}\] \[\frac{1}{R_{AB}}\,=\, \frac{\left(R_B+R_A\right)+R_C}{R_C\left(R_B+R_A\right)}\] \[R_{AB}\,=\, \frac{R_C\left(R_A+R_B\right)}{R_A+R_B+R_C}\]

  Obvod pro odpor mezi body A, B pro „hvězdu“ můžeme nakreslit takto:

  

  \[R_{AB}\,=\, R_1+R_2\]

  Platí tedy:

  \[R_1+R_2\,=\, \frac{R_C\left(R_A+R_B\right)}{R_A+R_B+R_C}\,.\]

  Pro odpory mezi dalšími body stačí díky symetrii obvodů vždy „zaměnit“ indexy:

  \[R_1+R_3\,=\, \frac{R_B\left(R_A+R_C\right)}{R_A+R_B+R_C}\] \[R_2+R_3\,=\, \frac{R_A\left(R_B+R_C\right)}{R_A+R_B+R_C}.\]

• 2. část řešení - matematické úpravy

  V předchozím oddíle jsme získali soustavu tří rovnic pro tři neznámé R₁, R₂, R₃. Pomocí matematických úprav tuto soustavu vyřešíme:

  \[R_1+R_2\,=\, \frac{R_C\left(R_A+R_B\right)}{R_A+R_B+R_C}\tag{1}\] \[R_1+R_3\,=\, \frac{R_B\left(R_A+R_C\right)}{R_A+R_B+R_C}\tag{2}\] \[R_2+R_3\,=\, \frac{R_A\left(R_B+R_C\right)}{R_A+R_B+R_C}.\tag{3}\]

  K první rovnici přičteme druhou a třetí odečteme (1)+(2)-(3):

  \[ 2R_1\,=\, \frac{R_C\left(R_A+R_B\right)+R_B\left(R_A+R_C\right) -R_A\left(R_B+R_C\right)}{R_A+R_B+R_C} \] \[ 2R_1\,=\, \frac{R_AR_C+R_BR_C+R_AR_B+R_BR_C-R_AR_B-R_AR_C}{R_A+R_B+R_C} \] \[ 2R_1\,=\, \frac{2R_BR_C}{R_A+R_B+R_C} \] \[ R_1\,=\, \frac{R_BR_C}{R_A+R_B+R_C} \]

  Podobně spočteme odpory R₂, R₃:

  \[ R_2\,=\, \frac{R_AR_C}{R_A+R_B+R_C} \] \[ R_3\,=\, \frac{R_AR_B}{R_A+R_B+R_C} \]

  Poznámka: Pokud bychom chtěli zapojení do hvězdy nahradit zapojením do trojúhelníku, stačí si vyjádřit z uvedené soustavy rovnic R_A, R_B, R_C.

• Odpověď

  Zapojení rezistorů R_A, R_B, R_C do trojúhelníku nahradíme zapojením do hvězdy s odpory o velikosti:

  \[ R_1\,=\, \frac{R_BR_C}{R_A+R_B+R_C} \] \[ R_2\,=\, \frac{R_AR_C}{R_A+R_B+R_C} \] \[ R_3\,=\, \frac{R_AR_B}{R_A+R_B+R_C}. \]