Vznášející se vodič v magnetickém poli Země
Úloha číslo: 478
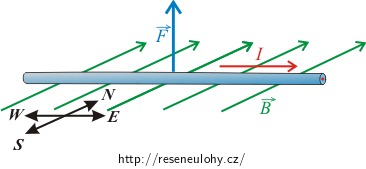
Přímý hliníkový vodič, který leží rovnoběžně s povrchem Země, má délku 0,5 m a prochází jím proud 10 A ve směru od západu k východu. Vodič se nachází v magnetickém poli Země v místě, kde je magnetická indukce rovnoběžná s povrchem Země a směřuje na sever. Její velikost je 5·10−5 T. Určete:
a) velikost a směr magnetické síly působící na vodič s proudem,
b) velikost elektrického proudu vodičem o hmotnosti 30 g, který by způsoboval vznášení vodiče v tíhovém poli.
Nápověda – Flemingovo pravidlo levé ruky
Směr magnetické síly působící na vodič s proudem v magnetickém poli určíte pomocí:
Flemingova pravidla levé ruky
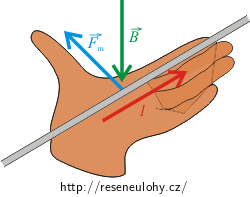
Položíme-li k vodiči levou ruku tak, aby natažené prsty ukazovaly směr proudu a magnetické indukční čáry (respektive vektor \(\vec{B}\)) vstupovaly do dlaně, ukazuje odtažený palec směr a orientaci vektoru magnetické síly \(\vec{F}_\mathrm{m}\), která působí na vodič.
Rozbor
Velikost a směr magnetické síly
Na vodič s proudem, který se nachází v magnetickém poli, působí magnetická síla, jejíž velikost závisí na velikosti magnetického pole, na proudu procházejícím vodičem a na poloze vodiče vůči magnetickým indukčním čarám. Směr magnetické síly určíme pomocí Flemingova pravidla levé ruky.
Určení velikosti elektrického proudu vodičem
Aby se mohl vodič s proudem vznášet v tíhovém poli Země, musí na něj působit síla, která bude mít stejnou velikost, ale opačný směr oproti tíhové síle působící na vodič. V našem případě působí na vodič s proudem v opačném směru magnetická síla. Vodič se bude vznášet, pokud tíhová a magnetická síla budou mít opačný směr a stejnou velikost.
Řešení a) Velikost a směr magnetické síly
Na vodič s proudem, který se nachází v magnetickém poli, působí magnetická síla o velikosti
\[F_\mathrm{m}=BIl\sin{\alpha},\]kde α je úhel, který svírá vektor magnetické indukce \(\vec{B}\) se směrem proudu ve vodiči. V našem případě (viz obrázek) platí
\[\alpha=90^\circ\,\,\,\Rightarrow\,\,\sin{\alpha} =1.\]Pro velikost magnetické síly tedy dostáváme vztah
\[F_\mathrm{m}=BIl.\]Směr vektoru magnetické síly určíme pomocí Flemingova pravidla levé ruky. Magnetická síla je kolmá na vektor magnetické indukce a na vodič s proudem a směřuje nahoru. To znamená, že mírně „nadlehčuje“ vodič.
Vidíme, že můžeme uvažovat situaci popsanou v části b), tj. že se vodič s proudem může díky magnetické síle vznášet nad povrchem Země.
Řešení b) Určení velikosti elektrického proudu
Aby se mohl vodič s proudem nadnášet v tíhovém poli Země, musí na něj působit síla, která bude mít stejnou velikost, ale opačný směr než tíhová síla \(\vec{F}_\mathrm{G}\) působící na vodič. V našem případě působí na vodič s proudem směrem nahoru magnetická síla \(\vec{F}_\mathrm{m}\) (směr jsme určili v Řešení a) pomocí Flemingova pravidla levé ruky).
Pro velikosti obou sil platí
\[F_\mathrm{m}=F_\mathrm{G}.\]Obě síly vyjádříme:
\[BIl\,\sin{\alpha}=mg,\]kde pro úhel α, který svírá vektor magnetické indukce s vodičem, v našem případě platí
\[\alpha=90^\circ\,\,\,\Rightarrow\,\,\sin{\alpha} =1.\]Dostáváme tak rovnici
\[BIl=mg,\]ze které vyjádříme hledaný elektrický proud I vodičem:
\[I=\frac{mg}{Bl}.\]Zápis a číselné dosazení
\(l\,=\,50\,\mathrm{cm}=\,0{,}50\,\mathrm{m}\) délka vodiče \(I\,=\,10\,\mathrm{A}\) proud tekoucí vodičem \(B\,=\,5{\cdot}10^{-5}\,\mathrm{T}\) magnetická indukce pole Země \(m\,=\,30\,\mathrm{g}=\,0{,}03\,\mathrm{kg}\) hmotnost vodiče \(F_\mathrm{m}\,=\,?\) velikost magnetické síly působící na vodič s proudem \(I\,=\,?\) velikost elektrického proudu vodičem, který by způsoboval vznášení vodiče v tíhovém poli Z tabulek: \(g\,=\,9{,}81\,\mathrm{ms}^{-2}\) tíhové zrychlení
\[F_\mathrm{m}=BIl=5{\cdot}10^{-5}\cdot10{\cdot}0{,}5\,\mathrm{N}=2{,}5{\cdot}10^{-4}\,\mathrm{N}\] \[I=\frac{mg}{Bl}=\frac{0{,}03{\cdot}9{,}81}{5{\cdot}10^{-5}\cdot0{,}5}\,\mathrm{A}=11\,772\,\mathrm{A}\,\dot{=}\,12\,\mathrm{kA}\]Odpověď
Magnetická síla, která působí na vodič s proudem v magnetickém poli Země, má velikost 0,25 mN a míří směrem nahoru.
Aby byl vodič s proudem nadnášen v magnetickém poli Země, musel by jím procházet proud o velikosti přibližně 12 kA.
Komentář – Poloha vodiče a různé směry proudu ve vodiči
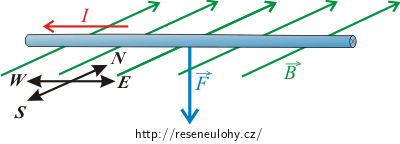
Pokud by vodičem procházel elektrický proud v opačném směru, tedy od východu na západ, magnetická síla působící na vodič s proudem by měla opačný směr, směřovala by dolů. Vodič by se v tíhovém poli nenadnášel, ale byl by naopak přitlačen směrem dolů.
Dále může být vodič, kterým prochází proud, orientován tak, že svírá s vektorem magnetické indukce úhel menší než 90°. Magnetická síla \(\vec{F}_\mathrm{m}\) působící na vodič pak bude mít menší velikost oproti případu, kdy je vodič s proudem kolmý na vektor magnetické indukce. Velikost magnetické síly je dána vztahem
\[F_\mathrm{m}=BIl\,\sin{\alpha},\]kde α je úhel, který svírá vektor magnetické indukce \(\vec{B}\) se směrem proudu ve vodiči.
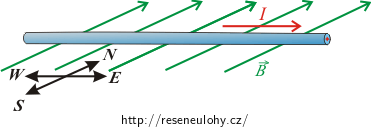
Speciální případ nastává, pokud je vodič rovnoběžný s vektorem magnetické indukce \(\vec{B}\), tj. je orientován ve směru sever-jih. Magnetická síla působící na vodič bude v tomto případě nulová.
Komentář – Realističnost proudu procházející vodičem
Pomocí vztahu pro Joulovo teplo určíme, zda-li je hodnota proudu, přibližně 12 kA, která musí hliníkovým vodičem procházet, aby byl nadnášen, vůbec reálná.
Budeme předpokládat, že vodič má kruhový průřez a určíme jeho poloměr r. Ze vztahu pro hustotu dostaneme pro poloměr vodiče vztah
\[\rho=\frac{m}{\pi r^2l}\,\,\,\Rightarrow\,\,\,r=\sqrt{\frac{m}{\rho\pi l}}.\]Dále si vyjádříme odpor R vodiče délky l o poloměru r
\[R=\frac{\rho_0 l}{\pi r^2},\]kde ρ0 je měrný elektrický odpor hliníkového vodiče, jehož hodnota je uvedena v tabulkách.
Po dosazení vztahu pro poloměr r do rovnice pro elektrický odpor dostáváme pro odpor vodiče vztah
\[R=\frac{\rho_0 l}{\pi \frac{m}{\rho\pi l}}=\frac{\rho_0\rho l^2}{m}.\]Pro Joulovo teplo, respektive Joulův výkon platí
\[P=UI=RI^2.\]Po dosazení vztahu pro odpor hliníkového vodiče dostáváme pro výkon, který se uvolní v podobě tepla, výraz
\[P=\frac{\rho_0\rho}{m}l^2I^2.\]Pro určení velikosti Joulova tepla dosadíme do vztahu pro výkon P konkrétní číselné hodnoty. Hodnoty pro hustotu hliníku ρ a měrný elektrický odpor ρ0 najdeme v tabulkách.
\[P=\frac{27{\cdot}10^{-9}\cdot2700}{0{,}03}\cdot0{,}5^2\cdot(12{\cdot}10^3)^2\,\mathrm{W}\dot{=}87{,}5\,\mathrm{kW}.\]Při průchodu proudu o velikosti přibližně 12 kA vodičem se bude uvolňovat Joulovo teplo přibližně 87,5 kW, což je velmi vysoká hodnota. Můžeme tedy předpokládat, že se vodič rozžhaví a přepálí. Nedojde tedy k jeho vznášení v magnetickém poli Země.