Sbírka řešených úloh

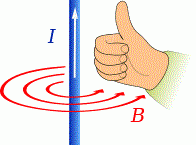
Čtyři dlouhé vodivé dráty

Úloha číslo: 2312

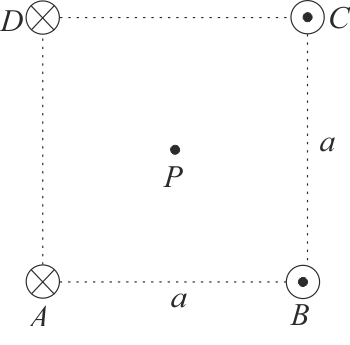
Čtyři nekonečně dlouhé rovnoběžné dráty (kolmé k obrázku) vedou stejně velké proudy I a jsou uspořádány v rozích čtverce, viz obrázek. Proudy ve vodičích označených B a C míří ven z obrázku a proudy ve vodičích A a D míří do obrázku. Jaké je magnetické pole ve středu čtverce?

• Nápověda

  Jakou velikost a směr má magnetická indukce ve vzdálenosti r od velmi dlouhého přímého vodiče?

• Řešení nápovědy

  Velikost magnetické indukce ve vzdálenosti r od dlouhého přímého vodiče je dána vztahem

  \[B=\frac{\mu}{2\pi}\frac{I}{r},\]

  kde I je proud protékající vodičem.

  Pozn.: Výpočet magnetického pole dlouhého přímého vodiče pomocí Ampérova zákona viz Magnetické pole přímého vodiče, Řešení – dlouhý přímý vodič, a pomocí Biotov-Savartova zákona viz Magnetické pole dlouhého přímého vodiče s proudem, Řešení 2.

  Magnetické indukční čáry tvoří soustředné kružnice v rovině kolmé na vodič. Jejich orientaci určíme pomocí Ampérova pravidla pravé ruky:

  Jestliže palec pravé ruky ukazuje směr elektrického proudu ve vodiči, pak pokrčené prsty ukazují orientaci magnetických indukčních čar.

  

  Zdroj obrázku: wikipedia.org

• Řešení

  Magnetická indukce je vektorová veličina, výslednice bude dána součtem příspěvků od jednotlivých vodičů:

  \[\vec{B}=\vec{B_\mathrm{A}}+\vec{B_\mathrm{B}}+\vec{B_\mathrm{C}}+\vec{B_\mathrm{D}}.\tag{1}\]

  Velikost magnetické indukce v okolí velmi dlouhého přímého vodiče závisí na velikosti proudu ve vodiči a vzdálenosti od vodiče. Všemi vodiči protéká stejný proud I. Zajímá nás magnetické pole uprostřed čtverce, tj. v místě, které je od všech vodičů stejně vzdáleno. Velikost příspěvků magnetické indukce od všech vodičů bude stejná:

  \[B_\mathrm{A}=B_\mathrm{B}=B_\mathrm{C}=B_\mathrm{D}.\]

  Velikost příspěvku od jednoho vodiče vyjádříme ze vztahu zmíněném v Řešení nápovědy:

  \[B=\frac{\mu}{2\pi}\frac{I}{r}.\]

  Vzdálenost r určíme pomocí Pythagorovy věty, viz obrázek:

  \[r^2=\left(\frac{a}{2}\right)^2+\left(\frac{a}{2}\right)^2 \Rightarrow r=\frac{\sqrt{2}}{2}a.\]

  

  \[B_A=\frac{\mu}{2\pi}\frac{I}{r}=\frac{\mu}{2\pi}\frac{I}{\frac{\sqrt{2}}{2}a}=\frac{\mu}{\pi}\frac{I}{\sqrt{2}a}.\tag{2}\]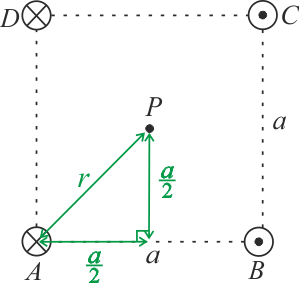

  Použitím Ampérova pravidla pravé ruky zjistíme směry jednotlivých příspěvků (viz Nápověda). Vidíme, že vektor magnetické indukce od vodiče A se rovná vektoru magnetické indukce od vodiče C, stejné platí pro vodiče B a D.

  

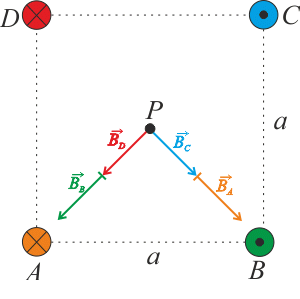
  Pozn.: Z důvodu přehlednosti jsou vektory zakresleny za sebou, aby byl patrný jejich součet. Nicméně všechny čtyři vektory odpovídají magnetické indukci v bodě \(P\):

  \[\vec{B_\mathrm{A}}=\vec{B_\mathrm{C}},\] \[\vec{B_\mathrm{B}}=\vec{B_\mathrm{D}}.\]

  Díky poslednímu poznatku můžeme upravit vztah (1):

  \[\vec{B}=2\vec{B_\mathrm{A}}+2\vec{B_\mathrm{B}},\] \[\vec{B}=2(\vec{B_\mathrm{A}}+\vec{B_\mathrm{B}}).\]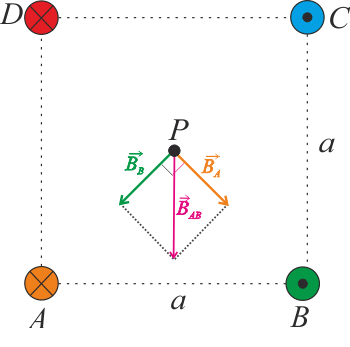

  

  Pro spočítání velikosti vektorového součtu \(\vec{B_\mathrm{A}}+\vec{B_\mathrm{B}}\) využijeme Pythagorovu větu:

  \[B=2\sqrt{B_\mathrm{A}^2+B_\mathrm{B}^2},\] \[B=2\sqrt{2B_\mathrm{A}^2},\] \[B=2\sqrt{2}B_\mathrm{A}.\]

  Do posledního vztahu dosadíme (2) a dostaneme

  \[B=2\sqrt{2}\frac{\mu}{\pi}\frac{I}{\sqrt{2}a}=2\frac{\mu}{\pi}\frac{I}{a}.\]

• Odpověď

  Výsledná magnetická indukce uprostřed čtverce bude mít směr, který ukazuje následující obrázek, a velikost

  \[B=2\frac{\mu}{\pi}\frac{I}{a}.\]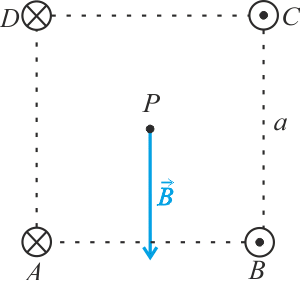

  

• Dynamický prvek

  Následující aplet nám zobrazuje vektory magnetické indukce od jednotlivých vodičů a jejich výslednici (označena \(B_\mathrm{V}\)). Bodem \(E\) můžeme pomocí myši libovolně hýbat.

  Úkoly pro práci s apletem

  1. Posouvejte bodem E a sledujte závislost velikostí příspěvků na vzdálenostech od vodičů. Sledujte závislosti směrů příspěvků na poloze bodu E.
  2. Posouvejte bodem E po osách stran čtverce a sledujte, zda má výslednice nějaký konkrétní směr. Vysvětlete, proč tomu tak je.
  3. Rozmyslete si, ve kterém místě bude platit \(\vec{B_\mathrm{D}}=\vec{B_\mathrm{C}}\). Správnost ověřte pomocí apletu.
  4. Nastavte bod E do středu čtverce a porovnejte, zda-li výslednice odpovídá řešení této úlohy.
  5. Zkuste nalézt místo, ve kterém bude výslednice magnetické indukce nulová. Pokud takové místo nenajdete, zdůvodněte, proč ho nelze najít.