Rotující disk
Úloha číslo: 2310
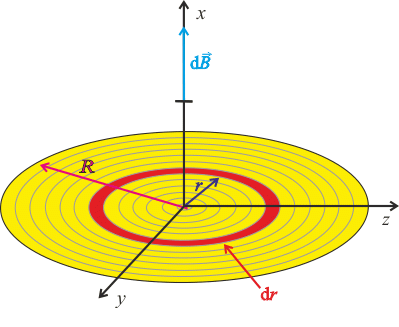
Kruhový disk s poloměrem R s konstantní nábojovou hustotou \(\sigma\) rotuje s úhlovou rychlostí \(\omega\). Určete velikost magnetické indukce na ose disku.
Nápověda
Využijme poznatků z úlohy Magnetické pole kruhového závitu, kde je vyjádřena magnetická indukce na ose kruhového závitu jako
\[B=\frac{\mu_0}{2}\, \frac{I r^2}{\left({r^2+x^2}\right)^{\frac{3}{2}}},\]kde \(r\) je poloměr závitu a \(x\) je vzdálenost od středu na ose závitu. Magnetická indukce míří ve směru osy závitu.
Vztah, který jsme si zde napsali, platí pro kruhový závit s proudem. V našem případě jednak nemáme kruhový závit (máme kruhový disk) a hlavně není řečeno, že by diskem tekl nějaký proud.
Zamyslete se nad tím, jak bychom mohli využít kruhový závit pro případ kruhového disku, a také nad tím, kde je skrytý proud v našem případě rotujícího disku.
Řešení
Rotující disk s nábojem je vlastně to samé jako nerotující disk s proudem (viz nápověda). Disk rozsekáme na kruhové smyčky a výslednou magnetickou indukci naintegrujeme přes všechny tyto smyčky.
Elementární příspěvek magnetické indukce od kruhového závitu (smyčky) s poloměrem r ve vzdálenosti \(x\) na ose závitu je (viz nápověda)
\[B=\frac{\mu_0}{2}\, \frac{I r^2}{\left({r^2+x^2}\right)^{\frac{3}{2}}},\]kde \(r\) je poloměr závitu a \(x\) je vzdálenost od středu na ose závitu. Magnetická indukce míří ve směru osy závitu.
Jednotlivé příspěvky od kruhových závitů budou přispívat k magnetické indukci
\[\mathrm{d}B=\frac{\mu_0}{2}\, \frac{ r^2}{\left({r^2+x^2}\right)^{\frac{3}{2}}}\mathrm{d}I.\tag{1}\]Nyní vyjádříme proud procházející elementárním závitem:
\[\mathrm{d}I=\frac{\mathrm{d}Q}{t}.\]Náboj dQ, který projde jedním závitem během jedné otáčky, je úměrný ploše závitu:
\[\mathrm{d}Q=\sigma \mathrm{d}S=\sigma 2\pi r \mathrm{d}r.\]Dobu jedné otáčky, tj. periody T, vyjádříme pomocí úhlové frekvence ω
\[t=T=\frac{2\pi}{\omega}.\]Spojením posledních tří vztahů dostaneme
\[\mathrm{d}I=\omega \sigma r \mathrm{d}r.\]Poslední vztah dosaďme do (1):
\[\mathrm{d}B=\frac{\mu_0}{2}\frac{\omega \sigma r^3 \mathrm{d} r} {(r^2+x^2)^{\frac{3}{2}}}.\]Sečtením (integrací) příspěvků od všech závitů získáme výslednou magnetickou indukci:
\[B=\int_0^R \frac{\mu_0}{2}\frac{\omega \sigma r^3 \mathrm{d} r} {(r^2+x^2)^{\frac{3}{2}}}=\frac{\mu_0 \omega \sigma}{2}\int_0^R \frac{ r^3 \mathrm{d} r} {(r^2+x^2)^{\frac{3}{2}}}. \]Integrál budeme řešit pomocí substituce:
\[r^2+x^2=a, \\ 2r\mathrm{d}r=\mathrm{d}a.\] \[B=\frac{\mu_0 \omega \sigma}{2}\int_{x^2}^{R^2+x^2} \frac{ (a-x^2) \mathrm{d} a} {2a^{\frac{3}{2}}}.\]Rozdělíme integrál na dva a spočteme:
\[B=\frac{\mu_0 \omega \sigma}{4}\left(\int_{x^2}^{R^2+x^2} \frac{ a } {a^{\frac{3}{2}}}\mathrm{d} a - \int_{x^2}^{R^2+x^2} \frac{ x^2 } {a^{\frac{3}{2}}}\mathrm{d} a \right),\] \[B=\frac{\mu_0 \omega \sigma}{4}\left(\int_{x^2}^{R^2+x^2} a^{-\frac{1}{2}}\mathrm{d} a - \int_{x^2}^{R^2+x^2} { x^2 } a^{-\frac{3}{2}}\mathrm{d} a \right),\] \[B=\frac{\mu_0 \omega \sigma}{4}\left(\Big[2 a^{\frac{1}{2}} \Big]_{x^2}^{R^2+x^2}- \Big[-2x^2a^{-\frac{1}{2}} \Big]_{x^2}^{R^2+x^2} \right).\]Zbývá dosadit meze a upravit:
\[B=\frac{\mu_0 \omega \sigma}{2}\left(\Big[ a^{\frac{1}{2}} \Big]_{x^2}^{R^2+x^2}+ x^2\Big[a^{-\frac{1}{2}} \Big]_{x^2}^{R^2+x^2} \right),\] \[B=\frac{\mu_0 \omega \sigma}{2}\left(\frac{2x^2 +R^2}{\sqrt{x^2+R^2}} -2x\right).\]Pozn.: V případě, že nechcete integrál řešit „ručně“, využijte výpočetní techniky, např. Wolfram Alpha.
Vyšlo nám, že magnetická indukce je úměrná rychlosti otáčení (úhlové rychlosti) a proudové hustotě, což jsme očekávali.
Speciální případ kdy \(x=0\) je řešen v oddíle Speciální případ.
Nyní se ještě zamysleme, jaká bude velikost magnetické indukce pro případ, že budeme daleko od rotujícího disku (\(x \to \infty\)). Očekáváme, že magnetická indukce v nekonečnu bude nulová, ověřme výpočtem:
\[\lim_{x\to\infty}\frac{\mu_0 \omega \sigma}{2}\left(\frac{2x^2 +R^2}{\sqrt{x^2+R^2}} -2x\right), \] \[\frac{\mu_0 \omega \sigma}{2}\lim_{x\to\infty}\frac{2x^2 +R^2-2x\sqrt{x^2+R^2}}{\sqrt{x^2+R^2}},\] \[\frac{\mu_0 \omega \sigma}{2}\lim_{x\to\infty}2\frac{x^2 -x\sqrt{x^2+R^2}}{\sqrt{x^2+R^2}}+\frac{R^2}{\sqrt{x^2+R^2}},\] \[\frac{\mu_0 \omega \sigma}{2}\lim_{x\to\infty}2\frac{(x^2 -x\sqrt{x^2+R^2})(x^2 +x\sqrt{x^2+R^2})}{\sqrt{x^2+R^2}(x^2 +x\sqrt{x^2+R^2})}+\frac{R^2}{\sqrt{x^2+R^2}},\] \[\frac{\mu_0 \omega \sigma}{2}\lim_{x\to\infty}2\frac{-x^2R^2}{x^2\sqrt{x^2+R^2}+x^3 +xR^2}+\frac{R^2}{\sqrt{x^2+R^2}}=0\space\mathrm{T}.\]Odpověď
Magnetická indukce na ose nabitého rotujícího disku ve vzdálenosti \(x\) od disku má velikost
\[B=\frac{\mu_0 \omega \sigma}{2}\left(\frac{2x^2 +R^2}{\sqrt{x^2+R^2}} -2x\right).\]Speciální případ – Magnetické pole ve středu disku
Připomeňme, že magnetická indukce ve středu kruhového závitu má velikost
\[B=\frac{\mu_0}{2}\frac{I}{R},\]kde I je proud v závitu a R je poloměr závitu.
Tohoto poznatku využijeme a kruhový disk „rozřežeme“ na kruhové závity (viz obrázek) a vyjádříme elementární příspěvek magnetické indukce od každého ze závitů. Výsledné magnetické pole získáme sečtením (integrací) příspěvků od všech závitů.
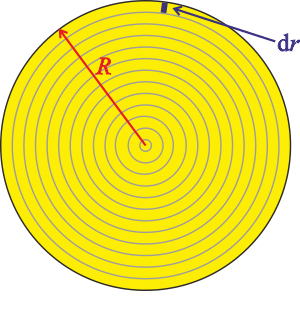
Elementární příspěvek magnetické indukce od závitu s poloměrem r má velikost
\[\mathrm{d}B=\frac{\mu_0}{2}\frac{\mathrm{d}I}{r}\tag{2}\]a všechny mají směr kolmý na disk. Nyní vyjádříme proud procházející tímto elementárním závitem:
\[\mathrm{d}I=\frac{\mathrm{d}Q}{t}.\]Náboj, který projde jedním závitem během jedné otáčky, je úměrný ploše závitu:
\[\mathrm{d}Q=\sigma \mathrm{d}S=\sigma 2\pi r \mathrm{d}r.\]Doba jedné otáčky se rovná periodě T a lze ji vyjádřit pomocí kruhové frekvence ω:
\[t=T=\frac{2\pi}{\omega}.\]Spojením posledních tří vztahů dostaneme
\[\mathrm{d}I=\omega \sigma r \mathrm{d}r.\]Poslední vztah dosaďme do (2):
\[\mathrm{d}B=\frac{\mu_0}{2}\frac{\omega \sigma r \mathrm{d}r}{r}=\frac{\mu_0 \omega \sigma }{2} \mathrm{d}r.\]Sečtením (integrací) příspěvků od všech závitů získáme výslednou magnetickou indukci:
\[B=\int_0^R \frac{\mu_0 \omega \sigma }{2} \mathrm{d}r = \frac{\mu_0 \omega \sigma }{2} \int_0^R 1\mathrm{d}r=\frac{1}{2}\mu_0 \omega \sigma R. \]Výsledek získaný tímto přímým výpočtem srovnejme s magnetickým polem na ose disku (viz výše) pro případ \(x=0\). Vidíme, že se výsledky shodují.