Sbírka řešených úloh

Magnetické pole dlouhého přímého vodiče s proudem

Úloha číslo: 472

• Nápověda 1

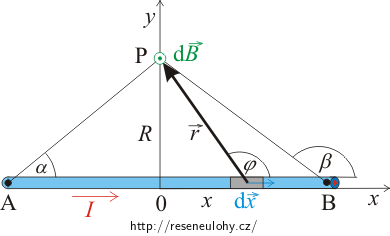
  Nakreslete si obrázek přímého vodiče s proudem a zvolte si libovolný bod P ve vzdálenosti R od vodiče. Vodič rozdělte na malé části. Každá část vodiče přispívá v bodě P k magnetickému poli. Celková magnetická indukce v bodě P je rovna součtu všech příspěvků od jednotlivých částí vodiče. Zvolíme-li dílky na vodiči velmi malé, výslednou magnetickou indukci určíme integrací přes všechny dílčí magnetické indukce od jednotlivých částí vodiče.

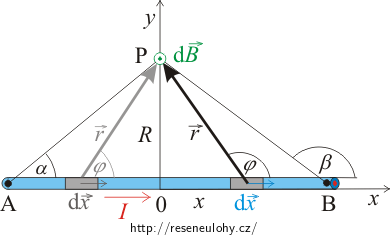
  Nakreslete si do obrázku, kterým směrem míří příspěvky od několika částí vodiče, a určete směr celkové magnetické indukce.

• Řešení nápovědy

  Na obrázku je znázorněn vodič s proudem, jehož koncové body jsme označili A a B. Polohy koncových bodů A a B vzhledem k bodu P jsou určeny úhly α a β.

  

  Počátek souřadnicové osy se nachází v patě kolmice spuštěné z bodu P na vodič (resp. na přímku, ve které vodič leží). Každý element vodiče přispívá k magnetické indukci v bodě P hodnotou magnetické indukce \(\mathrm{d}\vec{B}\), jež je dána vztahem

  \[\mathrm{d}\vec{B} = \frac{\mu_\mathrm{0}}{4\pi}\, \frac{I\, \mathrm{d}\vec{x}\times \vec{r}}{r^{3}}.\]

  Směr vektoru \(\mathrm{d}\vec{B}\) je určen pravidlem pravé ruky. Směr všech příspěvků je totožný a na obrázku míří k nám. Proto i výsledný vektor magnetické indukce \(\vec{B}\) míří k nám.

  Celková velikost magnetické indukce v bodě P od vodiče pak bude dána integrálem přes všechny příspěvky, tj. přes všechny „kousky“ vodiče.

• Nápověda 2

  Jak bylo uvedeno v Nápovědě 1, rozdělíme si celý vodič na velmi malé části. Každá z těchto částí bude přispívat v bodě P k celkovému magnetickému poli. Celkovou magnetickou indukci v bodě P určíme integrací přes příspěvky dB k magnetické indukci v bodě P.

  Naším úkolem je vyjádřit všechny proměnné, které se mění, pokud se pohybujeme podél vodiče, pomocí jedné z nich. Nejjednodušší integrál dostaneme, pokud jako tuto proměnnou zvolíme měnící se úhel mezi spojnicí jednotlivých částí vodiče s bodem P a vodičem s proudem. Rozmyslete si, které další proměnné vystupující ve vyjádření velikosti příspěvku dB se mění, pokud se pohybujeme podél vodiče. Tyto proměnné si pak vyjádřete pomocí úhlu, přes jehož velikost budeme integrovat.

• Řešení nápovědy – Vyjádření proměnných

  Na obrázku je znázorněn vodič s proudem, jehož koncové body jsme označili A a B. Jak bylo uvedeno v nápovědě, integrál bude mít nejjednodušší tvar, pokud integrační proměnnou bude měnící se úhel, který svírá vektor \(\vec{r}\) s vektorem \(\mathrm{d}\vec{x}\). Maximální a minimální hodnoty, které může hodnota úhlu nabývat, jsou úhly α a β koncových bodů A, B vzhledem k bodu P.

  

  Při integraci podél vodiče se mění r, x a úhel φ. Všechny tyto proměnné vyjádříme pomocí proměnné φ (viz obrázek). Pro vzdálenost r platí

  \[r=\frac{R}{\sin{\varphi}}.\]

  Tento vztah je patrnější, pokud si posunete vektor \(\vec{r}\) do levé části obrázku. Dále platí

  \[x=\frac{R}{tg(\pi -\varphi)}=R\,\mathrm{cotg}\,(\pi -\varphi)=-R\,\mathrm{cotg}\,\varphi\]

  a derivováním získáme

  \[\mathrm{d}x=\frac{R}{\sin^2{\varphi}}\,\mathrm{d}\varphi.\]

• Rozbor

  Velikost magnetické indukce v libovolném bodě P v okolí přímého vodiče s proudem určíme pomocí Biotova-Savartova zákona.

  Budeme uvažovat příspěvky od jednotlivých částí přímého vodiče k magnetické indukci v bodě P. Celková velikost magnetické indukce v bodě P pak bude dána integrálem přes všechny příspěvky vodiče.

  Pro získání velikosti magnetické indukce v bodě P od nekonečně dlouhého přímého vodiče jen posuneme krajní body vodiče A a B do nekonečna.

• Řešení 1

  Příspěvky \(\mathrm{d}\vec{B}\) od jednotlivých částí přímého vodiče s proudem určíme pomocí Biotova-Savartova zákona, jehož tvar je

  \[\mathrm{d}\vec{B} = \frac{\mu_\mathrm{0}}{4\pi}\, \frac{I\, \mathrm{d}\vec{x}\times \vec{r}}{r^{3}}.\]

  Pro velikost vektorového součinu platí

  \[|\mathrm{d}\vec{x}\times\vec{r}|=\mathrm{d}x\,r\,\sin{\varphi},\]

  kde úhel φ je úhel mezi vektory \(\mathrm{d}\vec{x}\) a \(\vec{r}\).

  V nápovědě jsme zdůvodnili, že všechny příspěvky mají stejný směr, proto výslednou velikost magnetické indukce získáme integrací velikosti příspěvků dB:

  \[B=\int_\mathrm{A}^\mathrm{B} \mathrm{d}B = \frac{\mu_\mathrm{0}}{4\pi}\, \int_\mathrm{A}^\mathrm{B}\frac{I\, \mathrm{d}x\,r\,\sin{\varphi}}{r^{3}}=\frac{\mu_\mathrm{0}}{4\pi}\,I\int_\mathrm{A}^{B}\frac{\sin{\varphi}}{r^{2}}\,\mathrm{d}x.\tag{1}\]

  Při integraci podél vodiče se mění r, x a úhel φ. Všechny tyto proměnné vyjádříme pomocí proměnné φ (viz obrázek). Pro vzdálenost r platí

  \[r=\frac{R}{\sin{\varphi}}.\]

  Tento vztah je patrnější, pokud si posunete vektor \(\vec{r}\) do levé části obrázku. Dále platí

  \[x=\frac{R}{\mathrm{tg}\,{(\pi -\varphi)}}=R\,\mathrm{cotg}\,{(\pi -\varphi)}=-R\,\mathrm{cotg}\,{\varphi}\]

  a derivováním získáme

  \[\mathrm{d}x=\frac{R}{\sin^2{\varphi}}\,\mathrm{d}\varphi.\]

  

  Vyjádřené proměnné dosadíme do vztahu (1)

  \[B= \frac{\mu_\mathrm{0}}{4\pi}\,I \int_\alpha^\beta \frac{R}{\sin^2{\varphi}}\,\frac{\sin^2{\varphi}}{R^2}\sin{\varphi}\,\mathrm{d}\varphi.\]

  Po úpravě získáváme integrál

  \[B= \frac{\mu_\mathrm{0}}{4\pi}\,\frac{I}{R} \int_\alpha^\beta \sin{\varphi}\,\mathrm{d}\varphi.\]

  Výraz pro výslednou magnetickou indukci zintegrujeme a dosadíme příslušné meze:

  \[B= \frac{\mu_\mathrm{0}}{4\pi}\,\frac{I}{R}\,[-\cos{\varphi}]_\alpha^\beta,\] \[B= \frac{\mu_\mathrm{0}}{4\pi}\,\frac{I}{R}\,(\cos{\alpha}-\cos{\beta}).\]

  Dostali jsme tak vztah pro magnetickou indukci v obecném bodě P v okolí přímého vodiče s proudem konečné délky.

  V případě přímého nekonečně dlouhého vodiče posuneme krajní body vodiče A a B do nekonečna. To znamená, že α = 0° a β = 180°:

  \[B= \frac{\mu_\mathrm{0}}{4\pi}\,\frac{I}{R}\,(\cos\,0^{\circ}-\cos\,180^{\circ})=\frac{\mu_\mathrm{0}}{4\pi}\,\frac{I}{R}\,\left(1-(-1)\right).\]

  Pro velikost magnetické indukce v bodě P od nekonečně dlouhého vodiče pak dostáváme známý vztah

  \[B= \frac{\mu_\mathrm{0}}{2\pi}\,\frac{I}{R}.\]

• Řešení 2

  Velikost výsledné magnetické indukce můžeme také určit z Biotova-Savartova zákona pomocí integrace přes jiné proměnné. Ukážeme si, jak určit vztah pro velikost magnetické indukce v bodě P od nekonečně dlouhého přímého vodiče s proudem pomocí integrace přes proměnnou x.

  Uvažujeme nekonečně dlouhý přímý vodiče s proudem, jehož celou délku si rozdělíme na nekonečně mnoho částí, viz obrázek.

  

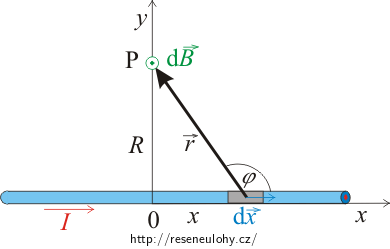
  Pro velikost magnetické indukce v bodě P platí rovnice (1) odvozená v Řešení 1, kam jsme dosadili integrační meze pro proměnnou x a uvážili, že stačí integrovat přes polovinu vodiče:

  \[B=\int_{-\infty}^\infty \mathrm{d}B=2\int_0^\infty \mathrm{d}B = \frac{\mu_oI}{2\pi}\, \int_0^\infty\frac{\sin {\varphi}\, \mathrm{d}x}{r^{2}}.\tag{2}\]

  Proměnné r, x a úhel φ v této rovnici jsou mezi sebou vázány vztahy, které jsou zřejmé z obrázku. Tentokrát vyjádříme r a φ pomocí x:

  \[r=\sqrt{x^2+R^2},\] \[\sin{\varphi}=\frac{R}{\sqrt{x^2+R^2}}.\]

  Tyto vztahy dosadíme do rovnice (2)

  \[B=\frac{\mu_\mathrm{0}I}{2\pi}\, \int_0^\infty \frac{R}{\sqrt{x^2+R^2}^{3}}\,\mathrm{d}x\]

  a integrací dostaneme

  \[B=\frac{\mu_\mathrm{0}I}{2\pi}\,\left[\frac{x}{R\sqrt{x^2+R^2}}\right]_0^\infty=\frac{\mu_\mathrm{0}I}{2\pi R},\]

  což je vztah pro velikost magnetické indukce od nekonečně dlouhého přímého vodiče s proudem, který jsme chtěli odvodit.

  Poznámka: Při vyjadřování proměnných musíme dbát na to, abychom správně vyjádřili nejen jejich velikosti, ale i znaménka.

• Výpočet integrálu

  Pro zjednodušení zápisu budeme integrál ve vztahu pro velikost magnetické indukce B počítat samostatně jako neurčitý integrál. Označíme si ho J.

  \[B=\frac{\mu_\mathrm{0}I}{2\pi}\, \int_0^\infty \frac{R}{\sqrt{x^2+R^2}^{3}}\,\mathrm{d}x,\] \[J=\int \frac{R}{\sqrt{x^2+R^2}^{3}}\,\mathrm{d}x.\]

  Pro výpočet integrálu J použijeme substituci:

  \[z=1+\frac{R^2}{x^2},\] \[\mathrm{d}z=\frac{-2R^2}{x^3}\,\mathrm{d}x.\]

  Ve jmenovateli vytkneme z odmocniny ve jmenovateli x. Tím upravíme integrovaný výraz tak, abychom mohli použít zvolenou substituci:

  \[J=\int \frac{R}{\left(x\sqrt{1+\frac{R^2}{x^2}}\right)^{3}}\,\mathrm{d}x=\int \frac{R}{x^3}\,\frac{\mathrm{d}x}{\left(\sqrt{1+\frac{R^2}{x^2}}\right)^{3}}.\]

  Po dosazení a integrování dostáváme

  \[J=\int-\frac{R}{2R^2}\,\frac{\mathrm{d}z}{\left(\sqrt{z}\right)^{3}}= \frac{1}{R}\,\frac{1}{\sqrt{z}}+c.\]

  Za proměnnou z, dosadíme ze substituce:

  \[J=\frac{1}{R\sqrt{1+\frac{R^2}{x^2}}}+c\]

  a upravíme vynásobením výrazem x/x:

  \[J= \frac{x}{Rx\sqrt{1+\frac{R^2}{x^2}}}+c= \frac{x}{R\sqrt{x^2+R^2}}+c.\]

  Dostali jsme tak integovaný výraz, jehož hodnotu určíme dosazením příslušných mezí:

  \[J=\left[\frac{x}{R\sqrt{x^2+R^2}}+c\right]_0^\infty=\frac{1}{R}.\]

  Pozn.: Pokud by byl vodič konečné délky, bude výpočet stejný, pouze bychom v jeho závěru dosadili jiné meze do integrálu.

• Odpověď

  Odvodili jsme vztah pro velikost magnetické indukce v libovolném bodě P ve vzdálenosti R od dlouhého přímého vodiče s proudem konečné délky. Pro velikost magnetické indukce v bodě P platí

  \[B= \frac{\mu_\mathrm{0}}{4\pi}\,\frac{I}{R}\,(\cos{\alpha}-\cos{\beta}).\]

  Speciálním případem je vodič nekonečné délky, kdy jsme koncové body vodiče posunuly do nekonečna. Pro velikost magnetické indukce v bodě P ve vzdálenosti R od nekonečně dlouhého vodiče s proudem platí vztah

  \[B= \frac{\mu_\mathrm{0}}{2\pi}\,\frac{I}{R}.\]