Tenký kovový proužek
Úloha číslo: 2308
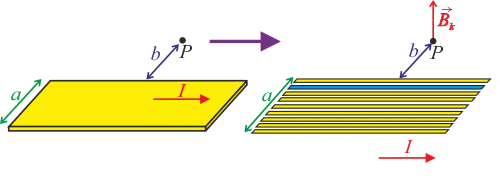
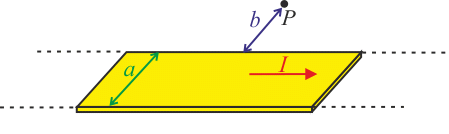
Uvažujme nekonečně dlouhý tenký proužek kovu šířky a. Proužkem protéká homogenní proud I, jehož směr je dán obrázkem. Nalezněte magnetické pole v bodě P, který leží v rovině proužku a je od něj vzdálen b.
Nápověda
Velikost magnetického pole ve vzdálenosti r od dlouhého tenkého vodiče je dána vztahem
\[B=\frac{\mu}{2\pi}\frac{I}{r},\]kde I je proud protékající vodičem. Směr magnetického pole je dán Ampérovým pravidlem pravé ruky.
Jak bychom mohli tohoto poznatku využít v této úloze?
Řešení

Jak bylo zmíněno v řešení nápovědy, tenký proužek kovu „rozřežeme“ na nekonečně mnoho tenkých přímých vodičů. Uvědomme si, že směry příspěvků od jednotlivých vodičů jsou stejné. Pomocí Ampérova pravidla pravé ruky zjistíme, že směr je kolmý na proužek a orientovaný ve směru nahoru.
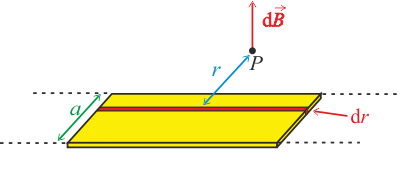
Situaci z předchozího obrázku zakreslíme i v řezu.
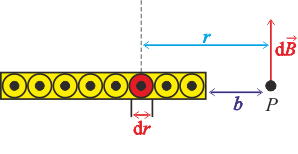
Příspěvek k magnetické indukci od jednoho z vodičů ve vzdálenosti r od bodu P je
\[\mathrm{d}B=\frac{\mu}{2\pi}\frac{\mathrm{d}I}{r}.\]Proud je v kovovém proužku homogenně rozmístěn. Proud v infinitezimálně tenkém proužku vyjádříme jako
\[\mathrm{d}I=\frac{I\mathrm{d}r}{a}.\]Spojením posledních dvou vztahů dostaneme velikost příspěvku \(\mathrm{d}B\):
\[\mathrm{d}B=\frac{\mu}{2\pi r}\frac{I\mathrm{d}r}{a}.\]Nasčítáním příspěvků (integrací) od všech „přímých vodičů“ získáme celkovou magnetickou indukci:
\[B=\int_\mathrm{b}^\mathrm{b+a}\frac{I \mu }{2\pi a }\frac{1}{r}\mathrm{d}r,\] \[B=\frac{I \mu }{2\pi a}\int_\mathrm{b}^\mathrm{b+a}\frac{1}{r}\mathrm{d}r,\] \[B=\frac{I \mu }{2\pi a}\Big[\ln r\Big]_\mathrm{b}^\mathrm{b+a},\] \[B=\frac{I \mu }{2\pi a }\ln \frac{b+a}{b}=\frac{I \mu }{2\pi a }\ln \left(1+\frac{a}{b}\right).\]Výsledný směr magnetické indukce bude kolmý na proužek a bude mířit nahoru.
Odpověď
Výsledné magnetické pole v bodě P je \(\frac{I \mu }{2\pi a }\ln \left(1+\frac{a}{b}\right). \) Výsledný směr magnetické indukce bude kolmý na proužek a bude mířit nahoru.
Komentář − limitní případ
Zamysleme se nad speciálním případem, kdy by šířka a kovového proužku byla velmi malá neboli \(a \to 0\). V takovém případě se tenký kovový proužek bude chovat jako tenký přímý vodič, pro který platí \(B_\mathrm{vodic}=\frac{\mu}{2\pi}\frac{I}{b}\). Správnost úvahy ověřme výpočtem limity:
\[B_\mathrm{vodic}=\lim_{a\to 0}\frac{I \mu }{2\pi a }\ln \left(1+\frac{a}{b}\right)=\frac{I \mu }{2\pi b}\lim_{a\to 0}\frac{\ln \left(1+\frac{a}{b}\right)}{\frac{a}{b}}=\frac{\mu}{2\pi}\frac{I}{b}.\]Pro vyřešení této limity jsme mohli využít tabulkové limity \(\lim_{x \to 0}\frac{\ln(1+x)}{x}\) nebo l’Hospitalovo pravidlo.