Řešení obvodu metodou lineární superpozice
Úloha číslo: 1958
Řešte tento obvod pomocí metody lineární superpozice. Spočtěte napětí \(U_Z\) a proud \(I_Z\), jestliže víte:
\(U_{01}\) = 15 V, \(U_{02}\) = 30 V, \(R_{1}\) = 60 Ω, \(R_{2}\) = 30 Ω, \(R_{3}\) = 40 Ω, \(R_{Z}\) = 60 Ω a \(I_{01}\) = 1 A.
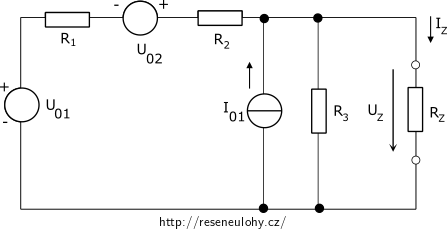
Rozbor
Metoda lineární superpozice vyjadřuje závislost mezi příčinou (působení zdrojů napětí a proudu v obvodu) a následkem (napětí a proud vzniklý v uvažovaném prvku v obvodu). Platí, že účinek součtu příčin je roven součtu následků jednotlivých příčin působících samostatně (= tzv. princip superpozice). Metodu lze použít pouze v obvodech s lineárními prvky.
Pokud tedy působí v lineárním elektrickém obvodu několik zdrojů současně, můžeme určovat napětí (nebo proud) na libovolném prvku jako součet příslušných napětí (proudů) vyvolaných jednotlivými zdroji samostatně. Necháme tedy zapojený vždy jen jeden zdroj napětí nebo proudu a stanovíme napětí (proud) na uvažovaném prvku. Ostatní zdroje napětí zkratujeme (případně nahradíme jejich vnitřními odpory) a zdroje proudu vyřadíme. To provedeme postupně pro každý zdroj.
Poznámka: U lineárních obvodů platí superpozice jen pro napětí a proud. Vztahy pro výkon jsou v těchto obvodech kvadratické (\(P=RI^2\), \( P=\frac{U^2}{R}\)), a proto pro tyto veličiny metoda lineární superpozice obecně neplatí.
Postup řešení
Naším úkolem je spočítat napětí \(U_Z\) a proud \(I_Z\).
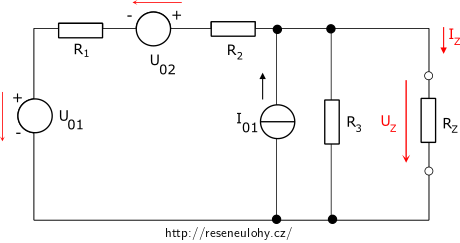
1. Vyznačíme polaritu jednotlivých zdrojů.
2. Vypočteme napětí nebo proud na uvažovaném prvku při působení jednoho zdroje, ostatních zdroje napětí nahradíme zkratem, případně nahradíme jejich vnitřním odporem, a vyřadíme zdroje proudu.
3. Bod 2 provedeme postupně pro každý zdroj.
4. Výsledné napětí nebo proud na uvažovaném prvku jsou pak dány algebraickým součtem všech dílčích napětí nebo proudů.
1. část řešení – zdroj U01
Nejprve uvažujme napětí pouze U01. To znamená, že zdroj U02 nahradíme zkratem (jedná se o ideální zdroj bez vnitřního odporu). Proudový zdroj I01 vyřadíme. Obvod tedy vypadá takto:
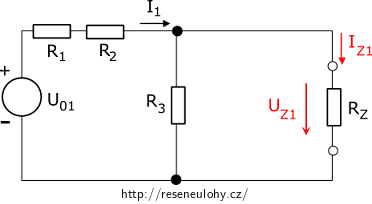
V tomto obvodu jsou rezistory R3 a RZ zapojeny paralelně a k ním jsou sériově zapojeny odpory R1 a R2. Nejdříve spočítáme celkový odpor paralelního zapojení rezistorů R3 a RZ:
\[R_\mathrm{3Z}\,=\, \frac{R_3R_Z}{R_3+R_Z}\, \,=\, \frac{40{\cdot}60}{40+60}\,\,\mathrm{\Omega},\] \[R_\mathrm{3Z}\,=\, 24 \,\mathrm{\Omega}. \]Dále spočítáme proud I1 podle Ohmova zákona (ve jmenovateli je dosazen celkový odpor obvodu):
\[I_1\,=\, \frac{U_\mathrm{01}}{R_\mathrm{3Z}+R_1+R_2}\,\,=\, \frac{15}{24+60+30}\,\mathrm{A},\] \[I_1\,=\, \frac{5}{38}\,\,\mathrm{A} \dot{=}\,0{,}13\,\mathrm{A}.\]Napětí UZ1 vypočteme podle Ohmova zákona jako součin odporu paralelního zapojení a celkového proudu jako:
\[U_\mathrm{Z1}\,=\,R_\mathrm{3Z}I_1 \, \,=\, 24\frac{5}{38}\,\,\mathrm{V}, \] \[U_\mathrm{Z1}\,=\,\frac{60}{19}\,\,\mathrm{V} \dot{=}\,3{,}16\,\mathrm{V}. \]Protože rezistory s odpory R3 a RZ jsou zapojeny paralelně, je na nich stejné napětí, které je stejné jako napětí UZ1 na celém paralelním zapojení.
2. část řešení – zdroj U02
Teď uvažujme jen zdroj U02, zdroj U01 nahradíme zkratem. (jedná se o ideální zdroj bez vnitřního odporu) a proudový zdroj I01 vyřadíme.
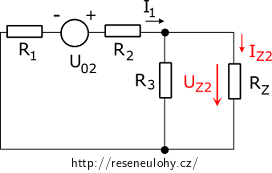
V tomto obvodu jsou opět rezistory R3 a RZ zapojeny paralelně. Z předchozího oddílu máme R3Z vypočítaný. \[R_\mathrm{3Z}\,=\, \frac{R_3R_Z}{R_3+R_Z}\,=\, 24 \,\mathrm{\Omega} \]
A stejně jako v minulém oddíle spočítáme proud I1podle Ohmova zákona
\[I_1\,=\, \frac{U_\mathrm{02}}{R_\mathrm{3Z}+R_1+R_2}\,\,=\, \frac{30}{24+60+30}\,\mathrm{A},\] \[I_1\,=\, \frac{5}{19}\,\,\mathrm{A} \dot{=}\,0{,}26\,\mathrm{A} \]a napětí UZ2:
\[U_\mathrm{Z2}\,=\,R_\mathrm{3Z}I_1 \, \,=\, 24\frac{5}{19}\,\,\mathrm{V}, \] \[U_\mathrm{Z2}\,=\,\frac{120}{19}\,\,\mathrm{V} \dot{=}\,6{,}3\,\mathrm{V}. \]3. část řešení – zdroj I01
Teď uvažujme jen proudový zdroj I01, to znamená, že zdroje U01 a U02 nahradíme zkratem (jedná se o ideální zdroje bez vnitřního odporu).
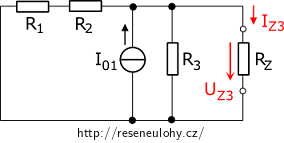
V tomto obvodu jsou opět rezistory R3 a RZ zapojeny paralelně s celkovým odporem R3Z (viz předchozí výpočet)
\[R_\mathrm{3Z}=\frac{R_3R_Z}{R_3+R_Z}= 24 \,\mathrm{\Omega} \]a k nim je paralně připojena větev s sériově zapojenými rezistory R1 a R1. Celkový odpor zapojení je tedy
\[R_C = \frac{(R_1+R_2)R_{3Z}}{R_1+R_2+R_{3Z}}\]a napětí UZ3 tedy podle Ohmova zákona vypočteme jako:
\[U_\mathrm{Z3}\,=\,I_\mathrm{01}\frac{(R_1+R_2)R_\mathrm{3Z}}{(R_1+R_2)+R_\mathrm{3Z}}, \] \[U_\mathrm{Z3}= 1\cdot\frac{(60+30)24}{(60+30)+24}\,\,\mathrm{V}=\frac{360}{19}\,\,\mathrm{V} \dot{=}\,19\,\mathrm{V}. \]4. část řešení – napětí UZ a proud IZ
Nyní už máme spočítaná napětí UZ1, UZ2 a UZ3 vzhledem k tomu, že v obvodu se už nevyskutuje další zdroj, tak výsledné napětí UZ je dáno součtem UZ1, UZ2 a UZ3
\[U_\mathrm{Z}\,=\, U_\mathrm{Z1}\ + U_\mathrm{Z2}\ + U_\mathrm{Z3}\ \,=\,\frac{540}{19}\,\,\mathrm{V} \dot{=}\,29\,\mathrm{V}. \]Proud IZ určíme pomocí Ohmova zákona
\[ I_Z \,=\,\frac{U_Z}{R_Z}\, \,=\, \frac{9}{19}\,\, \mathrm{A} \dot{=}\,0{,}47\,\mathrm{A}.\]Odpověď
Postupně jsme vypočítali napětí \(U_{Z1}\), \(U_{Z2}\) a \(U_{Z3}\) tak, že jsme v obvodu uvažovali vždy pouze jeden zdroj
\[U_\mathrm{Z1}\,=\, \frac{60}{19}\,\, \mathrm{V},\qquad \ U_\mathrm{Z2}\,=\,\frac{120}{19}\, \mathrm{V},\qquad \ \ U_\mathrm{Z3}\,=\,\frac{360}{19}\, \mathrm{V}. \]Výsledné napětí \(U_{Z3}\) je součtem napětí \(U_{Z1}\), \(U_{Z2}\) a \(U_{Z3}\)
\[U_\mathrm{Z}\,=\, \frac{540}{19}\,\,\mathrm{V} \dot{=}\,28{,}42\,\mathrm{V}. \]Proud \(I_{Z}\) je určen pomocí Ohmova zákona
\[ I_Z \,=\,\frac{U_Z}{R_Z}\, \,=\, \frac{9}{19}\,\, \mathrm{A} \dot{=}\,0{,}47\,\mathrm{A}.\]

