Sbírka řešených úloh

Čtverec

Úloha číslo: 268

• a) Nápověda: Intenzita a potenciál el. pole

  Všechny náboje mají stejnou velikost a vzdálenost od místa, kde zjišťujeme intenzitu elektrického pole. Co bude tedy platit pro velikosti vektorů intenzit elektrického pole?

  Potenciál ve středu čtverce získáme součtem potenciálů elektrických polí, které vytvářejí jednotlivé náboje v rozích čtverce.

• a) Řešení: Intenzita el. pole

  Velikost elektrické intenzity je přímo úměrná velikosti náboje, který elektrické pole vytváří, a nepřímo úměrná druhé mocnině vzdálenosti náboje od místa, kde intenzitu zjišťujeme.

  Všechny náboje jsou stejně velké a mají stejnou vzdálenost od středu čtverce. Velikost elektrické intenzity polí jednotlivých nábojů je tedy stejná.

  Směr vektoru elektrické intenzity je stejný jako směr elektrické síly, která by v daném místě působila na kladný náboj. Protože náboje ve vrcholech čtverce jsou kladné, míří intenzita vždy směrem od nich. Nakreslíme-li si obrázek, je vidět, že vektory el. intenzity polí nábojů v protilehlých rozích čtverce mají opačný směr. Protože mají zároveň vždy stejnou velikost, tak se navzájem odečtou.

  

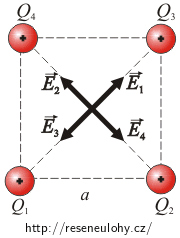
  Celková intenzita elektrického pole je tedy rovna nule.

• a) Rozbor: Potenciál ve středu čtverce

  Celkový potenciál elektrického pole ve středu čtverce získáme součtem potenciálů elektrických polí jednotlivých nábojů. Potenciál elektrického pole bodového náboje je přímo úměrný velikosti bodového náboje a nepřímo úměrný vzdálenosti náboje od místa, kde potenciál zjišťujeme. Protože jsou všechny náboje stejně velké a mají zároveň stejnou vzdálenost od středu čtverce, tak ve středu čtverce vytvářejí elektrická pole o stejném potenciálu.

• a) Řešení: Potenciál ve středu čtverce

  Celkový potenciál ve středu čtverce je roven součtu potenciálů polí jednotlivých nábojů.

  Pro elektrický potenciál pole bodového náboje Q ve vzdálenosti r od něj platí obecný vztah:

  \[\varphi\,=\, \frac{1}{4 \pi \varepsilon_0} \frac{Q}{r}\,. \]

  Protože všechny náboje mají stejnou velikost a jsou od středu čtverce ve stejné vzdálenosti, je potenciál vždy stejný. Náboje jsou od středu vzdáleny polovinu úhlopříčky, což je \(\frac{a \sqrt{2}}{2}\). Potenciál jednotlivých polí je tedy roven:

  \[\varphi\,=\, \frac{1}{4 \pi \varepsilon_0}\, \frac{Q}{\frac{a \sqrt{2}}{2}}\,=\,\frac{1}{4 \pi \varepsilon_0}\, \frac{2Q }{a\sqrt{2} }\,.\]

  Čitatele i jmenovatele vynásobíme odmocninou ze dvou, abychom odstranili odmocninu ve jmenovateli:

  \[\varphi\,=\,\frac{1}{4 \pi \varepsilon_0}\, \frac{2\sqrt{2}Q }{2a }\,=\,\frac{1}{4 \pi \varepsilon_0}\, \frac{\sqrt{2}Q }{a }.\]

  Celkový potenciál získáme součtem potenciálů jednotlivých polí, tj. jako čtyřnásobek potenciálu pole jednoho náboje:

  \[\varphi_\mathrm{c}\,=\,4 \varphi\,=\, \frac{1}{4 \pi \varepsilon_0}\, \frac{4\sqrt{2}Q}{a}.\]

• b) Nápověda

  Jaké síly působí na náboj v rohu čtverce?

  Nakreslete si obrázek a určete výslednici těchto sil.

• b) Obrázek působících sil

  

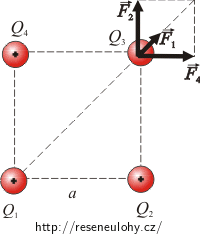
• b) Rozbor

  Abychom vypočítali velikost náboje q, který musíme umístit do středu čtverce tak, aby nepůsobila na náboje v rozích žádná síla, musíme nejdříve zjistit, jaká je výsledná elektrická síla, kterou na vybraný náboj působí ostatní náboje v rozích čtverce.

  Na náboj v jednom rohu čtverce působí náboje umístěné v ostatních třech rozích čtverce odpudivou elektrickou silou. Velikost těchto sil vypočítáme z Coulombova zákona. Výslednou sílu, která na náboj v rohu působí, získáme vektorovým součtem jednotlivých sil.

  Do středu čtverce musíme umístit takový náboj, který bude působit stejně velkou silou, ale opačného směru. Protože náboj ve středu čtverce musí okolní náboje přitahovat, bude mít záporné znaménko. Velikost tohoto náboje získáme z Coulombova zákona.

• b) Řešení: Velikost náboje q

  Velikosti sil budeme počítat z Coulombova zákona: \[F\,=\, k \, \frac{Q^2}{r^2}.\]

  Na obrázku jsou zakresleny pouze síly, které působí na náboj Q₃. U ostatních nábojů je situace analogická.

  

  Náboje Q₂ a Q₄ jsou od náboje Q₃ vzdáleny a, proto působí na náboj stejně velkou silou:

  \[F_2\,=\,F_4\,=\, k \, \frac{Q^2}{a^2}.\]

  Vzdálenost náboje Q₁ od Q₃ je \(a\sqrt{2}\), což je úhlopříčka ve čtverci o straně a:

  \[F_1\,=\, k \, \frac{Q^2}{\left( \sqrt{2} a \right)^2},\] \[F_1\,=\, k \, \frac{Q^2}{2 a^2}.\]

  Výslednici sil získáme vektorovým součtem. Nejdříve sečteme síly \(\vec{F}_2\) a \(\vec{F}_4\). Výslednice těchto dvou sil je úhlopříčkou ve čtverci o straně F₂ a její velikost je tedy:

  

  \[F_{24}\,=\,\sqrt{2}F_2\,,\] \[F_{24}\,=\,\sqrt{2}k \, \frac{Q^2}{a^2}.\]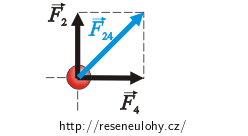

  Výslednou sílu \(\vec{F}\) získáme vektorovým součtem sil \(\vec{F}_{24}\) a \(\vec{F}_1\), jejichž velikost jsme si vyjádřili:

  

  \[F\,=\,F_{24}+F_1,\] \[F\,=\,\sqrt{2}k \, \frac{Q^2}{a^2}\,+\,k \, \frac{Q^2}{2 a^2},\] \[F\,=\,k \, \frac{Q^2}{a^2}\,\left(\sqrt{2}\,+\, \frac{1}{2 }\right).\tag{*}\]

  Do středu čtverce musíme umístit náboj, který bude působit silou \(\vec{F^,}\) stejně velkou, ale opačného směru než je síla \(\vec{F}\). Její velikost vypočítáme z Coulombova zákona:

  

  \[F^,\,=\, k \,\frac{Q q}{\left(\frac{a\sqrt{2}}{2}\right)^2}\,,\]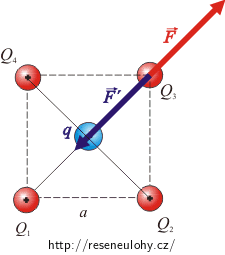

  kde \(\frac{a\sqrt{2}}{2}\) je polovina úhlopříčky.

  Jmenovatele zlomku upravíme:

  \[F^,\,=\, k \,\frac{Q q}{\frac{a^2 2}{4}}\,=\, k \,\frac{Q q}{\frac{a^2}{2}},\] \[F^,\,=\, k \,\frac{2Q q}{a^2}.\tag{**}\]

  Nyní porovnáme vyjádření sil F a F ^, ze vzorce (*) a (**):

  \[k \,\frac{2Q q}{a^2}\,=\, \,k \, \frac{Q^2}{a^2}\,\left(\sqrt{2}\,+\, \frac{1}{2 }\right).\]

  Zkrátíme a vyjádříme velikost hledaného náboje q:

  \[2q \,=\,Q\,\left(\sqrt{2}\,+\, \frac{1}{2 }\right), \] \[2q \,=\,Q\,\left(\frac{2\sqrt{2}\,+\, 1}{2 }\right), \] \[ q\,=\,Q\,\left(\frac{2\sqrt{2}\,+\, 1}{4 }\right). \]

• Odpověď

  Ve středu čtverce je intenzita elektrického pole rovna nule.

  Potenciál ve středu čtverce je roven

  \[\varphi_\mathrm{c}\,=\,4 \varphi\,=\, \frac{1}{4 \pi \varepsilon_0}\, \frac{4\sqrt{2}Q}{a}\,.\]

  Aby na náboje v rozích čtverce nepůsobila žádná síla, musíme do středu čtverce umístit záporný náboj o velikosti

  \[ q\,=\,Q\,\left(\frac{2\sqrt{2}\,+\, 1}{4 }\right)\,. \]