Sbírka řešených úloh

Jednofázový elektromotor

Úloha číslo: 234

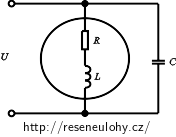
Jednofázový elektromotor je připojen na síť 230 V, 50 Hz. Při proudu 4 A má příkon 750 W. Určete kapacitu paralelně připojeného kondenzátoru, kterým se účiník upraví na hodnotu cos φ = 1. (Motor považujte za sériovou kombinaci indukčnosti a odporu tak, jak je naznačeno na obrázku.)

• Nápověda

  Upravení účiníku na hodnotu cos φ = 1 znamená, že má být celkový proud ve fázi s napětím na celém zapojení — mezi proudem a napětím má být nulový fázový posun.

• Nápověda – fázorové diagramy

  Zapojení je sériovo–paralelní, a proto bude fázorový diagram vypadat jinak než u jednoduchého sériového zapojení.

  Kreslení fázorových diagramů pro sériové zapojení je detailně popsáno v úloze Sériový RLC obvod.

  V sériovém obvodu platí, že na všech součástkách je stejný proud. Pro paralelní zapojení platí, že na všech součástkách je stejné napětí. Proto je kreslení fázorových diagramů pro oba typy zapojení analogické, pouze si proud a napětí „prohodí role“.

• Rozbor úlohy

  Nejprve si nakreslíme fázorový diagram pro celý obvod. Při kreslení fázorového diagramu musíme zohlednit fázový posun mezi napětím a proudem elektromotorem, který je tvořen cívkou a rezistorem v sériovém zapojení.

  Z fázorového diagramu celého paralelního zapojení odvodíme vztah mezi proudy elektromotorem a kondenzátorem tak, aby platilo, že výsledný proud je ve fázi s napětím ze zdroje. V tomto vztahu vystupuje také fázové posunutí mezi napětím a proudem elektromotorem. Fázové posunutí napětí a proudu na elektromotoru si vyjádříme z jeho příkonu.

  Ze znalosti Ohmova zákona pro obvod se střídavým proudem vyjádříme kapacitanci paralelně připojeného kondenzátoru jako podíl zadaného napětí a vypočítaného proudu. Z kapacitance potom získáme kapacitu kondenzátoru.

• Řešení – fázorový diagram

  Jedná se o sériovo–paralelní zapojení, které budeme řešit postupně. Nejdříve vyřešíme sériové zapojení rezistoru a cívky (představují elektromotor). Pro toto zapojení můžeme nakreslit následující fázorový diagram:

  

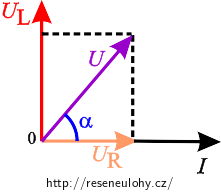
  Nyní nakreslíme fázorový diagram pro paralelní zapojení elektromotoru a kondenzátoru. V paralelním zapojení je na všech součástkách stejné napětí, proto v diagramu bude jeden, pro obě větve společný, fázor napětí a dva fázory proudu. Proud na kondenzátoru předbíhá napětí o π/2. I při zakreslování proudu I_RL, který protéká větví rezistor–cívka, musíme zohlednit fázový posun mezi napětím a proudem, který jsme určili pomocí předcházejícího fázorového diagramu.

  

  Výsledný proud má být ve fázi s napětím, fázorový diagram pro celkové zapojení tedy musí vypadat takto: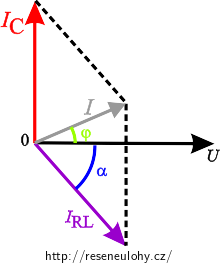

  

• Řešení

  Pro paralelní zapojení kondenzátoru a elektromotoru platí, že napětí na obou větvích jsou stejná:

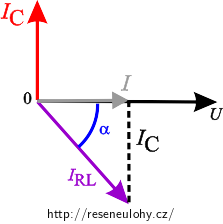
  \[U_\mathrm{C}=U_\mathrm{RL}=U.\]

  Výsledný proud má být ve fázi s napětím, fázorový diagram pro celkové zapojení tedy musí vypadat takto:

  

  Pozn.: Ve fázorovém diagramu je úhel α velikost fázového posunutí mezi napětím a proudem ze sériového zapojení rezistoru a cívky (představující elektromotor).

   

  Pomocí fázorového diagramu můžeme odvodit vztah mezi amplitudami proudu v obou větvích obvodu:

  \[I_\mathrm{C}=I_\mathrm{RL}\,\mathrm \sin \alpha.\]

  Kapacitanci kondenzátoru X_C si vyjádříme pomocí proudu I_C a napětí zdroje U:

  \[X_\mathrm{C}=\frac{U}{I_\mathrm{C}},\]

  dosadíme vztah mezi kapacitou C a kapacitancí X_C:

  \[\frac{1}{2\pi f C} = \frac{U}{I_\mathrm{C}}\]

  a vyjádříme kapacitu C:

  \[2\pi f C=\frac{I_\mathrm{C}}{U},\] \[C=\frac{I_\mathrm{C}}{2 \pi f U}.\]

  Dosadíme za proud I:

  \[C=\frac{I_\mathrm{RL}\,\mathrm \sin \alpha}{2 \pi f U}.\]

  Ze zadání víme, jaký má motor příkon P při připojení na napětí U s protékajícím proudem I_RL. Z toho můžeme odvodit, jakou hodnotu má fázový posun α mezi napětím a proudem na elektromotoru.

  Příkon motoru tedy vyjádříme jako:

  \[P=U I_\mathrm{RL} \mathrm \cos \alpha .\]

  Kosinus úhlu α (tzv. účiník) vyjádříme jako:

  \[ \mathrm{\cos \alpha}=\frac{P}{U I_\mathrm{RL}} .\]

  Z tohoto vyjádření získáme hodnotu fázového posunu mezi napětím a proudem α na elektromotoru a dosadíme ji do vyjádření pro kapacitu kondenzátoru.

• Zápis, výpočet, číselné dosazení

  U = 230 V	napětí zdroje
  f = 50 Hz	frekvence napětí zdroje
  P = 750 W	příkon elektromotoru při proudu IRL = 4 A
  α = ? (°)	velikost fázového posunutí mezi napětím a proudem
  C = ? (F)	kapacita kondenzátoru

  ---

  Vyjádříme si velikost úhlu α z následujícího vztahu:

  \[ \mathrm{\cos \alpha}=\frac{P}{U I_\mathrm{RL}}=\frac{750}{230 {\cdot} 4}\overset{\cdot}{=}0{,}8 \] \[ \alpha=35{,}4^{\circ} .\]

  Dosadíme velikost úhlu do vyjádření pro kapacitu kondenzátoru:

  \[C=\frac{I_\mathrm{RL}\, \mathrm{\sin \alpha}}{2 \pi f U}=\frac{4\, \mathrm{\sin \left(35{,}4^{\circ}\right)}}{2\pi \cdot 50 {\cdot} 230}\,\mathrm F=32{,}1\,\mathrm {\mu F}.\]

• Odpověď

  Kapacita paralelně připojeného kondenzátoru by měla mít hodnotu přibližně 32,1 μF, aby byl výsledný proud ve fázi s napětím.

• Komentář k elektromotoru

  V této úloze se pro jednoduchost řešení předpokládalo, že motor je složen ze sériového zapojení rezistoru a cívky a z paralelního připojení kondenzátoru. Obecně platí, že motor je součástka s impedancí a fázovým posunem mezi napětím a proudem. Pro řešení úlohy není třeba znát konkrétní zapojení jednotlivých součástek. V obecném případě bychom pro tuto úlohu vycházeli rovnou z fázorového diagramu pro paralelní zapojení.