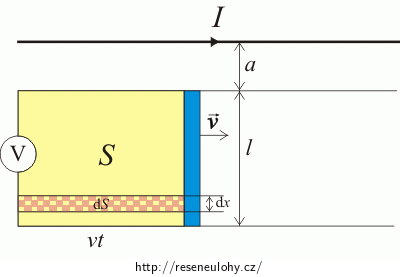
Pohybující se kovová tyč v blízkosti vodiče, jímž prochází proud
Úloha číslo: 801
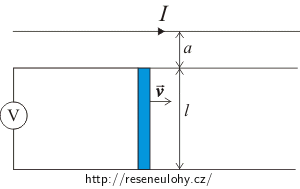
Kovová tyč o délce l = 1 m se pohybuje stálou rychlostív = 2 ms-1 rovnoběžně s dlouhým přímým drátem, jímž prochází proud I = 20 A. Vzdálenost mezi drátem a tyčí je a = 0,1 m. Spočítejte elektromotorické napětí indukované v tyči (kovová tyč je na obrázku znázorněna modře).
Nápověda 1
Jak definujeme indukované napětí?
Nápověda 2: Magnetický indukční tok
Magnetická indukce není v celé ploše smyčky konstantní. Jak budeme počítat magnetický indukční tok?
Řešení
Zajímá nás velikost indukovaného napětí, která je dána vztahem
\[U_\mathrm{i}=\left|-{\frac{\mathrm d\Phi}{\mathrm dt}}\right| ,\]což je změna magnetického toku dΦ za určitý časový úsek dt.
Magnetický indukční tok Φ spočítáme jako integrál magnetické indukce B
\[\Phi=\int{B}\,\mathrm dS.\]Velikost magnetické indukce B budeme počítat pomocí vzorce pro nekonečně dlouhý přímý vodič odvozeného v úloze Magnetické pole dlouhého přímého vodiče s proudem:
\[B= \frac{\mu_\mathrm{0}}{2\,\pi}\frac{I}{a+x}.\]Dosadíme do integrálu a element dS vyjádříme s pomocí obrázku. Plochu S si rozdělíme na proužky, jejichž tloušťka je dx, protože tímto rozdělením vystihneme, že v každém kousku tyče je jiná velikost magnetické indukce (ta se vzdáleností od vodiče klesá) a délka vt; to nám vyjadřuje pohyb tyče podél drátu. V proužku je velikost magnetické indukce B všude stejná.
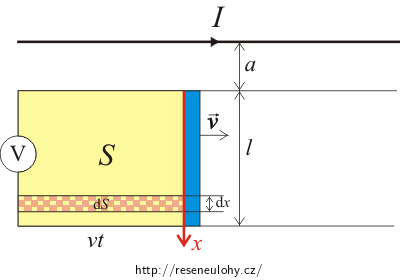
Integrujeme přes délku tyče. Pro magnetický indukční tok Φ dostáváme
\[\Phi=\int_0^\mathrm{l}{\frac{\mu_\mathrm{0}}{2\,\pi}\frac{I}{a+x}}\,vt\,\mathrm dx=\frac{\mu_0Ivt}{2\,\pi}\int_0^\mathrm{l}\frac{1}{a+x}\,\mathrm dx.\]Nyní substitucí vyřešíme integrál
substituce:\[y=a+x\] \[\mathrm dy=\mathrm dx\] \[\Phi=\frac{\mu_0Ivt}{2\,\pi}\int_\mathrm{a}^\mathrm{a+l}\frac{1}{y}\,\mathrm dy=\frac{\mu_0Ivt}{2\,\pi} \left[\ln{y}\right]_a^{a+l}=\frac{\mu_0Ivt}{2\,\pi} \left(\ln\left( {a+l}\right)-\ln a\right)=\frac{\mu_0Ivt}{2\,\pi} \cdot\ln {\frac {a+l}{a}}.\]Teď vše dosadíme do vztahu pro indukované napětí
\[U_\mathrm{i}=\left|-\frac{\mathrm d\Phi}{\mathrm dt}\right|=\left|-\frac{\mathrm d\frac{\mu_0Ivt}{2\,\pi}\cdot \ln {\frac{a+l}{a}}}{\mathrm dt}\right|=\left|-\frac{\mu_0Iv}{2\,\pi} \cdot \ln {\frac{a+l}{a}}\frac{\mathrm dt}{\mathrm dt}\right|=\left|-\frac{\mu_0 I v}{2\pi}\cdot\ln{\frac{a+l}{a}}\right|=\frac{\mu_0 I v}{2\pi}\cdot\ln{\frac{a+l}{a}}.\]Zápis a číselné dosazení
l = 1 m délka tyče v = 2 m·s-1 rychlost pohybu tyče I = 20 A proud procházející tyčí a = 0,1 m vzdálenost tyče od vodiče Ui = ? (V) indukované napětí Z tabulek: μ0 = 4π ·10-7 H·m-1 permeabilita vakua
\[U_\mathrm{i}=\frac{\mu_0 I v}{2\pi}\cdot\ln{\frac{a+l}{a}}=\frac{4\pi \cdot 10^{-7} \cdot 20{\cdot} 2}{2\pi}\cdot\ln{\frac{0{,}1+1}{0{,}1}}\,\mathrm V\,\dot{=}\,1{,}9{\cdot} 10^{-5}\,\mathrm V \,\dot{=}\, 19\,\mathrm {\mu V}\]Odpověď
V tyči se indukuje napětí 19 μV.
Odkaz na podobné úlohy