Jaké teplo vzniká v reálné cívce?
Úloha číslo: 164
K elektrické síti s amplitudou napětí 325 V a frekvencí 50 Hz je připojena cívka o indukčnosti 0,3 H a odporu 22 Ω. Jaké teplo předá cívka okolí za 30 sekund?
Zápis
Ze zadání známe:
Napětí zdroje: Um = 325 V Frekvence zdroje: f = 50 Hz Indukčnost cívky: L = 0,3 H Odpor cívky: R = 22 Ω Doba předávaní tepla: t = 30 s Chceme určit:
Teplo, které cívka předá okolí: Q = ? (J)Nápověda
Teplo, které má cívka předat okolí, nazýváme Jouleovým teplem a odpovídá energii elektrického proudu v této cívce.
Nápověda - Reálná cívka
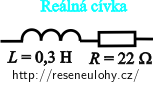
Reálná cívka má indukčnost i odpor. Schématicky reálnou cívku znázorňujeme jako cívku spojenou sériově s rezistorem.
Rozbor
V obvodu se střídavým proudem máme zařazenou reálnou cívku. Ta se vyznačuje tím, že je charakterizována jak indukčností, tak odporem. Teplo, které cívka předá do okolí během třiceti sekund, spočítáme jako Jouleovo teplo, které je rovno energii elektrického proudu v cívce za třicet sekund.
Řešení
Jouleovo teplo vypočítáme pomocí výkonu:
\[Q= P\,t.\]Jouleovo teplo, které cívka předá do okolí, budeme počítat pro střídavý proud. Vztah přepíšeme do tvaru:
\[Q= U_{\mathrm{ef}}\,I_{\mathrm{ef}}\,\left( \cos\varphi \right)\, t.\]Potřebujeme si vyjádřit efektivní hodnoty napětí a proudu.
Efektivní napětí vypočteme z amplitudy napětí, kterou známe ze zadání:
\[U_{\mathrm{ef}}=\frac{U_\mathrm{m}}{\sqrt 2}.\]Efektivní proud vypočteme z Ohmova zákona, kde celkovou impedanci tvoří kapacitance a rezistance:
\[I_{\mathrm{ef}}=\frac{U_{\mathrm{ef}}}{Z}=\frac{U_{\mathrm{ef}}}{\sqrt{R^2+\left(X_L\right)^2}}.\]Dosadíme-li do vzorce pro výpočet efektivní hodnoty proudu vztah pro efektivní napětí, získáme obecné vyjádření:
\[I_{\mathrm{ef}}=\frac{U_\mathrm{m}}{\sqrt {2\left(R^2+\left(X_L\right)^2\right)}}.\]Ještě si potřebujeme vyjádřit kosinus fázového posunutí mezi napětím a proudem. To uděláme pomocí fázorového diagramu.
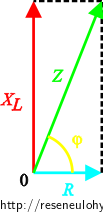
Kosinus fázového posunu vyjádříme jako:
\[\cos\varphi=\frac{R}{Z}=\frac{R}{\sqrt{R^2+\left(X_L\right)^2}}.\]Obecný vzorec pro vyjádření Jouleova tepla získáme ve tvaru:
\[Q=\frac{U_\mathrm{m}}{\sqrt 2}\, \frac{U_\mathrm{m}}{\sqrt {2\left(R^2+\left(X_L\right)^2\right)} }\,\frac{R}{\sqrt{R^2+\left(X_L\right)^2}}\,t=\frac{R\left(U_\mathrm{m}\right)^2}{2\,\left(R^2+\left(X_L\right)^2\right)}\,t=\frac{R\left(U_\mathrm{m}\right)^2}{2\,\left(R^2+\left(2\pi f L\right)^2\right)}\,t.\]
Číselný výpočet Jouleova tepla, které předá reálná cívka okolí během 30 sekund, je:
\[Q=\frac{22{\cdot} 325^2}{2\cdot \left(22^2+\left(2\pi\cdot 50 {\cdot} 0{,}3\right)^2\right)}\cdot 30\,\mathrm J\,\dot{=}\,3{,}7\,\mathrm kJ.\]Odpověď
Reálná cívka v obvodu se střídavým napětím o daných vlastnostech předá okolí za 30 sekund teplo přibližně 3,7 kJ.


