Časový průběh proudu cívkou
Úloha číslo: 722
V obvodu na obrázku je udržován konstantní celkový proud I změnami napětí zdroje. Spínač S je sepnut v čase t = 0 s. Odvoďte, jak závisí proud protékající cívkou na čase, který uplynul od sepnutí spínače, a určete, kdy je proud rezistorem stejný jako proud cívkou.
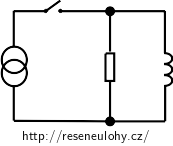
Nápověda
Po sepnutí spínače teče proud v obvodu nejprve převážně rezistorem, protože v cívce se indukuje napětí, které brání změně proudu, tj. tomu, aby cívkou najednou začal téci relativně velký proud. Postupně se bude proud cívkou zvětšovat, a tedy proud rezistorem zmenšovat. Poté, co se dosáhne ustáleného stavu, bude proud protékat pouze cívkou, protože má v porovnání s rezistorem zanedbatelný odpor (ideální cívka má dokonce nulový odpor).
Rozbor
Po sepnutí spínače platí, že celkový proud (který je zdrojem udržován na konstantní hodnotě) je roven součtu proudu rezistorem a cívkou. Dále platí, že indukované napětí na cívce bude v každém okamžiku stejné jako úbytek napětí na rezistoru. Z těchto poznatků sestavíme diferenciální rovnici pro průběh proudu a vyřešíme ji.
Řešení – odvození závislosti proudu na čase
Po sepnutí spínače se začne proud tekoucí cívkou zvětšovat, což způsobí, že se v ní bude indukovat napětí působící proti tomuto růstu. Podle 2. Kirchhoffova zákona bude indukované napětí v cívce v každém okamžiku stejné jako úbytek napětí na rezistoru.
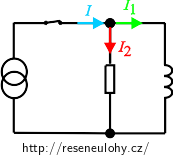
Označíme-li si proudy tekoucí cívkou a rezistorem podle obrázku, můžeme psát:
\[ U_\mathrm{L}=U_\mathrm{R}, \] \[ L \frac{\mathrm{d}I_1}{\mathrm{d}t}=RI_2. \]Z 1. Kirchhoffova zákona platí:
\[ I_1 + I_2 = I, \]což nám při konstantnosti proudu I umožňuje jednoduchými úpravami dospět k diferenciální rovnici pro závislost proudu I1 tekoucího cívkou na čase:
\[ L \frac{\mathrm{d}I_1}{\mathrm{d}t}=RI_2, \] \[ L \frac{\mathrm{d}I_1}{\mathrm{d}t}=R(I - I_1), \] \[ L \frac{\mathrm{d}I_1}{\mathrm{d}t} + RI_1 =RI. \]Získali jsme lineární diferenciální rovnici 1. řádu s pravou stranou. Její řešení uvedeme v následujícím oddíle.
Řešení – lineární diferenciální rovnice pro proud I1
\[ L \frac{\mathrm{d}I_1(t)}{\mathrm{d}t} + RI_1(t) =RI \]Obecné řešení rovnice tohoto typu můžeme vyjádřit jako součet obecného řešení příslušné diferenciální rovnice bez pravé strany (tzv. homogenní rovnice) a partikulárního řešení.
Poznámka: Tuto diferenciální rovnici lze řešit také jednodušeji metodou separace proměnných.
1.) Obecné řešení homogenní diferenciální rovnice:
Řešíme tedy rovnici ve tvaru:
\[ L \frac{\mathrm{d}I_1(t)}{\mathrm{d}t} + RI_1(t) = 0, \] \[\frac{\mathrm{d}I_1(t)}{\mathrm{d}t} + \frac{R}{L}I_1(t) = 0, \]kterou lze řešit např. pomocí metody separace proměnných:
\[\frac{\mathrm{d}I_1(t)}{\mathrm{d}t} = - \frac{R}{L}I_1(t) , \] \[\frac{1}{I_1(t)}\mathrm{d}I_1 = - \frac{R}{L}\mathrm{d}t , \] \[\int \frac{1}{I_1(t)}\mathrm{d}I_1 = \int (- \frac{R}{L})\mathrm{d}t , \] \[\ln |I_1(t)| = - \frac{R}{L}t + k , \]kde k je integrační konstanta. Po odlogaritmování a označení C = ek má řešení homogenní rovnice tvar:
\[I_1(t) = C{e}^\mathrm{- \frac{R}{L}t}. \]2.) Partikulární řešení diferenciální rovnice:
K nalezení partikulárního řešení použijeme metodu variace konstanty: Její princip spočívá v předpokladu, že řešení homogenní rovnice bude vyhovovat rovnici úplné, jestliže nahradíme konstantu C vhodnou funkcí. Budeme tedy předpokládat, že:
\[I_1(t) = C(t)e^\mathrm{- \frac{R}{L}t} \]je hledaným řešením a dosadíme tuto funkci do úplné rovnice.
Nejdříve si připravíme derivaci této funkce podle času (budeme značit čárkou) jako derivaci součinu:
\[I_1(t) = C(t) e^\mathrm{- \frac{R}{L}t}, \] \[I_1^,(t) = C^,(t) e^\mathrm{- \frac{R}{L}t} - \frac{R C(t)}{L}(t)e^\mathrm{- \frac{R}{L}t}.\]Nyní dosadíme tuto funkci a její výše připravenou derivaci do úplné rovnice a vyjádříme neznámou funkci C(t):
\[ L \frac{\mathrm{d}I_1(t)}{\mathrm{d}t} + RI_1(t) = RI ,\] \[ L ( C^,(t) e^\mathrm{- \frac{R}{L}t} - \frac{R C(t)}{L}(t)e^\mathrm{- \frac{R}{L}t}) + R C(t) e^\mathrm{- \frac{R}{L}t}= RI ,\] \[ L C^,(t) e^\mathrm{- \frac{R}{L}t} - R C(t) e^\mathrm{- \frac{R}{L}t} + R C(t) e^\mathrm{- \frac{R}{L}t}= RI ,\] \[ L C^,(t) e^\mathrm{- \frac{R}{L}t} = RI ,\] \[ C^,(t) = \frac{RI}{L} e^\mathrm{ \frac{R}{L}t}.\]Zintegrujeme podle času:
\[ C(t) = \frac{RI}{L} e^\mathrm{ \frac{R}{L}t} \frac{L}{R} + K,\] \[ C(t) = I e^\mathrm{ \frac{R}{L}t} + K,\]kde K je integrační konstanta.
3.) Úplné řešení diferenciální rovnice:
Vztah pro funkci C(t) dosadíme do výrazu pro řešení homogenní rovnice a získáme tak obecné řešení úplné rovnice:
\[I_1(t) = C(t) e^\mathrm{- \frac{R}{L}t}, \] \[I_1(t) = (I e^\mathrm{ \frac{R}{L}t} + K )e^\mathrm{- \frac{R}{L}t} \]a po úpravě:
\[I_1(t) = I + K e^\mathrm{- \frac{R}{L}t}. \]Konstantu K určíme z počátečních podmínek. Na počátku t = 0 s je proud tekoucí cívkou nulový, I0 = 0 A. Díky tomu dostáváme:
\[I_0 = I + K, \] \[0 = I + K, \] \[ K = -I. \]Závislost proudu tekoucího cívkou na čase pak můžeme zapsat ve tvaru:
\[I_1(t) = I -I e^\mathrm{- \frac{R}{L}t} = I ( 1 - e^\mathrm{- \frac{R}{L}t}). \]Řešení – rovnost proudu rezistorem a cívkou
Protože z 1. Kirchhoffova zákona platí:
\[ I_1 + I_2 = I, \]je zřejmé, že stejný proud cívkou a rezistorem poteče v okamžiku, kdy bude platit:
\[ I_1 = \frac{I}{2}.\]Po dosazení do výrazu odvozeného v oddílu výše získáváme:
\[I_1(t) = I ( 1 - e^\mathrm{- \frac{R}{L}t}), \] \[\frac{I}{2} = I ( 1 - e^\mathrm{- \frac{R}{L}t}), \] \[\frac{1}{2} = 1 - e^\mathrm{- \frac{R}{L}t}, \] \[ e^\mathrm{- \frac{R}{L}t}= \frac{1}{2} . \]Zlogaritmujeme:
\[ - \frac{R}{L}t= \mathrm{ln}\frac{1}{2} , \] \[ \frac{R}{L}t= -\mathrm{ln}2 . \]Vyjádříme čas t:
\[ t= -\frac{L}{R}\,\mathrm{ln}2 . \]Odpověď
Závislost proudu protékajícího cívkou na čase popisuje rovnice:
\[I_1(t) = I ( 1 - e^\mathrm{- \frac{R}{L}t}). \]Stejně velký proud poteče rezistorem a cívkou v čase:
\[ t= -\frac{L}{R}\,\mathrm{ln}2 . \]


