Sbírka řešených úloh

Dvě navzájem kolmé nabité přímky

Úloha číslo: 1020

• Nápověda 1

  Nakreslete si obrázek situace a zvolte si souřadnicový systém.

• Řešení nápovědy

  Na nabitých přímkách zvolíme osy x a y.

  

  Na uvedené siločáře procházející počátkem si vyznačíme bod A o souřadnicích x a y.

• Nápověda 2

  Uvědomte si, že intenzita výsledného pole musí mít směr siločáry. Co z toho plyne pro směr intenzity v bodě A, který leží na siločáře procházející průsečíkem přímek?

• Řešení nápovědy

  Intenzita v bodě A musí ležet na přímce, která prochází počátkem.

  Podrobnější informace o elektrické intenzitě v okolí nabité přímky naleznete v úloze Pole nabité přímky. Tady si jen uvedeme vzorec pro výpočet velikosti elektrické intenzity E: \[E=\frac{\lambda}{2\pi \epsilon_0 z},\] kde λ je hustota náboje, z vzdálenost, ve které počítáme velikost elektrické intenzity E a ε₀ je permitivita vakua, která je velmi blízká permitivitě vzduchu, a proto ji zde použijeme.

  Je-li přímka nabitá kladně, směřuje vektor intenzity od ní, je-li nabitá záporně, vektor intenzity směřuje k ní.

• Celková intenzita v bodě A

  Celkovou intenzitu \(\vec{E}_\mathrm A\) v bodě A spočítáme jako vektorový součet intenzit od obou přímek, tj. \(\vec{E}_1\) od přímky s lineární hustotou náboje τ₁ a \(\vec{E}_2\) od přímky s lineární hustotou náboje τ₂: \[\vec{E}_\mathrm A=\vec{E}_1+\vec{E}_2.\]

• Jak je to s intenzitou v ostatních bodech?

  K lepšímu pochopení úlohy je vhodné nakreslit si celkové intenzity nejenom v bodě A, ale i v bodech B a C, které jsou rozmístěny, jak je vidět na obrázku.

  

  Obě přímky považujte za kladně nabité, to jednoznačně určuje směr elektrické intenzity.

  

  Je-li přímka nabitá kladně, elektrická intenzita směřuje od přímky.

  Všechny tři body jsou ve stejné vzdálenosti od svislé přímky, tj. vodorovná složka intenzity bude stejná pro všechny tři, ale svislá složka se bude zmenšovat s rostoucí vzdáleností od vodorovné přímky. Proto jen v jednom bodě přímky, na které leží body A, B a C, nastane ten případ, že \(\vec{E}\) má stejný směr jako spojnice s počátkem.

• Rozbor

  Pro vyřešení této úlohy je nutné si uvědomit, že intenzita výsledného pole musí mít směr siločáry. Z toho plyne, že v bodech na uvedené přímkové siločáře platí, že úhel, který svírá siločára s vodorovnou přímkou, je stejný jako úhel, který svírá výsledná intenzita s vodorovným směrem.

• Řešení

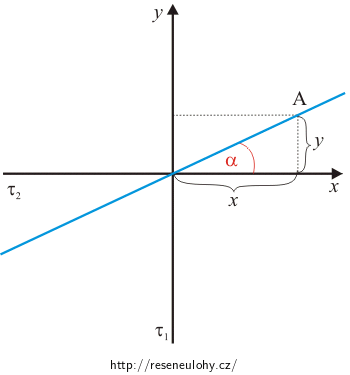
  Máme určit úhel α, který svírá siločára popsaná v zadání s přímkou o lineární hustotě τ₂. Na siločáře si zvolíme bod A o souřadnicích x a y. Pro úhel α platí

  \[\mathrm{tg}\,\alpha=\frac{y}{x},\]

  jak je vidět na obrázku. Nabité přímky leží na osách a siločára je vyznačena modře.

  

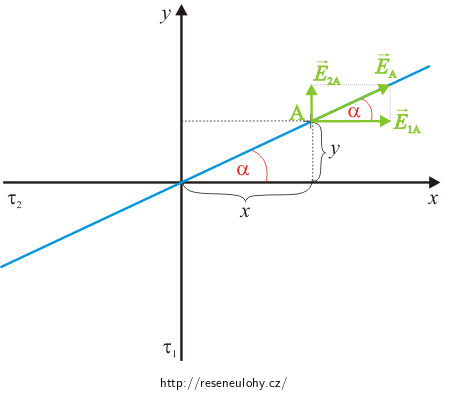
  Pozn.: V obrázku uvažujeme přímky s kladným nábojem.

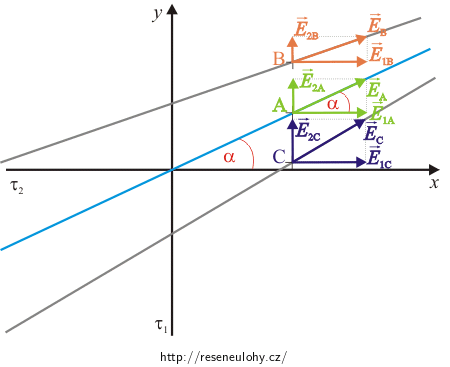
  Vektor celkové intenzity \(\vec{E}\) musí mít vždy směr siločáry, tj. v bodě A bude mít směr přímky procházející počátkem. To znamená, že úhel, který svírá vektor \(\vec{E}_\mathrm A\) s vodorovným směrem, je stejný jako úhel α, který máme určit. S využitím vzorce pro velikost elektrické intenzity v okolí nabité přímky \(E=\frac{\lambda}{2\pi \epsilon_0 z}\) můžeme psát

  \[ \mathrm{tg}\,\alpha=\frac{E_{2\mathrm A}}{E_{1\mathrm A}}=\frac{\frac{\tau_2}{2\pi\epsilon_0y}}{\frac{\tau_1}{2\pi\epsilon_0x}}=\frac{\tau_2x}{\tau_1y}, \]

  kde E_1A je velikost elektrické intenzity jedné nabité přímky a E_2A je velikost elektrické intenzity druhé nabité přímky.

  Z toho plyne:

  \[\frac{y}{x}=\frac{\tau_2x}{\tau_1y}.\]

  Neznámý poměr \(\frac{y}{x}\) si převedeme na stejnou stranu:

  \[\frac{y^2}{x^2}=\frac{\tau_2}{\tau_1}\qquad \Rightarrow \qquad {\mathrm{tg}\,^2\alpha}=\frac{\tau_2}{\tau_1}.\]

  Odtud již vyjádříme úhel α:

  \[ \mathrm{tg}\,\alpha=\sqrt{\frac{\tau_2}{\tau_1}}, \] \[ \alpha=\mathrm{arctg}\,\sqrt{\frac{\tau_2}{\tau_1}}. \]

  Pozn. v případě, že by \(\tau_1\) a \(\tau_2\) byly záporné, orientace vektorů elektrické indkuce by byla opačná. Ve výpočetu by se nic nezměnilo.

• Odpověď

  Siločára svírá s přímkou nabitou nábojovou hustotou τ₂ úhel \[ \alpha=\mathrm{arctg}\,\sqrt{\frac{\tau_2}{\tau_1}}. \]

• Dynamický prvek

  Následující aplet zobrazuje dvě kolmé nabité přímky (červenou a oranžovou) a bod (znázorněný zeleně) umístěný mezi nimi. Bodem lze posouvat pomocí myši a pomocí pousuvníků lze nastavit délkovou hustotu náboje na každé z přímek. Aplet zobrazuje elektrickou intenzitu v bodě A od každé z přímek a také výslednou elektrickou intenzitou od obou přímek.

   

  Úkoly pro práci s apletem

  1. Nastavte bod A do různých míst a sledujte směr výslené intenzity.
  2. Najděte polohu bodu A tak, aby výslednice elektrické intenzity splývala s černou přímkou (měla směr této přímky). Posouvejte bod A po této přímce a pozorujte změny velikosti \({E_1},\space {E_2},\space E_V.\)
  3. Postupných zkoušením najděte hodnoty lineárních hustot nábojů tak, aby siločára procházející počátkem svírala s vodorovnou přímkou úhel \(30°,\space 45°, \mathrm{resp.}\space 60°.\) Ověřte výsledný vztah získaný v řešení úlohy.