Dutý válcový vodič
Úloha číslo: 54
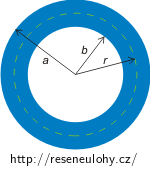
Na obrázku je průřez dutého válcového vodiče, jehož vnější poloměr je a a vnitřní poloměr b. Vodičem protéká proud I homogenně rozložený v celém průřezu vodiče.
a) Dokažte, že závislost velikosti magnetické indukce na vzdálenosti od středu vodiče má tvar
\[B=\frac{\mu_0 I}{2\pi(a^{2}-b^{2})}\,\frac{r^{2}-b^{2}}{r}\]pro a ≥ r ≥ b.
b) Dokažte, že
1) pro r = a dává tato rovnice velikost magnetické indukce stejnou jako vně dlouhého přímého vodiče,
2) pro r = b bude výsledná magnetická indukce rovna nule,
3) pro b = 0 dostaneme vztah pro magnetickou indukci uvnitř plného vodiče.
Nápověda
Protože se jedná o homogenní rozložení proudu, bude vytvořené magnetické pole válcově symetrické. Pro určení magnetického pole použijeme Ampérův zákon.
Nápověda - Ampérův zákon
Ampérův zákon
Celkový proud procházející plochou, kterou ohraničuje uzavřená křivka, vynásobený permeabilitou vakua se rovná integrálu magnetické indukce podél této křivky:
\[\mu_\mathrm{0} I_\mathrm{c} = \oint_\Gamma{\vec{B}}\cdot\vec{\mathrm{d}l}.\]Rozbor
Příklad budeme řešit pomocí Ampérova zákona (viz Nápověda 2). Křivkou bude kružnice o poloměru r. Díky symetrii úlohy se křivkový integrál velmi zjednoduší. Proud procházející plochou zvolené křivky určíme z konstantní hustoty proudu v celém průřezu vodiče.
Řešení a)
Jak již bylo zmíněno v rozboru, úlohu budeme řešit pomocí Ampérova zákona
\[\oint{\vec{B}}\cdot \mathrm{d}\vec{s}=\mu_\mathrm{0}I_\mathrm{c}.\]Ampérovou křivkou bude kružnice. Díky symetrii úlohy je směr vektoru magnetické indukce \(\vec{B}\) tečný k této křivce, má tedy stejný směr jako \(d\vec{s}\). Ampérův zákon můžeme proto psát ve tvaru
\[\oint{B}\,\mathrm{d}s=\mu_\mathrm{0}I_\mathrm{c}.\]Ze symetrie dále vyplývá, že velikost magnetické indukce B podél celé kružnice je konstantní a stačí tedy vynásobit velikost magnetické indukce B délkou křivky. Levou stranu Ampérova zákona můžeme tedy vyjádřit jako
\[\oint{B}{\mathrm{d}s}=B2\pi r.\]Proud Ic procházející plochou vyjádříme pomocí hustoty proudu J
\[J=\frac{I_\mathrm{c}}{S_\mathrm{c}}=\frac{I}{S},\]kde Ic je proud, který protéká uvnitř zvolené kružnice o poloměru r,
Sc je obsah části vodiče s proudem, který je ohraničený kružnicemi o poloměrech b a r,
I je proud protékající celou plochou vodiče,
S je obsah průřezu celého vodiče s proudem, který je ohraničen kružnicemi o poloměrech a a b.
Obsahy vodiče s proudem Sc a S (viz obrázek) můžeme vyjádřit jako
\[S=\pi a^{2} - \pi b^{2}=\pi \left(a^{2} - b^{2}\right)\] \[S_c=\pi r^{2} - \pi b^{2}=\pi \left(r^{2} - b^{2}\right).\]Po dosazení obsahů do rovnice pro hustotu dostáváme
\[\frac{I_\mathrm{c}}{\pi \left(r^{2} - b^{2}\right)}=\frac{I}{\pi \left(a^{2} - b^{2}\right)}.\]Odtud vyjádříme proud Ic
\[I_\mathrm{c}=\frac{r^{2} - b^{2}}{ a^{2} - b^{2}}I\]a ten dosadíme do pravé strany Ampérova zákona:
\[\mu_0 I_\mathrm{c} =\mu_0 I \frac{ r^{2} - b^{2}}{a^{2} - b^{2}}.\]Nyní již máme vyjádřeny obě strany Ampérova zákona:
\[B2\pi r = \mu_0 I \frac{ r^{2} - b^{2}}{ a^{2} - b^{2}}.\]Odtud vyjádříme hledanou magnetickou indukci B:
\[B=\frac{\mu_0 I}{2\pi\left(a^{2}-b^{2}\right)}\frac{r^{2}-b^{2}}{r}.\]Dokázali jsme tak, že pro závislost magnetické indukce na vzdálenosti od středu vodiče platí uvedený vztah.
Řešení b)
1.) Do vyjádření velikosti magnetické indukce odvozené v části a)
\[B=\frac{I}{2\pi(a^{2}-b^{2})}\,\frac{r^{2}-b^{2}}{r}\tag{*}\]dosadíme r = a:
\[B=\frac{I}{2\pi(a^{2}-b^{2})}\,\frac{a^{2}-b^{2}}{a}.\]Po úpravě dostáváme vztah
\[B=\frac{\mu_0 I}{2\pi a},\]který odpovídá magnetické indukci vně dlouhého přímého vodiče.
2.) Dále do (*) dosadíme r = b:
\[B=\frac{I}{2\pi(a^{2}-b^{2})}\,\frac{b^{2}-b^{2}}{b}\] \[B=0.\]3.) Pro hodnotu b = 0, dostáváme
\[B=\frac{I}{2\pi a^{2}}\,\frac{r^{2}}{r}\]\[B=\frac{\mu_0 I}{2\pi a^2}\,r.\]Jedná se o vzorec pro magnetickou indukci uvnitř dlouhého přímého vodiče.


