Magnetické pole v okolí dvou nekonečně dlouhých vodičů
Úloha číslo: 2304
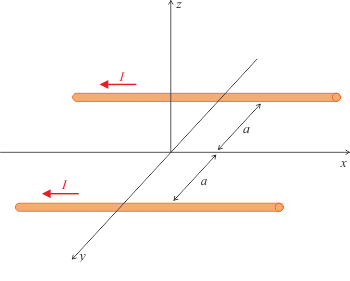
Uvažujme dva nekonečně dlouhé vodiče, vzdálenost mezi nimi je \(2a\). Oběma protéká proud \(I\) v záporném směru osy x. Zakreslete tvar magnetického pole v rovině yz. Nalezněte bod na ose z, kde je magnetické pole maximální. Volba souřadnicového systému je vyznačena na obrázku.
Nápověda – magnetické pole v okolí vodiče
Uvažujme bod ve vzdálenosti \(R\) od přímého vodiče s proudem \(I\). Jaká je velikost magnetické indukce v tomto bodě? Jaký je směr magnetické indukce?
Nápověda pro zakreslení tvaru magnetického pole
Výsledný tvar magnetického pole v okolí vodičů vznikne sečtením příspěvků od obou vodičů. Uvědomme si, že velikost magnetického pole klesá se vzdáleností, tedy pokud jsme blízko jednoho vodiče, bude vliv druhého vodiče v porovnání s příspěvkem prvního vodiče minimální.
Řešení zakreslení tvaru magnetického pole
Zaměřme se na magnetické pole v blízkém okolí levého vodiče. Magnetické indukční čáry jsou téměř kružnice (magnetické pole je ovlivňováno polem od pravého vodiče, ale jelikož velikost magnetického pole klesá se vzdáleností, tak toto ovlivnění není velké). Stejně tak magnetické indukční čáry v blízkém okolí pravého vodiče jsou téměř kružnice.
Magnetické pole v počátku soustavy souřadnic bude nulové, jelikož se příspěvky vzájemně odečtou.
Zakresleme si příspěvky od každého z vodičů v bodě na ose z.
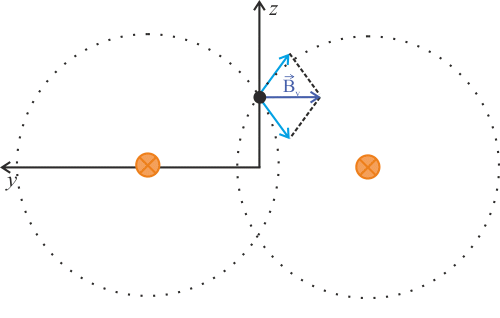
Z obrázku je zřejmé, že magnetická indukce na ose z je kolmá na osu z a rovnoběžná s osou y.
Analogicky zakreslíme příspěvky a jejich výslednice v dalších místech, čímž si uděláme představu o tvaru magnetického pole v okolí vodičů.
Náčrt tvaru magnetického pole pomocí magnetických indukčních čarTvar magnetického pole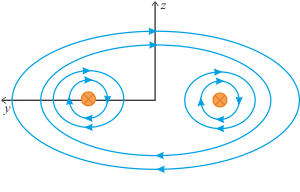
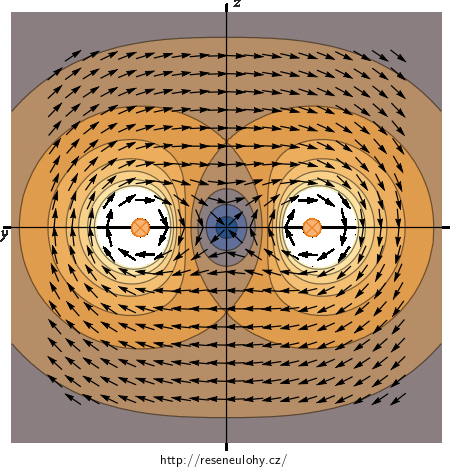
Popis obrázku: Barva ukazuje velikost magnetického pole v daném místě. Světlá barva odpovídá velkým hodnotám a tmavá barva malým hodnotám. Šipky jsou všude stejně dlouhé a znázorňují pouze směr magnetického pole v daném místě. Šipky nejsou nakresleny těsně u vodičů z důvodu přehlednosti obrázku.
Řešení – průběh magnetického pole podél osy z
Jelikož chceme najít takový bod na ose z, ve kterém má magnetické pole na ose největší velikost, odvodíme vztah, jenž bude popisovat velikost magnetického pole pro každý bod na ose z, a poté najdeme jeho maximum.
Zvolme bod P na ose z o souřadnicích \(P=[0;0;z]\) a zakresleme příspěvky magnetické indukce od obou vodičů.
Protože víme, že magnetické pole kolem nekonečného vodiče s proudem má tvar soustředných kružnic, můžeme hned psát, že složka kolmá k rovině yz (tj. k obrázku) je nulová:
\[B_\mathrm{x}=0 \space \mathrm{T},\]jelikož vektor magnetické indukce příspěvků od obou vodičů leží v rovině yz.
Bod P je stejně vzdálen od obou vodičů, takže příspěvky k \(\vec{B}\) od obou vodičů jsou stejně velké.
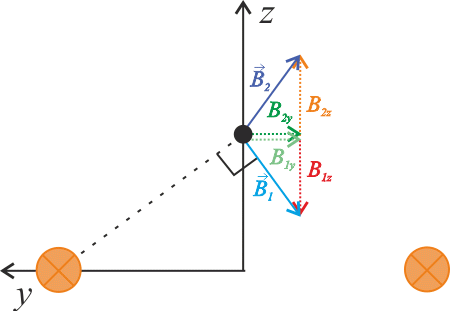
Z obrázku je patrné, že z složka magnetické indukce od prvního vodiče \(B_\mathrm{1z}\) má stejnou velikost a opačný směr než z složka magnetické indukce od druhého vodiče \(B_\mathrm{2z}\). Tudíž výsledné pole bude mít z složku rovnu nule. Toto platí pro každý bod na ose z. Můžeme tedy napsat, že pro každý bod P o souřadnicích \(P=[0;0;z]\) platí
\[B_\mathrm{z}=0\space \mathrm{T}.\]Nenulová tedy bude jen y složka celkové magnetické indukce. Z obrázku dále můžeme vidět, že y složka magnetické indukce od prvního vodiče \(B_\mathrm{1y}\) má stejnou velikost i směr jako y složka magnetické indukce od druhého vodiče \(B_\mathrm{2y}\). Tedy můžeme psát
\[B_\mathrm{y}=B_\mathrm{1y}+B_\mathrm{2y}=2B_\mathrm{1y},\tag{1}\]kde \(B_\mathrm{1y}\) je y složka příspěvku od prvního vodiče a \(B_\mathrm{2y}\) je y složka příspěvku od druhého vodiče. Toto platí opět pro každý bod na ose z.
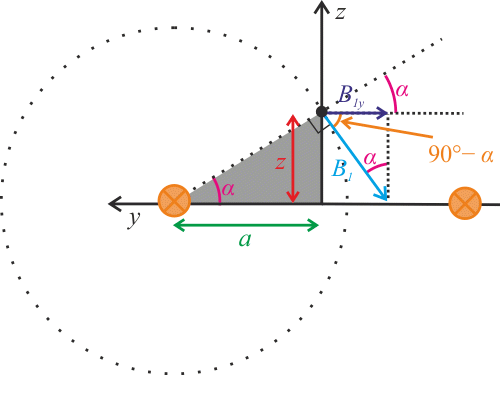
Nyní pro každý bod P o souřadnicích \(P=[0;0;z]\) vyjádříme y složku magnetické indukce od prvního vodiče:
\[B_\mathrm{1y}=B_{1}\sin\alpha,\]kde \(B_{1}\) je velikost magnetického pole od prvního vodiče, kterou vyjádříme pomocí vzorce (viz nápověda)
\[B_{1}=\frac{\mu_0}{2\pi}\frac{I}{R}=\frac{\mu_0 }{2\pi}\frac{I}{\sqrt{a^2+z^2}}.\]\(\sin\alpha\) vyjádříme z šedého pravoúhlého trojúhelníku podle definice
\[\sin\alpha=\frac{z}{\sqrt{a^2+z^2}}.\]Spojením posledních tří vztahů získáme
\[B_\mathrm{1y}=\frac{\mu_0 }{2\pi}\frac{I}{\sqrt{a^2+z^2}}\frac{z}{\sqrt{a^2+z^2}}=\frac{\mu_0 }{2\pi}\frac{Iz}{{a^2+z^2}}.\]Dosazením posledního výrazu do vztahu (1) získáme
\[B_\mathrm{y}=2B_\mathrm{1y}=\frac{\mu_0 }{\pi}\frac{Iz}{{a^2+z^2}}.\tag{2}\]Odvodili jsme, že pro každý bod o souřadnicích \([0;0;z]\) platí
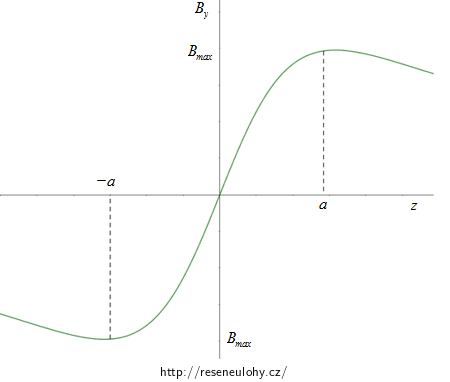
\[\vec{B}=\left(0,\frac{\mu_0 }{\pi}\frac{Iz}{{a^2+z^2}},0\right).\]Graf složky y magnetické indukce na souřadnici z v bodech na ose z ukazuje následující obrázek. Velikost magnetické indukce odpovídá velikosti této složky.
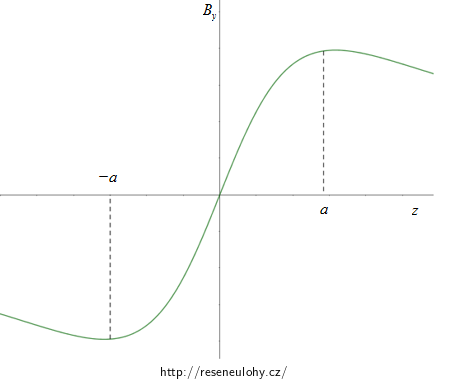
Všimněte si, že graf odpovídá našemu pozorování. Pro \(z=0\) je magnetické pole nulové, protože se příspěvky navzájem odečetly (příspěvky od jednotlivých vodičů mají nenulovou jen složku z). S rostoucím z magnetické pole nejdříve roste a poté zase klesá k nule (ve velké vzdálenosti). Záporné hodnoty y složky magnetické indukce znamenají, že B míří opačným směrem.
Řešení – místo s největším magnetickým polem na ose z
Naším úkolem je najít bod, ve kterém je velikost magnetické indukce maximální, tedy hledáme maximum \(B_\mathrm{y}\)
\[B_\mathrm{y}=\frac{\mu_0 }{\pi}\frac{Iz}{{a^2+z^2}}.\]Pozn.: Následující výpočet využívá poznatků diferenciálního počtu. Pokud s touto matematikou nemáte zkušenosti, hledejte látku pod klíčovým slovem vyšetřování průběhu funkce.
Pro nalezení maxima využijeme poznatků z matematiky, tedy skutečnosti, že v maximu je derivace funkce nulová
\[\frac{\mathrm{d}B_\mathrm{y}}{\mathrm{d}z}=0.\]Vztah pro \(B_\mathrm{y}\) derivujme podle z, využijeme pravidlo pro derivaci podílu
\[\frac{\mu_0 I}{\pi}\frac{a^2+z^2-z\,(0+2z)}{(a^2+z^2)^2}=0,\] \[\frac{\mu_0 I}{\pi}\frac{a^2-z^2}{(a^2+z^2)^2}=0.\]Rovnost je splněna pro
\[z=\pm \space a.\]Z důvodu symetrie se omezíme pouze na z=a, druhé místo se stejně velkým magnetickým polem je pro \(z=-a\) a míří opačným směrem. Velikost maximální magnetické indukce dopočítáme dosazením do výrazu (2).
\[B_\mathrm{{y,max}}=\frac{\mu_0 }{2\pi}\frac{I}{{a}}.\] KomentářMaximální magnetické pole na ose z je v bodech \(\pm a\) a má velikost \(B_\mathrm{max}=\frac{\mu_0 }{2\pi}\frac{I}{{a}}\) a směr ve směru osy y. V bodech \(\pm a\) bychom získali pole o stejné velikosti, pokud bychom namísto dvou vodičů umístili jeden vodič s proudem \(I\) do počátku soustavy souřadnic. Pokud by proud tekl také do obrazovky, pak by magnetické pole mělo v těchto dvou bodech i stejný směr. V jiných bodech osy z by ale mělo magnetické pole jinou hodnotu!
Odpověď
Tvar magnetického pole v rovině yz naznačuje následující obrázek

Velikost magnetické indukce je na ose z maximální v bodech \(z=a\) a \(z=-a\), velikost magnetické indukce je zde \(B_\mathrm{max}=\frac{\mu_0}{2\pi}\frac{I}{a}.\)
Následující graf zobrazuje závislost složky y magnetické indukce na souřadnici z. V grafu jsou zobrazeny body \(z=\pm a\), pro něž platí, že velikost magnetického pole je zde největší.