Homogenně polarizovaný válec
Úloha číslo: 239
Velmi dlouhý válec o poloměru a je homogenně polarizován; vektor polarizace \(\vec{P}\) je kolmý na osu válce. Najděte průběh elektrického pole uvnitř i vně válce.
Dejte pozor! Polarizace je homogenní, nikoliv radiální! Vektor polarizace má ve všech místech válce stejný směr a velikost.
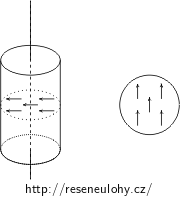
Homogenně polarizovaný válec. Vektor polarizace v jeho průřezu.
Rozbor
Příklad lze řešit drobným trikem: ideální dipóly ve válci si představíme jako neideální, kladné a záporné náboje ve velmi malé vzájemné vzdálenosti d. Protože polarizace je homogenní, jsou všechny dipóly stejně orientovány. Když z těchto neideálních dipólů vezmeme jenom kladný náboj, utvoří kladně nabitý válec; obdobně záporné náboje utvoří záporně nabitý válec. Tyto válce jsou oproti sobě maličko posunuté.
Výsledné pole pak dostaneme superpozicí polí obou rovnoměrně nabitých válců, které umíme spočítat (například pomocí Gaussovy věty). Výsledek bude závislý na velikosti uvažovaného posunutí d obou válců. Protože toto posunutí považujeme za velmi malé, můžeme provést aproximaci do prvního řádu ve členu d a protože pro dipólový moment platí p = qd a polarizace je vlastně „objemová hustota dipólů“ (přesněji hustota dipólového momentu), platí
\[\vec P = \frac{1}{V}\vec p = \frac{q}{V}\vec d = \varrho\vec d.\]Pomocí tohoto vztahu můžeme po aproximaci do prvního řádu vyjádřit uvažované „neznámé posunutí“ d pomocí vektoru polarizace, který je zadán.
Pole nabitého válce
Pole válce s rovnoměrně rozloženým objemovým nábojem je vyšetřováno v úloze Pole nabitého válce.
Nápověda 1
Představte si válec jako dva válce vyplněné rovnoměrně kladným a záporným nábojem (při úplném překryvu se vyruší, což odpovídá elektricky neutrálním atomům či molekulám).
Polarizace odpovídá „malému posunutí kladného a záporného válce vůči sobě“. Jejich osy se od sebe vzdálí o nepatrnou vzdálenost d, přičemž ale můžeme předpokládat, že posunutí je tak nepatrné, že se jinak rozložení náboje nedotkne.
Nápověda 2
Použijte také fakt ihned plynoucí z Gaussovy věty: uvnitř i vně velmi dlouhého válce s konstantní hustotou objemového náboje ρ má intenzita elektrického pole ve válcových souřadnicích pouze radiální složku, která má ve vzdálenosti s od osy uvnitř válce velikost
\[E = \frac{\varrho}{2\varepsilon_0}s\]a vně válce má velikost
\[E = \frac{\varrho a^2}{2\varepsilon_0}\frac{1}{s}.\]Detailní postup lze najít v úloze Pole nabitého válce.
Výsledné pole pak dostanete pomocí superpozice polí kladného a záporného válce. To bude závislé na posunutí d. Protože posunutí je nepatrné, můžete provést aproximaci prvního řádu vůči d. Pak si jen uvědomte, jak souvisí dipólový moment s posunutím a s vektorem polarizace.
Nápověda 3
Pro pole uvnitř válce použijte vztah v předchozí nápovědě a princip superpozice polí válce kladného a záporného. Uvědomte si, že rozdíl vektorů spojujících osy obou válců s místem, kde pole zkoumáme, je roven vektoru \(\vec{d}\).
Nápověda 4
Uvědomte si, že pro neideální dipól platí
\[\vec p = q\vec{d} .\]Jestliže vektor polarizace \(\vec{P}\) má význam hustoty dipólů a tento vektor je konstantní, celkový dipólový moment válce je
\[\vec p = V\vec{P}.\]Vyjádřete vztah mezi vektory \(\vec{P}\) a \(\vec{d}\)!
Řešení — pole uvnitř válce
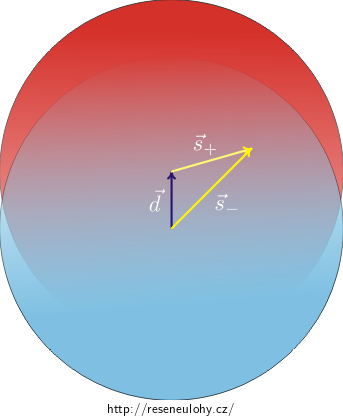
Jak bylo uvedeno v dřívější nápovědě: představte si válec jako dva válce vyplněné rovnoměrně kladným a záporným nábojem. Uvnitř válce s konstantní hustotou objemového náboje ρ je elektrické pole, jehož intenzita má radiální směr. Proto pokud označíme \(\vec{s}\) vektor spojující střed válce a dané místo (viz obrázek níže), můžeme psát
\[\vec E = \frac{\varrho}{2\varepsilon_0}\vec{s}.\]Polarizace způsobí „mírný posun kladného a záporného válce“, jejich osy se od sebe vzdálí o nepatrnou vzdálenost d, přičemž ale můžeme předpokládat, že posun je tak nepatrný, že při něm nedojde ke změně rozložení náboje. Potom pole uvnitř je superpozicí polí „kladného a záporného válce“ v daném místě, které je se středem kladného válce spojeno vektorem \(\vec{s}_+\) a se středem záporného válce vektorem \(\vec{s}_-\) (vektory jsou orientovaný ze středu válců). Označíme \(\vec{E}_+\), resp. \(\vec{E}_-\) příspěvek kladného, resp. záporného válce k elektrickému poli. Z principu superpozice vyplývá
\[\vec{E} = \vec{E}_+ + \vec{E}_- = \frac{\varrho}{2\varepsilon_0}(\vec{s}_+-\vec{s}_-) = -\frac{\varrho}{2\varepsilon_0}\vec d.\]
Platí ale, že
\[\vec P = \frac{\vec{p}}{V} = \frac{Q\vec{d}}{V} = \varrho\vec{d},\]kde Q je celkový náboj jednoho z válců a V je jeho objem. U vektoru \(\vec{d}\) je znaménko minus, neboť vektor \(\vec{d}\) na našem obrázku míří ze středu kladného válce do středu válce záporného, tedy od kladného náboje k zápornému; ve vztahu pro dipólový moment to však musí být opačně.
Proto se uvnitř válce vytvoří homogenní pole o intenzitě
\[\vec E = -\frac{\vec P}{2\varepsilon_0}.\]Nápověda 5
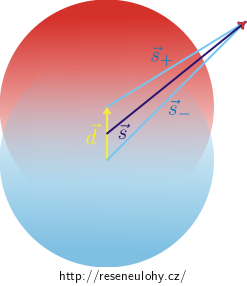
Při výpočtu pole vně polarizovaného válce uvažte symetrické posunutí kladného a záporného válce vůči středu původního. Vyšetřované místo prostoru spojte vektory
\(\vec{s}\) se středem původního válce,
\(\vec{s}_+\) se středem kladného válce,
\(\vec{s}_-\) se středem záporného válce.
Uvažte, že platí
\[\vec{s}_\pm = \vec{s}\ \mp\ \vec{d}/2,\]a tudíž
\[s_\pm^2 = \vec{s}_\pm \cdot \vec{s}_\pm = s^2 \mp \vec s\cdot\vec{d} + d^2/4\]a proveďte aproximace do prvního řádu v proměnné d.
Nápověda 6
Ukažte, že pro aproximaci do prvního řádu v proměnné d platí
\[\frac{\vec s_\pm}{s_\pm^2} \approx \frac{1}{s^2}\left(\vec s\pm \vec s\frac{\vec s\cdot\vec d}{s^2}\mp \frac{\vec d}{2}\right).\]Při provádění aproximací ihned zanedbávejte členy druhého řádu a vyššího a využijte vztah
\[\frac{1}{1+x} \approx 1-x, \qquad x\ll 1.\]Řešení — pole vně válce

Vně použijeme obdobný postup jako pro vnitřek válce: Gaussova věta pro válec s objemovým nábojem konstantní hustoty ρ dává v jeho okolí radiální pole o intezitě
\[\vec E = \frac{\varrho a^2}{2\varepsilon_0}\frac{\vec s}{s^2}\]ve vzdálenosti s od osy válce. Proto
\[\vec E = \vec E_+ + \vec E_- = \frac{\varrho a^2}{2\varepsilon_0}\left(\frac{\vec s_+}{s_+^2}-\frac{\vec s_{-}}{s_{-}^2}\right),\tag{1}\]kde \(\vec{s}_\pm = \vec{s} \mp \frac{\vec{d}}{2}\). Nyní provedeme aproximaci do prvního řádu v členu d výrazu v závorce:
\[\frac{\vec s_\pm}{s_\pm^2} = \left(\vec s\mp \frac{\vec d}{2}\right)\left(s^2+\frac{d^2}{4}\mp \vec s\cdot \vec d\right)^{-1} \approx.\]Nejprve zanedbáme člen s d2 v druhé závorce
\[\approx \left(\vec s\mp \frac{\vec d}{2}\right)\left(s^2\mp \vec s\cdot \vec d\right)^{-1} \approx,\]poté vytkneme z druhé závorky s-2 a použijeme vztah (1+x)-1 ≈ (1–x)
\[\approx \frac{1}{s^2}\left(\vec s\mp \frac{\vec d}{2}\right)\left(1\pm \frac{\vec s\cdot \vec d}{s^2}\right) \approx\]a nakonec roznásobíme závorky a zanedbáme člen řádu d2
\[\approx \frac{1}{s^2}\left(\vec s\pm \vec s\frac{\vec s\cdot\vec d}{s^2}\mp \frac{\vec d}{2}\right).\]Použitím této aproximace dostáváme
\[\left(\frac{\vec s_+}{s_+^2}-\frac{\vec s_-}{s_-^2}\right) \approx \frac{1}{s^2}\left(2\vec s\frac{\vec s\cdot \vec d}{s^2}-\vec d\right).\]S přihlédnutím k výše odvozenému vztahu (1) pro intenzitu elektrického pole vně válce a ke vztahu
\[\vec d = \frac{\vec P}{\varrho}\]dostaneme
\[\vec E(\vec s) = \frac{a^2}{2\varepsilon_0}\frac{1}{s^2}\left[\frac{2(\vec P\cdot \vec s)\vec s}{s^2}-\vec P\right].\]Výsledky
Uvnitř homogenně polarizovaného válce je homogenní pole a pro jeho intenzitu platí
\[\vec E = -\frac{\vec P}{2\varepsilon_0}.\]Vně homogenně polarizovaného válce je elektrické pole o intenzitě
\[\vec E = \frac{a^2}{2\varepsilon_0}\frac{1}{s^2}\left[\frac{2(\vec P\cdot \vec s)\vec s}{s^2}-\vec P\right],\]kde \(\vec{s}\) míří do daného místa od paty kolmice spuštěné do osy válce.
Komentář — jiné způsoby řešení
Úlohu lze, kromě výše popsaného způsobu, řešit také jinak, a to přímou integrací. Pokud si uvědomíme, že polarizace \(\vec{P}\) není nic jiného než „hustota dipólů“, a tudíž výpočet potenciálu vně válce lze provést přímou intergací potenciálu „jednotlivých dipólů“:
\[\varphi(\vec r) = \frac{1}{4\pi\varepsilon_0}\int_\mathrm{valec} \frac{\vec P\cdot(\vec r-\vec r^,)}{|\vec r-\vec r^,|^3}\,dV^.\]Pokud se jedná o homogenně polarizovaný válec, pak lze navíc vektor \(\vec{P}\) vytknout před integrál, který pak je formálně shodný s integrálem pro výpočet intenzity elektrického pole válce s objemovou hustotou náboje ρ = 1. Tímto postupem je řešena podobná úloha Pole homogenně polarizované koule.
Odkaz na podobnou úlohu


