Vodivé kolejnice
Úloha číslo: 410
Dvě dlouhé, rovnoběžné a dokonale vodivé kolejnice jsou od sebe vzdálené 50 cm a jsou umístěny v homogenním magnetickém poli o magnetické indukci 2 mT, které je kolmé k rovině kolejnic. Kolejnice jsou v jednom místě vodivě spojeny. Elektrický odpor spoje je 5 Ω. Po těchto kolejnicích klouže dokonale vodivá tyč konstantní rychlostí 2 m s-1. Určete:
a) velikost indukovaného napětí ve vodivé tyči, hodnotu a směr indukovaného elektrického proudu uzavřenou částí obvodu,
b) tažnou mechanickou sílu potřebnou k udržení dané rychlosti tyče a mechanický výkon této tažné síly.
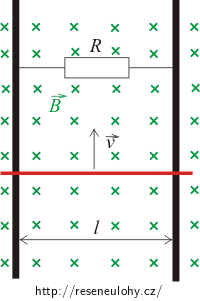
Poznámka: Mechanické efekty, jako je tření atd., při řešení úlohy zanedbejte.
Nápověda
Uvědomte si, kdy se ve vodivé smyčce indukuje napětí a jak toto napětí souvisí s magnetickým indukčním tokem.
Jestliže vodičem nacházejícím se v magnetickém poli prochází elektrický proud, působí na něj magnetická síla. Její směr určíme pomocí Flemingova pravidla levé ruky. Bude tato síla pohyb vodiče zrychlovat, nebo zpomalovat?
Flemingovo pravidlo levé ruky
Položíme-li k vodiči levou ruku tak, aby natažené prsty ukazovaly směr proudu a magnetické indukční čáry (respektive vektor \(\vec{B}\)) vstupovaly do dlaně, ukazuje odtažený palec směr a orientaci vektoru magnetické síly \(\vec{F}_\mathrm{m}\), která působí na vodič.
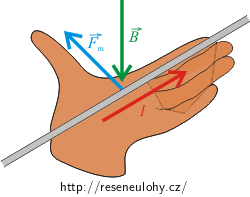
Rozbor
Vodivě spojené kolejnice a vodivá tyč vytvářejí smyčku. Ve smyčce se indukuje elektromotorické napětí, pokud se mění magnetický indukční tok plochou smyčky. Ten si můžeme představit jako „počet indukčních čar procházejících plochou smyčky“. Velmi důležité je, že indukované napětí nezáleží na celkovém „počtu indukčních čar“ procházejících plochou smyčky, ale pouze na „změně jejich počtu“. Tedy přesněji velikost indukovaného napětí, a tedy i proudu, závisí na rychlosti změny magnetického indukčního toku plochou uvnitř smyčky.
Pohybem vodivé tyče nahoru (viz obrázek) se zmenšuje plocha smyčky, a tedy i magnetický indukční tok plochou smyčky. V obvodu se indukuje proud, který kolem sebe vytváří magnetické pole. Magnetické indukční čáry tohoto pole budou mít takový směr, aby bránily změně magnetického toku, tj. budou ho chtít zvětšit. Jejich směr uvnitř smyčky tedy bude stejný jako směr vnějšího magnetického pole, tj. od nás (za obrázek). Pomocí Ampérova pravidla určíme směr indukovaného proudu, který bude po směru hodinových ručiček. Velikost elektrického proudu určíme z Ohmova zákona.
Na pohybující se vodič s proudem v magnetickém poli působí magnetická síla. Její směr určíme pomocí Flemingova pravidla levé ruky. Zjistíme, že směr této síly je přesně opačný, než jaký je směr vektoru rychlosti, tj. magnetická síla pohyb vodiče zpomaluje. Což jsme mohli odhadnout i přímo z toho, že síla působí proti příčině indukce elektrického proudu, tj. působí proti pohybu vodiče. Abychom udrželi konstantní rychlost pohybujícího se vodiče, musí na něj působit ještě jiná síla opačným směrem. V našem případě je to síla mechanická, která bude mít stejnou velikost jako magnetická síla, ale opačný směr.
Výkon mechanické síly určíme z definice výkonu – jako práci, kterou vykoná mechanická síla, dělenou potřebným časem.
Řešení a)
Určení indukovaného napětí
Indukované elektromotorické napětí se rovná změně magnetického indukčního toku Φ plochou smyčky za čas Δt:
\[U_\mathrm{i}=-\frac{\mathrm{\Delta} \Phi}{\mathrm{\Delta}t}.\tag{1}\]Pro indukční tok platí:
\[\Phi =B S\,\cos {\alpha},\]kde α je úhel mezi kolmicí k ploše smyčky a indukčními čarami, v našem případě α = 0°, tj. cos α = 1. A protože velikost magnetické indukce B je konstantní, platí pro změnu magnetického indukčního toku ΔΦ:
\[\mathrm{\Delta}\Phi = B\mathrm{\Delta}S,\]kde změna obsahu plochy ΔS je rovna
\[\mathrm{\Delta}S= - lv \mathrm{\Delta}t,\]znaménko mínus vyplývá z toho, že se plocha smyčky zmenšuje.
Výraz pro změnu magnetického indukčního toku dosadíme do rovnice (1) pro indukované elektromagnetické napětí Ui:
\[U_\mathrm{i}=-\frac{-Blv \mathrm{\Delta}t}{\mathrm{\Delta}t}= Blv \,\frac{\mathrm{\Delta}t}{\mathrm{\Delta}t}= Blv.\]Určení velikosti a směru indukovaného proudu
Velikost indukovaného proudu v uzavřené části obvodu určíme z Ohmova zákona, kde za napětí dosadíme velikost indukovaného napětí Ui a za elektrický odpor vodivého spojení kolejnic R (kolejnice jsou dokonale vodivé, to znamená, že jejich odpor můžeme zanedbat stejně jako odpor pohyblivé spojovací tyče):
\[U_\mathrm{i}=R I \,\,\,\Rightarrow\,\,\,I=\frac{U_\mathrm{i}}{R}.\]Po dosazení vztahu pro indukované napětí Ui, dostáváme pro velikost indukovaného proudu vztah:
\[I=\frac{Blv}{R}.\tag{2}\]Směr indukovaného elektrického proudu určíme pomocí Ampérova pravidla. Vztyčený palec nastavíme do směru magnetických indukčních čar magnetického pole vytvořeného vodičem s proudem. Podle Lenzova zákona má vektor \(\vec{B}_\mathrm{i}\) tohoto pole uvnitř smyčky stejný směr jako vektor vnějšího magnetického pole \(\vec{B}\), aby kompenzoval zmenšování magnetického indukčního toku smyčkou. Zahnuté prsty pak ukazují směr proudu ve vodiči. Z obrázku vidíme, že proud bude téci po směru hodinových ručiček.
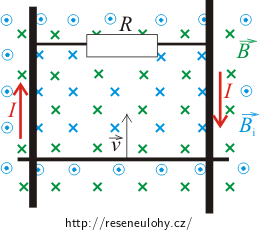
Poznámka: Zeleně je na obrázku naznačeno vnější magnetické pole, modře magnetické pole smyčky.
Řešení b)
Určení mechanické síly
Na vodič s proudem v magnetickém poli působí magnetická síla o velikosti:
\[F_\mathrm{m}=BIl \sin{\alpha},\]kde úhel α je úhel mezi vektorem magnetické indukce a směrem proudu. V našem případě je vektor magnetické indukce kolmý k vodiči s proudem a tedy úhel α = 90° a pro velikost magnetické síly Fm platí:
\[F_\mathrm{m}=BIl.\]Směr magnetické síly určíme pomocí Flemingova pravidla levé ruky. Zjistíme, že směr této síly je opačný, než jaký je směr rychlosti, tj. magnetická síla pohyb vodiče zpomaluje. Abychom udrželi konstantní rychlost pohybujícího se vodiče, musí na něj působit ještě jiná síla opačným směrem. V našem případě je to mechanická síla \(\vec{F}\), která bude mít stejnou velikost jako magnetická síla \(\vec{F}_\mathrm{m}\), ale opačný směr, tj. pro její velikost platí:
\[F=F_\mathrm{m}=BIl.\]Za hodnotu proudu I dosadíme vztah (2) vyjádřený v předchozím oddíle:
\[I=\frac{Blv}{R}.\]Pro velikost mechanické síly tak dostáváme vztah:
\[F=\frac{B^2l^2v}{R}.\tag{3}\]Určení výkonu mechanické síly
Výkon P je definován jako podíl práce W vykonané za daný čas t:
\[P=\frac{\mathrm{\Delta}W}{\mathrm{\Delta}t}.\]Práci W si můžeme vyjádřit jako sílu F působící po nějaké dráze Δs:
\[P=\frac{F\mathrm{\Delta}s}{\mathrm{\Delta}t}.\]Velikost rychlosti v je definována jako změna dráhy za čas, tedy \(\frac{\mathrm{\Delta}s}{\mathrm{\Delta}t}\). Výkon P si vyjádříme jako:
\[P=Fv,\]kde za velikost síly F dosadíme ze vzorce pro sílu (3) a dostáváme tak, že pro výkon mechanické síly \(\vec{F}\) platí:
\[P=\frac{(Blv)^2}{R}.\]Zápis a číselné dosazení
\(l = 50\,\mathrm{cm}=0{,}50\,\mathrm{m}\) vzdálenost kolejnic \(R=5\,\mathrm{\Omega}\) elektrický odpor spoje mezi kolejnicemi \(B=2{\cdot}10^{-3}\,\mathrm{T}\) magnetická indukce pole, které je kolmé k rovině kolejnic \(v=2\,\mathrm{ms^{-1}}\) rychlost, kterou klouže tyč po kolejnicích \(|U_\mathrm{i}|=?\,\mathrm{(V)}\) velikost indukovaného napětí ve vodivé tyči \(I=?\,\mathrm{(A)} \) velikost indukovaného elektrického proudu \(F=?\,\mathrm{(N)} \) tažnou mechanickou sílu potřebnou k udržení dané rychlosti tyče \(P=?\,\mathrm{(W)} \) mechanický výkon tažné síly
\[|U_\mathrm{i}|=Blv=2{\cdot}10^{-3}\cdot0{,}5{\cdot}2\,\mathrm{V}=2{\cdot}10^{-3}\,\mathrm{V}=2\,\mathrm{mV}\] \[I=\frac{Blv}{R}=\frac{2{\cdot}10^{-3}\cdot0{,}5{\cdot}2}{5}\,\mathrm{A}=0{,}4{\cdot}10^{-3}\,\mathrm{A}=0{,}4\,\mathrm{mA}\] \[F=\frac{B^2l^2v}{R}=\frac{(2{\cdot}10^{-3})^2{\cdot}0{,}50^2{\cdot}2}{5}\,\mathrm{N}=4{\cdot}10^{-7}\,\mathrm{N}=0{,}4\,\mathrm{\mu N}\] \[P=\frac{(Blv)^2}{R}=\frac{(2{\cdot}10^{-3}\cdot0{,}50{\cdot}2)^2}{5}\,\mathrm{W}=8{\cdot}10^{-7}\,\mathrm{W}=0{,}8\,\mathrm{\mu W}\]Odpověď
Ve vodivé tyči se při jejím pohybu po kolejnicích indukuje napětí o velikosti Ui = 2 mV a elektrický proud o velikosti I = 0,4 mA. Indukovaný proud teče po směru hodinových ručiček.
Pro udržení dané rychlosti tyče je potřeba na tyč působit mechanickou silou o velikosti F = 0,4 μN. Výkon této tažné síly je P = 0,8 μW.




