Sbírka řešených úloh

Magnetická indukce uvnitř toroidu

Úloha číslo: 442

Určete vztah pro velikost magnetické indukce uvnitř cívky ve tvaru toroidu, jehož šířka je podstatně menší než délka střední kružnice. Toroid má N_l závitů na jednotku délky a prochází jím elektrický proud I.

• Nápověda - Co je to toroid

  Cívka ve tvaru toroidu je vlastně solenoid (dlouhá úzká hustě vinutá cívka) stočená do tvaru prstence. Průběh magnetického pole toroidu odhadněte z pole solenoidu, viz úloha Magnetické pole solenoidu.

• Nápověda - Ampérův zákon

  Ampérův zákon se používá k výpočtu velikosti vektoru magnetické indukce \(\vec{B}\) v některých symetrických případech podobně, jako se používá Gaussova věta k výpočtu velikosti vektoru elektrické intenzity \(\vec{E}\) v symetrických případech v elektrostatice.

  Matematická podoba Ampérova zákona je

  \[\oint_\mathrm{l} \vec{B}\cdot \,\mathrm{d}\vec{l}=\mu_\mathrm{0} I_\mathrm{c},\]

  kde I_c značí celkový proud procházející plochou Ampérovy smyčky délky l.

• Rozbor

  Magnetickou indukci uvnitř toroidu určíme pomocí magnetického pole solenoidu, protože toroid můžeme charakterizovat jako solenoid stočený do tvaru prstence. Indukční čáry uvnitř toroidu tvoří soustředné kružnice. Pole uvnitř toroidu je homogenní a vně toroidu nulové.

  

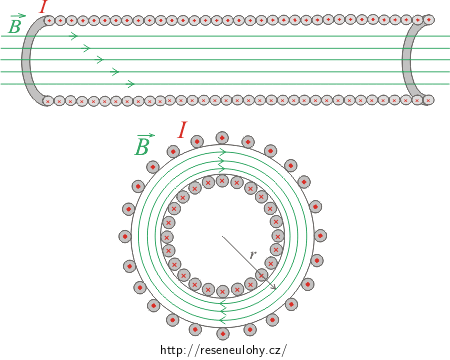
  Směr magnetické indukce je určen pravidlem pravé ruky. Vybereme si jednu kruhovou indukční čáru o poloměru r jako Ampérovu křivku a projdeme ji ve směru otáčení hodinových ručiček.

• Řešení

  Určení vztahu pro velikost magnetické indukce

  Z tvaru solenoidu můžeme usuzovat na to, že magnetické indukční čáry vektoru \(\vec{B}\) jsou soustředné kružnice uvnitř toroidu. Magnetické pole vně je nulové.

  

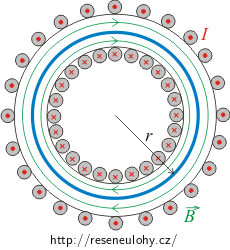
  Velikost vektoru magnetické indukce určíme z Ampérova zákona (viz nápověda), který má tvar

  \[\int_\mathrm{l} \vec{B}\cdot \,\mathrm{d}\vec{l}=\mu_\mathrm{0} I_\mathrm{c}.\]

  Jako Ampérovu křivku zvolíme kružnici o poloměru r se středem ve středu toroidu procházející vnitřkem toroidu (na obrázku je vyznačena modře). Její délka je

  \[l=2\pi r.\]

  Celkový proud procházející plochou kruhu, jehož hranici tvoří Ampérova křivka, je

  \[I_\mathrm{c}=N_\mathrm{l} lI=2\pi rN_\mathrm{l} I.\]

  Zde jsme využili toho, že šířka toroidu je mnohem menší než délka jeho střední kružnice (viz zadání).

  Vektor magnetické indukce \(\vec{B}\) je rovnoběžný s vektorem délkového elementu \(\mathrm{d}\vec{l}\) podél celé integrační cesty. Pravou stranu Ampérova zákona tak můžeme vyjádřit jako

  \[\int_\mathrm{l} \vec{B}\cdot \,\mathrm{d}\vec{l}=\int_\mathrm{l} B\,\mathrm{d}l=B\int_\mathrm{l}\,\mathrm{d}l=B\,2\pi r.\]

  Pravou a levou stranu Ampérova zákona porovnáme a vyjádříme hledanou velikost magnetické indukce B:

  \[B2\pi r=2\pi\mu_\mathrm{0} rN_\mathrm{l} I,\] \[B=\mu_\mathrm{0}N_\mathrm{l} I.\]

  Poznámka: Uvedený vztah platí za předpokladu, že studujeme magnetické pole ve vakuu. V případě, že toroid je vyplněn látkou, je ve vztahu permeabilita vakua μ₀ nahrazena permeabilitou μ dané látky:

  \[\mu =\mu_\mathrm{r}\mu_\mathrm{0}.\]

  Určení směru magnetické indukce

  Směr magnetické indukce uvnitř toroidu lze určit pomocí pravidla pravé ruky: Uchopíte-li toroid tak, aby prsty pravé ruky směřovaly ve směru proudu v závitech, pak vztyčený palec určuje směr magnetické indukce pole uvnitř toroidu.

• Odpověď

  Odvodili jsme vztah pro velikost vektoru magnetické indukce uvnitř toroidu:

  \[B=\mu_\mathrm{0}N_\mathrm{l} I.\]