Sbírka řešených úloh

Přímý dlouhý vodič v blízkosti kruhového závitu

Úloha číslo: 767

Přímým velmi dlouhým vodičem protéká proud I₁ = 3,14 A. Kruhovým závitem protéká proud I₂ = 3 A. Závit je umístěn tak, že jeho rovina je rovnoběžná s vodičem, a normála, vedená k rovině závitu jeho středem, vodič protíná. Vzdálenost středu závitu od vodiče je d = 20 cm, poloměr závitu R = 30 cm. Vypočtěte magnetickou indukci ve středu závitu.

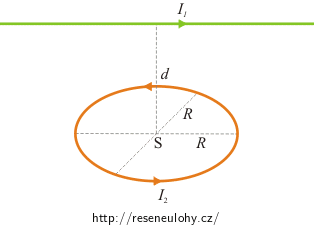
• Nápověda 1

  Zamyslete se nad rozmístěním vodičů. Řešení rozdělte na dvě části.

• Řešení nápovědy

  Vypočítáme zvlášť příspěvek od kruhového závitu a zvlášť příspěvek od přímého nekonečně dlouhého vodiče. Potom je vektorově sečteme.

• Nápověda 2

  Jak určíte směr magnetické indukce obou vodičů?

• Řešení nápovědy

  Využijeme Ampérovo pravidlo pravé ruky:

  Palec pravé ruky dáme tak, že ukazuje směr elektrického proudu ve vodiči. Pokrčené prsty pak ukazují orientaci magnetických indukčních čar v okolí přímého vodiče.

  Kruhový závit je vlastně přímý vodič stočený do smyčky. Jeho pole tvoří kružnice obklopující závit. Orientaci magnetických indukčních čar v bodě S určíme pomocí Ampérova pravidla pravé ruky.

• Řešení

  Magnetická indukce \(\vec B\) ve středu závitu je dána vektorovým součtem indukcí vyvolaných nekonečně dlouhým vodičem \(\vec B_1\) a závitem \(\vec B_2\):

  \[\vec B= \vec B_1+\vec B_2.\]

  Směry vektorů určíme pomocí Ampérova pravidla pravé ruky. Magnetická indukce přímého vodiče \(\vec {B_1}\) směřuje dozadu, směrem od nás, magnetická indukce kruhového závitu \(\vec {B_2}\) směřuje nahoru k přímému vodiči. Vektory magnetických indukcí jsou na sebe kolmé. Výslednice \(\vec B\) směřuje šikmo nahoru směrem od nás, jak vidíme na obrázku.

  

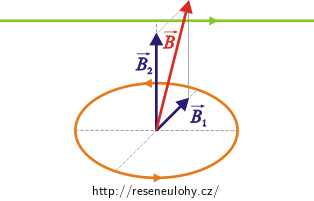
  Pro výpočet velikostí obou příspěvků použijeme vztahy odvozené v předchozích úlohách. V úloze Magnetické pole dlouhého přímého vodiče s proudem je odvozen vztah pro velikost magnetické indukce přímého vodiče B₁ a v úloze Magnetická indukce na ose kruhového závitu nalezneme vztah pro velikost magnetické indukce kruhového závitu B₂. Odtud víme, že

  \[ B_1 =\frac{\mu_0 I_1}{2 \pi d} \qquad \qquad B_2 = \frac{\mu_0 I_2}{2R}. \]

  Využijeme skutečnosti, že směry indukcí od přímého vodiče a od závitu jsou na  sebe kolmé, jak je vidět z obrázku výše. Pro velikost celkové magnetické indukce B pak můžeme pomocí Pythagorovy věty psát

  \[ B = \sqrt{B_1 ^{2} + B_2 ^{2}} = \frac{\mu_0}{2} \sqrt{\frac{I_1^2}{\pi^{2} d^{2}}+\frac{I_2^2}{R^{2}}}. \]

• Zápis a číselné dosazení

  I1 = 3,14 A	proud procházející přímým vodičem
  d = 20 cm = 0,2 m	vzdálenost přímého vodiče od středu S
  R = 30 cm = 0,3 m	poloměr závitu
  I2 = 3 A	proud procházející závitem
  B = ? (T)	velikost magnetické indukce
  Z tabulek:
  μ0 = 4π·10-7 Hm-1	permeabilita vakua

  ---

  \[ B = \frac{\mu_0}{2}\sqrt{\frac{I_1^2}{\pi^{2} d^{2}}+\frac{I_2^2}{R^{2}}} = \frac{4\pi \cdot 10^{-7}}{2} \cdot \sqrt{\frac{3{,}14^2}{\pi^{2}\cdot 0{,}2^{2}}+\frac{3^2}{0{,}3^{2}}}\,\mathrm T\,\dot{=}\, 7 \mu \mathrm T \]

• Odpověď

  Velikost celkové magnetické indukce ve středu závitu je přibližně 7 μT.