Indukované napětí při otáčení kruhové smyčky
Úloha číslo: 62
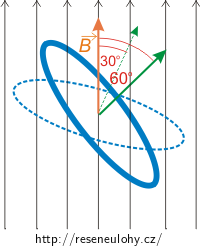
Magnetická indukce homogenního magnetického pole je 0,5 T. Rovina kruhové smyčky o poloměru 5 cm svírá se směrem indukce úhel 60°. Určete průměrnou velikost indukovaného napětí, jestliže se tento úhel za 0,02 s změní na 30°.
Nápověda
Uvědomte si, kdy se ve vodivé smyčce indukuje elektromotorické napětí a jak indukované napětí souvisí s magnetickým indukčním tokem.
Rozbor
Elektromotorické napětí se ve smyčce indukuje tehdy, když se mění magnetický indukční tok plochou smyčky. Magnetický indukční tok si můžeme představit jako „počet magnetických indukčních čar, které protnou plochu smyčky“. Úhel, který svírá magnetická indukce a smyčka, určujeme mezi směrem magnetické indukce a kolmicí k ploše smyčky. V našem případě svírá smyčka se směrem indukce úhel 60°. To znamená, že indukčních čar projde plochou smyčky méně, než kdyby smyčka svírala se směrem indukce nulový úhel.
Úhel mezi kolmicí k ploše smyčky a směrem indukce se změní z 60° na 30°. Tím se vlastně efektivně změní (zvětší) počet magnetických indukčních čár protínajících plochu. Ve smyčce se bude indukovat napětí.
Velikost elektromotorického napětí indukovaného ve vodivé smyčce je rovna změně magnetického indukčního toku za čas. Vypočítáme si tedy magnetické toky pro obě polohy smyčky, velikost jejich rozdílu a vydělíme je časem, za který se poloha smyčky změnila. Tím získáme průměrné indukované napětí.
Řešení
Jak již bylo uvedeno v rozboru, elektromotorické napětí se ve vodivé smyčce indukuje tehdy, když se mění magnetický indukční tok smyčkou. V našem případě se mění díky měnícímu se úhlu mezi plochou smyčky a směrem magnetické indukce.
Pro výpočet velikosti indukovaného napětí platí vztah:
\[|U_\mathrm{i}|=\left|\frac{\Delta \Phi}{\Delta t}\right|,\]kde za ΔΦ dosadíme velikost rozdílu toků v obou polohách.
Rozdíl hodnot píšeme do absolutních hodnot, protože nás zajímá pouze velikost indukovaného napětí:
\[|\Delta \Phi |= |\Phi_2 - \Phi_1|.\]Pro toky v jednotlivých polohách platí vztahy:
\[\Phi_1 = B S \,\cos \alpha_1= B \pi r^{2}\,\cos \alpha_1\] \[\,\] \[\Phi_2 = B S \,\cos \alpha_2= B \pi r^{2}\,\cos \alpha_2.\]Vztah dosadíme do vzorce pro elektromotorické napětí:
\[|U_\mathrm{i}|=\frac{|\Phi_2 - \Phi_1|}{\Delta t}=\frac{B\pi r^{2}|\cos \alpha_2 -\cos\alpha_1|}{\Delta t}.\]Zápis a číselné dosazení
\(B=\,0{,}5\,\mathrm{T}\) magnetická indukce pole \(r=\,0{,}05\,\mathrm{m}\) poloměr kruhové smyčky \(\alpha_1=\,60^{\mathrm{\circ}}\) úhel mezi rovinou smyčky a směrem indukce \(\alpha_2=\,30^{\mathrm{\circ}}\) úhel, který svírá rovina smyčky a směr indukce na konci \(\Delta t=\,0{,}02\,\mathrm{s}\) doba, po kterou se mění úhel, který rovina smyčky a směr indukce svírají \(U_\mathrm{i}=\mathrm{?}\,\mathrm{(V)}\) průměrná velikost indukovaného napětí během změny úhlu
\[U_\mathrm{i}=\frac{B\pi r^{2}\left|\cos 60^{\circ} -\cos30^{\circ}\right|}{\Delta t}=\frac{0{,}5\,\cdot\,\pi \,\cdot\,0{,}05^{2}\,\cdot\,\left|\frac{1}{2} -\frac{\sqrt{3}}{2}\right|}{ 0{,}02}\,\mathrm{V}=0{,}07\,\mathrm{V} \]Odpověď
Průměrná velikost napětí, které se indukuje ve vodivé smyčce, je Ui = 0,07 V.
Komentář - Průběh indukovaného napětí při rovnoměrném otáčení
Budeme předpokládat, že se cívka rovnoměrně otáčí z polohy 1 do polohy 2. Naším cílem bude určit průběh indukovaného napětí, nikoli pouze jeho průměrnou hodnotu.
Úhel mezi kolmicí k ploše a indukčními čarami α se mění s časem t podle vztahu:
\[\alpha =\varphi_0 - \omega t,\]kde φ0 je počáteční úhel otočení, v našem případě: \[\varphi_0 =\frac{\pi}{3}.\]
Úhlovou rychlost ω musíme zvolit tak, aby pro čas t = 0,02 s platilo:
\[\alpha = \varphi_0 - \,\omega t = \frac{\pi}{6}. \]Vyjádříme velikost úhlové rychlosti ω:
\[ \frac{\pi}{6}= \frac{\pi}{3}-0{,}02\,\omega \hspace{15px}\Rightarrow\hspace{15px}\omega = \frac{\pi}{6{\cdot}0{,}02}\,\mathrm{s^{-1}}.\]Pro magnetický indukční tok platí vztah:
\[\Phi= BS\cos(\varphi_0 -\omega t).\]Velikost elektromotorického napětí indukovaného ve vodivé smyčce je rovna rychlosti změny magnetického indukčního toku procházejícího plochou smyčky, tj.:
\[|U_\mathrm{i}|= \left|\frac{\mathrm{d}\Phi}{\mathrm{d}t}\right|.\]Jelikož nás zajímá pouze velikost indukovaného napětí, vystupují ve vztahu absolutní hodnoty.
Do tohoto vztahu dosadíme výraz pro magnetický indukční tok:
\[U_\mathrm{i}=\left|\frac{\mathrm{d}(BS \cos\,(\varphi_0−\omega t))}{\mathrm{d}t}\right|.\]Na čase t závisí pouze výraz cos(φ0−ωt), ostatní veličiny jsou konstanty nezávisející na čase a můžeme je napsat před derivaci:
\[U_\mathrm{i}=\left|BS\frac{\mathrm{d}}{\mathrm{d}t}(\cos\,(\varphi_0-\omega t))\right|.\]Jelikož jde o složenou funkci, vynásobíme mezi sebou derivaci vnitřní funkce (φ0−ωt) a derivaci vnější funkce (cos):
\[U_\mathrm{i}=\left|BS(-\omega)(-\sin\,(\varphi_0-\omega t))\right|.\]Upravíme a odstraníme absolutní hodnotu, protože všechny proměnné ve vzorci jsou kladné:
\[U_\mathrm{i}=BS\omega \sin\,(\varphi_0-\omega t).\]Po dosazení číselných hodnot pro t = 0 s do rovnice pro indukované napětí Ui dostáváme:
\[U_\mathrm{i} = 0{,}5 \cdot\pi\cdot 0{,}05^{2} \cdot \frac{\pi}{6{\cdot}0{,}02}\cdot \sin\frac{\pi}{3} = \frac{0{,}5 \cdot\pi^{2}\cdot 0{,}05^{2}}{0{,}12} \,sin \,\frac{\pi}{3}\] \[U_\mathrm{i} =0{,}09\,\mathrm{V}.\]Po dosazení číselných hodnot pro t = 0,02 s do rovnice pro indukované napětí Ui dostáváme:
\[U_\mathrm{i} = 0{,}5 \cdot\pi\cdot 0{,}05^{2} \cdot \frac{\pi}{6{\cdot}0{,}02}\cdot \sin\left(\frac{\pi}{3} - \frac{\pi}{6{\cdot}0{,}02}\cdot 0{,}02\right) = \frac{0{,}5 \cdot\pi^{2}\cdot 0{,}05^{2}}{0{,}12} \,\sin \,\frac{\pi}{6}\] \[U_\mathrm{i} =0{,}05\,\mathrm{V}.\]Velikost napětí, které se indukuje ve vodivé smyčce, klesne z hodnoty Ui = 0,09 V na hodnotu Ui = 0,05 V.
Dynamický prvek
Následující aplet zobrazuje rotující kruhovou smyčku v magnetickém poli (černá úsečka uprostřed), dále je zobrazeno okamžité indukované napětí a magnetický indukční tok smyčkou. Pomocí posuvníků je možné nastavit poloměr kruhé smyčky a velikost magnetické indukce.
Úlohy pro práci s apletem
- Spusťte animaci a pozorujte velikost magnetický indukční tok. Pro jaké hodnoty úhlů je magnetický indukční tok největší? Zdůvodněte, proč je největší zrovna pro tyto úhly.
- Spusťte animaci a pozorujte velikost indukovaného napětí. Pro jaké hodnoty úhlů je indukované napětí největší? Zdůvodněte, proč je největší zrovna pro tyto úhly.
- Má magnetický indukční tok i indukované napětí maximální hodnotu ve stejném okamžiku? Vysvětlete.
- Uveďte aplet do původního nastavení (RESET) a nalezněte hodnotu maximální velikost indukovaného napětí. Zdvojnásobte magnetickou indukci a opět nalezněte maximální velikost indukovaného napětí. Vyzkoušejte pro více hodnot magnetické indukce. Určete jak souvisí \(U_i\) a B.
- Jak se změní indukované napětí, pokud poloměr smyčky zdvojnásobím? Oveřte pro několik hodnot poloměru podobně jako v předchozí úloze.


