Sériový RLC obvod
Úloha číslo: 73
Obvod střídavého proudu je tvořen sériovým spojením:
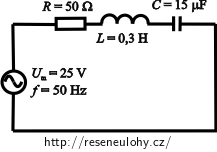
Zápis
Ze zadání si vypíšeme veličiny, které známe:
Odpor rezistoru R = 50 Ω Indukčnost cívky L = 0,3 H Kapacita kondenzátoru C = 15 μF =15·10-6 F Amplituda střídavého napětí na zdroji Um = 25 V Frekvence zdroje f = 50 Hz Zapojení rezistoru, cívky a kondenzátoru je sériové.Veličiny, které chceme získat:
Amplituda proudu v obvodu Im = ? (A) Fázový rozdíl mezi napětím a proudem v obvodu φ = ? (°) Rozbor úlohy
Postup řešení této úlohy:
- Vyjádříme si velikost amplitudy proudu. Použijeme Ohmův zákon pro střídavý proud, který vyjadřuje vztah mezi celkovou impedancí Z, amplitudou napětí na zdroji Um a amplitudou proudu Im. Pro tento výpočet známe všechny veličiny ze zadání.
- Protože jsou jednotlivé součástky zapojeny sériově, protéká všemi stejný proud, ale napětí na nich je fázově posunuto s proudem. Pro získání fázového rozdílu (posunu) mezi napětím a proudem využijeme fázorový diagram.
Postup kreslení fázorového diagramu
Fázorem nazýváme „šipku“, pomocí které do fázorového diagramu zakreslujeme napětí a proudy jednotlivých prvků zařazených v obvodu. Její velikost vyjadřuje amplitudu napětí nebo proudu a její směr vyjadřuje fázové posunutí.
Postup při kreslení fázorového diagramu pro sériový obvod:
Do fázorového diagramu znázorníme napětí a proud na jednotlivých prvcích střídavého obvodu.- Všemi součástkami v sériovém obvodu protéká stejný okamžitý proud, fázor proudu Im tedy bude společný a kreslí se obvykle v kladném směru osy x.
- Fázor napětí na rezistoru UR je rovnoběžný s fázorem proudu, protože fázový rozdíl mezi napětím a proudem je nulový — v případě rezistoru jsou napětí a proud ve fázi. Na obrázku je tento fázor zakreslen zeleně.
- Napětí na cívce UL „předbíhá“ proud o π/2 (čtvrt periody), a proto jeho fázor nakreslíme „nahoru“ — tedy v pomyslném kladném směru osy y. Uvažujeme totiž, že se fázory otáčejí proti směru hodinových ručiček. Na obrázku je tento fázor znázorněn žlutou barvou.
- Napětí na kondenzátoru UC se „zpožďuje“ za proudem o π/2, a proto jeho fázor nakreslíme „dolů“ — tedy v pomyslném záporném směru osy y. Tento fázor je zakreslen růžovou barvou.
- Amplitudu celkového napětí získáme „vektorovým součtem“ fázorů napětí na jednotlivých prvcích. Nejprve od sebe odečteme napětí na cívce UL a kondenzátoru UC (na obrázku naznačeno fialovou barvou). Pak tento rozdíl vektorově sečteme s napětím na rezistoru UR. Fázor amplitudy napětí celého obvodu je znázorněn světle modrou barvou.
- Fázovým rozdílem mezi napětím a proudem nazveme úhel φ, který svírají fázor proudu a fázor celkového napětí. Na obrázku je úhel φ znázorněn tmavě modrou barvou.
Pro RLC obvod se zadanými velikostmi veličin vypadá fázorový diagram takto:
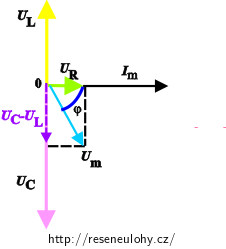
Nákresy fázorových diagramů v následujících oddílech již nejsou takto barevně zvýrazněné.
Odvození vzorce pro celkovou impedanci Z z fázorového diagramu
Chceme-li získat z fázorového diagramu celkovou impedanci Z, zakreslíme do fázorového diagramu místo jednotlivých napětí induktanci XL, kapacitanci XC a rezistanci R.
Z Ohmova zákona platí:
\[ U_\mathrm{C}=I_\mathrm{m} X_\mathrm{C}\mathrm{,}\hspace{20px}U_\mathrm{L}=I_\mathrm{m} X_\mathrm{L}\mathrm{,}\hspace{20px} U_\mathrm{R}=I_\mathrm{m} R\mathrm{.} \]Protože v sériovém obvodu protéká všemi součástkami stejný proud, vidíme, že impedance jednotlivých prvků jsou úměrné napětí, a proto pro ně můžeme nakreslit obdobný obrázek jako pro fázory napětí.
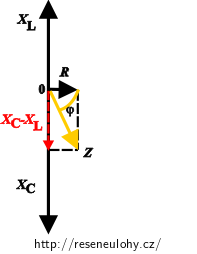
Pro výpočet impedance Z použijeme pravoúhlý trojúhelník, který vznikne při kreslení fázorového diagramu. Impedanci Z vyjádříme pomocí Pythagorovy věty
\[ Z^2=R^2+(X_\mathrm{C}-X_\mathrm{L})^2 \]nebo
\[ Z^2=R^2+(X_\mathrm{L}-X_\mathrm{C})^2 .\]Rozdíl mezi těmito vztahy je v tom, zda proud předbíhá napětí či se za napětím naopak zpožďuje. Velikost impedance Z tím ale není ovlivněna.
Po dosazení vztahů pro induktanci a kapacitanci dostaneme
\[ Z= \sqrt{R^2+(X_\mathrm{L}-X_\mathrm{C})^2}= \sqrt{R^2+\left({ \omega L- \frac{1}{\omega C}}\right)^2}. \]Vyjádření velikosti amplitudy proudu
Vzorec pro vyjádření impedance Z z Ohmova zákona zní \( Z=\frac{U_\mathrm{m}}{I_\mathrm{m}}=\sqrt{R^2+(\omega L-\frac{1}{\omega C})^2}. \)
Máme zjistit amplitudu proudu Im. Z předešlého vzorce ji můžeme snadno vyjádřit:
\[ I_\mathrm{m}=\frac{U_\mathrm{m}} {\sqrt{R^2+\left(\omega L-\frac{1}{\omega C}\right)^2}}. \]Vyjádření fázového rozdílu z fázorového diagramu
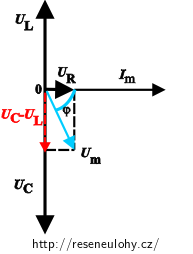

Fázový posun vyjádříme z fázorového diagramu obvykle ve tvaru:
\[ \mathrm{tg\,} \varphi = \frac{U_\mathrm{L}-U_\mathrm{C}}{U_\mathrm{R}} =\frac{I_\mathrm{m}\omega L- \frac{I_\mathrm{m}}{\omega C}}{I_\mathrm{m}R}=\frac{\omega L-\frac{1}{\omega C}}{R}= \frac{X_L-X_C}{R}\mathrm{.} \]Při kreslení fázorového diagramu a vyjadřování fázového posunu lze vzorec
\[ \mathrm{tg\,} \varphi = \frac{U_\mathrm{L}-U_\mathrm{C}}{U_\mathrm{R}}= \frac{X_\mathrm{L}-X_\mathrm{C}}{R} \]zaměnit za
\[ \mathrm{tg\,} \varphi = \frac{U_\mathrm{C}-U_\mathrm{L}}{U_\mathrm{R}}= \frac{X_\mathrm{C}-X_\mathrm{L}}{R}\mathrm{.} \]Pozor si musíme dát v interpretaci výsledku. V prvním případě čitatel zlomku říká, že uvažujeme případ, kdy napětí předbíhá proud (stejně jako na cívce). V druhém případě naopak napětí zaostává za proudem. Vhodný vztah použijeme buď podle nakresleného fázorového diagramu, kde vidíme fázový rozdíl mezi napětím a proudem, nebo si jeden z nich zvolíme a výsledek interpretujeme pomocí znaménka u výsledné hodnoty. Vybereme-li si například druhý vzorec pro vyjádření fázového posunu a výsledná hodnota nám vyjde se znaménkem plus, pak napětí opravdu zaostává za proudem. Pokud ovšem bude výsledná hodnota fázového posunu záporná, pak napětí předbíhá proud.
Číselné dosazení
Amplituda proudu:
\[ I_\mathrm{m}= \frac{U_\mathrm{m}}{\sqrt{R^2+\left(\omega L-\frac{1}{\omega C}\right)^2}}= \frac{25}{\sqrt {50^2+\left({2\pi \cdot 50 {\cdot} 0{,}3 - \frac{1}{2 \pi \cdot 50 {\cdot} 15 \cdot 10^{-6}}}\right)^2}}\,\mathrm{A} \,\dot{=}\, 0{,}2\,\mathrm{A}. \]Fázový posun můžeme vyjádřit pomocí impedancí:
\[ \mathrm{tg\,} \varphi = \frac{ \omega L- \frac{1}{ \omega C}}{R} = \frac{ 2 \pi \cdot 50 {\cdot} 0{,}3- \frac{1}{ 2 \pi \cdot 50 {\cdot} 15 \cdot 10^{-6} }}{50} \,\dot{=}\,-2{,}4. \]Nebo ho můžeme vyjádřit pomocí napětí na jednotlivých prvcích zařazených v obvodu.
Napětí na jednotlivých prvcích zařazených v obvodu jsou:
\[ U_\mathrm{R}=I_\mathrm{m}R\,\dot{=}\,0{,}2 {\cdot} 50\,\mathrm{V}=10\,\mathrm{V}\] \[U_\mathrm{L}=I_\mathrm{m} \omega L\,\dot{=}\, 0{,}2 {\cdot} 2 \pi \cdot 50 {\cdot} 0{,}3\,\mathrm{V}\dot= 18{,}85\,\mathrm{V}\] \[U_\mathrm{C}=\frac{I_\mathrm{m}}{\omega C}\,\dot{=}\,\frac{0{,}2}{2 \pi \cdot 50 {\cdot} 15 \cdot 10^{-6}}\,\mathrm{V}\dot= 42{,}44\,\mathrm{V}. \]Z fázového diagramu určíme velikost fázového rozdílu mezi napětím a proudem v obvodu:
\[ \mathrm{tg\,} \varphi=\frac{U_\mathrm{L}-U_\mathrm{C}}{U_\mathrm{R}}\dot= \frac{18{,}85-42{,}44}{10}\dot= -2{,}4. \]Oba způsoby nám daly stejný výsledek
\[ \varphi\, \dot{=} \, −67 ^\circ .\]Záporná hodnota říká, že se napětí zpožďuje za proudem.
Odpověď
Amplituda proudu v obvodu, ve kterém máme zapojen rezistor, cívku a kondenzátor sériově, má přibližně hodnotu 0,2 A.
Mezi napětím a proudem je fázový rozdíl asi φ = −67°.
Ze znaménka u hodnoty fázového rozdílu můžeme říci, že napětí se za proudem zpožďuje asi o 67° (protože se napětí za proudem zpožďuje, chová se zapojení jako kondenzátor).



