Elektron v obrazovce osciloskopu
Úloha číslo: 71
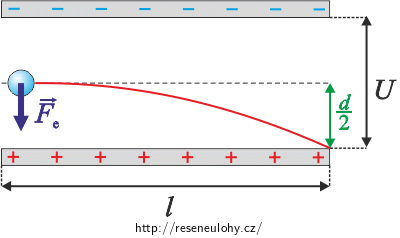
Elektron byl urychlen napětím 600 V. Pak vlétne doprostřed mezi vychylovací destičky obrazovky. Desky jsou od sebe vzdáleny 4 mm a jejich délka je 16 mm.
Při jakém vychylovacím napětí by elektron dopadl na konec vychylovací desky?
Nápověda 1
Nakreslete si obrázek celé situace. Jaká síla působí na elektron mezi deskami?
O jaký pohyb se jedná?
Obrázek
Nápověda 2
Zrychlení elektronu můžeme vyjádřit z druhého Newtonova zákona, do kterého dosadíme elektrickou sílu. Ta je přímo úměrná intenzitě elektrického pole a náboji elektronu.
Nápověda 3
Při urychlování vykoná zdroj napětí práci a tím dodá elektronu kinetickou energii. Vykonaná práce závisí na napětí zdroje a náboji elektronu.
Rozbor
Při urychlování elektronu napětím U zdroj tohoto napětí vykoná práci a elektron tak získá kinetickou energii. Z této energie můžeme zjistit rychlost, kterou elektron vlétne mezi vychylovací destičky.
Poté, co vlétne elektron mezi vychylovací desky, začne na něj kolmo na směr pohybu působit elektrická síla (viz obrázek). Situace je stejná jako když v gravitačním poli hodíme vodorovně například míček. Trajektorie elektronu bude tedy stejná jako při vodorovném vrhu, tj. bude jí parabola.
Pohyb elektronu můžeme rozdělit na dvě části:
- Rovnoměrný pohyb ve vodorovném směru rychlostí, kterou elektron vlétl mezi desky.
- Rovnoměrně zrychlený pohyb ve svislém směru způsobený elektrickou silou.
Z vodorovného pohybu určíme, jak dlouho se bude elektron pohybovat než dopadne na konec desky. Tento čas dosadíme do vztahu pro dráhu rovnoměrně zrychleného pohybu.
Ve vztahu pro dráhu ještě vystupuje zrychlení elektronu. To můžeme vyjádřit pomocí elektrické síly a druhého Newtonova zákona. Velikost elektrické síly je přímo úměrná intenzitě elektrického pole a náboji elektronu.
Intenzita elektrického pole roste s napětím na vychylovacích deskách a klesá s jejich vzdáleností.
Řešení: Rychlost, kterou elektron vlétne mezi desky
Při urychlování elektronu napětím U0 zdroj tohoto napětí vykoná práci a tím dodá elektronu kinetickou energii. Zdroj, který elektron urychluje, vykoná práci
\[W\,=\,QU_0\,.\]Protože urychlujeme elektron, můžeme dosadit velikost náboje tohoto elektronu:
\[W\,=\, eU_0\,.\]Vykonáním této práce získá elektron kinetickou energii:
\[E_\mathrm{k}\,=\, \frac{1}{2} m v_\mathrm{x}^2\,,\]kde m je hmotnost elektronu a vx je jeho rychlost po urychlení (před tím, než vlétne mezi vychylovací destičky).
Z těchto dvou vztahů vyjádříme rychlost vx, kterou vlétne elektron mezi desky:
\[E_\mathrm{k}\,=\, W,\] \[\frac{1}{2} m v_\mathrm{x}^2\,=\, eU_0,\] \[v_\mathrm{x}^2\,=\, \frac{2eU_0 }{m},\] \[v_\mathrm{x}\,=\,\sqrt{ \frac{2eU_0 }{m}}.\]Řešení: Zrychlení elektronu ve svislém směru
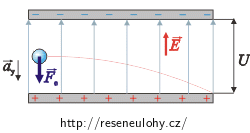
Ve svislém směru na elektron působí elektrická síla \(\vec{F}_\mathrm{e}\). Její velikost můžeme vyjádřit pomocí náboje elektronu a intenzity elektrického pole:
\[F_\mathrm{e} \,=\, e E.\]Intenzita homogenního elektrického pole mezi nabitými deskami je rovna
\[E\,=\, \frac{U}{d}\,.\]Elektrickou sílu tedy vyjádříme jako
\[F_\mathrm{e} \,=\, \frac{ e U}{d}\,.\tag{*}\]Zrychlení, které způsobuje elektrická síla, vypočítáme z druhého Newtonova zákona:
\[a_\mathrm{y}\,=\, \frac{F_\mathrm{e}}{m}.\]Dosazením za elektrickou sílu ze vzorce (*) získáme vztah pro zrychlení:
\[a_\mathrm{y}\,=\, \frac{\frac{ e U}{d}}{m},\] \[a_\mathrm{y}\,=\, \frac{ e U}{md }.\]Řešení: Výpočet napětí mezi deskami
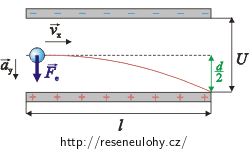
Jakmile vlétne elektron mezi desky, začne na něj působit směrem dolů elektrická síla Fe.
Pohyb elektronu mezi deskami můžeme rozdělit na dvě složky. Elektron letí vodorovně rovnoměrným pohybem rychlostí vx a zároveň směrem dolů se pohybuje rovnoměrně zrychleně se zrychlením ay.
Nyní si vyjádříme vzdálenost, kterou elektron urazí ve vodorovném a svislém směru.
Ve vodorovném směru přelétne elektron rovnoměrným pohybem celou desku o délce l:
\[l\,=\, v_x t.\]Za stejný čas t elektron ve svislém směru přelétne rovnoměrně zrychleně polovinu vzdálenosti desek, tj. vzdálenost \(\frac{d}{2}\):
\[\frac{d}{2}\,=\,\frac{1}{2}a_\mathrm{y} t^2.\]Z první rovnice vyjádříme čas t:
\[t\,=\, \frac{l}{v_\mathrm{x}}\]a dosadíme do druhé rovnice:
\[\frac{d}{2}\,=\,\frac{1}{2}a_y \frac{l^2}{v_\mathrm{x}^2}\,.\]Dosadíme za rychlost vx a zrychlení ay vztahy, které jsme si vyjádřili v předchozích oddílech:
\[\frac{d}{2}\,=\,\frac{1}{2}\, \frac{e U}{m d}\, \frac{l^2}{\frac{2 U_0 e}{m}}.\]Vzorec budeme postupně upravovat tak, abychom vyjádřili hledané napětí U:
\[d\,=\,\, \frac{ U}{ d}\, \frac{l^2}{2 U_0 },\] \[U\,=\,\, \frac{2 U_0 d^2}{l^2}.\]Pozn.: Pokud by bylo napětí U větší, byla by větší i elektrická síla a elektron by dopadl na destičku ještě před jejím koncem. Pokud by naopak bylo napětí menší, elektron by se sice od vodorovného směru odchýlil, ale ne dostatečně a mezi deskami prolétl.
Zápis a číselný výpočet
U0 = 600 V
d = 4 mm = 4·10−3 m
l = 16 mm = 1,6·10−2 m
U = ? (V)
\[U\,=\,\, \frac{2 U_0 d^2}{l^2}\,=\,\frac{2 \cdot\, 600 \cdot\, \left( 4 {\cdot} 10^{-3}\right)^2}{\left(1{,}6 {\cdot} 10^{-2}\right)^2}\,\mathrm{V}\] \[U\,=\,75\,\mathrm{V}\]Odpověď
Aby elektron dopadl na konec vychylovací desky, musí být vychylovací napětí
\[U\,=\,\, \frac{2 U_0 d^2}{l^2}\,=\,75\,\mathrm{V}\,.\]Obrazovka televize
Vychylování paprsku elektronů pomocí vychylovacích destiček se využívá například v obrazovkách osciloskopů. Úhel, o který mohou destičky vychýlit elektron, je poměrně malý. Proto je obrazovka osciloskopu malá a dlouhá.
V klasických televizních obrazovkách je paprsek vychylován pomocí magnetického pole soustavy cívek (princip je totožný jako vychýlení α částic v úloze Urychlená α částice).
(Pozn.: Plazmové a LCD obrazovky fungují na jiném principu.)
Porovnání elektrické a tíhové síly
Velikosti sil vypočítáme ze vztahů:
\[F_\mathrm{e}\,=\,\frac{eU}{d},\] \[F\,=\,mg\,.\]Dosadíme číselné hodnoty veličin:
e = 1,6·10−19 C,
U = 75 V,
d = 4·10−3 m,
m = 9,1·10−31 C.
Dostaneme:
\[F_\mathrm{e}\,=\,\frac{1{,}6{\cdot} 10^{-19}\,\cdot\,75}{4{\cdot} 10^{-3}}\,\mathrm{N}\,=\,3{\cdot} 10^{-15}\,\mathrm{N},\] \[F\,=\,9{,}1{\cdot} 10^{-31}\,\cdot\,10\,\mathrm{N}\,=\,9{,}1{\cdot} 10^{-30}\,\mathrm{N}.\]V této úloze je tíhová síla oproti elektrické síle menší o patnáct řádů, proto ji můžeme zanedbat.
Pokud bychom tíhovou sílu nemohli nebo nechtěli zanedbat, počítali bychom s tím, že ve svislém směru působí na elektron konstantní síla o velikosti Fe + FG. Úloha by tedy nebyla o mnoho komplikovanější.