Sbírka řešených úloh

Dvě žárovky

Úloha číslo: 236

• Nápověda 1

  Uvědomte si, co znamenají údaje vyznačené na žárovkách.

• Řešení nápovědy 1

  Údaje vyznačené na žárovkách jsou jmenovité hodnoty proudu a napětí. Pokud má mít žárovka jmenovitý příkon, musí jí procházet jmenovitý proud a být na ní jmenovité napětí.

• Nápověda 2

  Uvědomte si, jakým způsobem můžeme zapojit do obvodu dva spotřebiče. Co platí pro proudy, napětí a celkové odpory v obvodu?

• Řešení nápovědy 2

  Dva spotřebiče mohou být do obvodu zapojeny buď sériově, nebo paralelně.

  V úloze Řešení obvodu s rezistory v Řešení nápovědy najdete, co platí pro proudy, napětí a celkové odpory v těchto obvodech.

• Rozbor

  Příkon elektrického proudu se rovná součinu napětí na spotřebiči a proudu, který spotřebičem protéká. Chceme-li, aby spotřebič měl jmenovitý příkon, musí na tomto spotřebiči být jmenovité napětí a protékat jím jmenovitý proud (hodnoty uvedené výrobcem na spotřebiči).

  Dvě žárovky můžeme do obvodu zapojit buď sériově, nebo paralelně, a proto se pokusíme řešit úlohu dvojím způsobem.

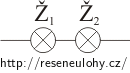
  Pro sériové zapojení platí, že celkové napětí v obvodu se rovná součtu napětí na jednotlivých spotřebičích. Celkový proud procházející obvodem je totožný s proudy, které procházejí jednotlivými spotřebiči. V této úloze se proudy, které mají procházet žárovkami, shodují, proto je můžeme zapojit sériově. Abychom na obou žárovkách získali požadované hodnoty napětí a proudu, přidáme do obvodu rezistor a určíme jeho odpor z podmínek pro napětí a proud při sériovém zapojení.

  

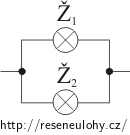
  Při paralelním zapojení je napětí ve všech větvích konstantní (tj. stejné jako napětí na zdroji) a součet proudů procházejících jednotlivými větvemi se rovná celkovému proudu. Do každé větve s žárovkou připojíme sériově rezistor. Z podmínek pro napětí a proud při paralelním zapojení vypočítáme odpor obou přidaných rezistorů.

  

• Řešení

  Dvě žárovky můžeme do obvodu zapojit sériově nebo paralelně.

  Aby obě žárovky měly jmenovitý příkon, musí mít jmenovité napětí a musí jimi protékat jmenovitý proud (hodnoty uvedené na žárovkách).

  Napětí na žárovkách ovlivníme vhodně přidanými rezistory a vypočítáme jejich odpory.

  Sériově zapojené žárovky

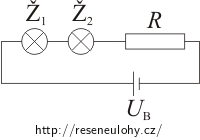
  K sériově zapojeným žárovkám přidáme rezistor, jak to ukazuje obrázek.

  

  Pro sériové zapojení platí, že celkový proud procházející obvodem je stejný jako proud, který prochází jednotlivými spotřebiči. Celkové napětí v obvodu se rovná součtu napětí na jednotlivých spotřebičích. Tedy:

  \[I\,=\,I_1\,=\,I_2\,=\,I_\mathrm{R}\] \[U_\mathrm{B}\,=\,U_1\,+\,U_2\,+\,U_\mathrm{R}\,,\]

  kde I je celkový proud procházející obvodem, I₁ a I₂ jsou proudy žárovkami Ž₁ a Ž₂, I_R je proud protékající rezistorem o odporu R; U_B je napětí na zdroji, U₁ a U₂ napětí na žárovkách a U_R je napětí na rezistoru.

  Z Ohmova zákona vypočítáme úbytek napětí na rezistoru:

  \[U_\mathrm{R}\,=\,RI_\mathrm{R}\,=\,RI_1\,.\]

  Pro napětí na zdroji tedy platí:

  \[U_\mathrm{B}\,=\,U_1\,+\,U_2\,+\,RI_1\,.\]

  Z tohoto vztahu si vyjádříme odpor rezistoru R:

  \[R\,=\,\frac{U_\mathrm{B}\,-\,\left(U_1\,+\,U_2\right)}{I_1}\,.\]

  Paralelně zapojené žárovky

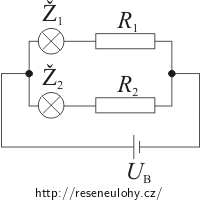
  K paralelně zapojeným žárovkám přidáme do každé větve jeden rezistor (viz obrázek).

  

  Při paralelním zapojení je napětí na všech větvích stejné:

  \[U_\mathrm{B}\,=\,U_\mathrm{x}\,=\,U_\mathrm{y}\,.\]

  U_B je napětí na zdroji, U_x je napětí ve větvi se žárovkou Ž₁ a U_y napětí ve větvi se žárovkou Ž₂.

  Protože žárovka a rezistor jsou v každé větvi zapojeny sériově, platí:

  \[U_\mathrm{x}\,=\,U_1\,+\,U_\mathrm{R1}\,=\,U_1\,+\,R_1I_1\,=\,U_\mathrm{B}\] \[U_\mathrm{y}\,=\,U_2\,+\,U_\mathrm{R2}\,=\,U_2\,+\,R_2I_2\,=\,U_\mathrm{B}\,.\]

  Nyní můžeme vyjádřit odpory R₁ a R₂ obou rezistorů:

  \[R_1\,=\,\frac{U_\mathrm{B}\,-\,U_1}{I_1}\] \[R_2\,=\,\frac{U_\mathrm{B}\,-\,U_2}{I_2}\,.\]

• Číselné dosazení

  Ze zadání úlohy víme:

  UB = 30 V	napětí na zdroji
  U1 = 3,5 V	údaje na žárovce Ž1
  I1 = 100 mA = 0,1 A
  U2 = 1,5 V	údaje na žárovce Ž2
  I2 = 0,1 A

  ---

  Sériové zapojení:

  

  Podle vztahu, který jsme získali v minulém oddílu, vypočítáme odpor přidaného rezistoru:

  \[R\,=\,\frac{U_\mathrm{B}\,-\,\left(U_1\,+\,U_2\right)}{I_1}\,=\,\frac{30\,-\,\left(3{,}5\,+\,1{,}5\right)}{0{,}1}\,\mathrm{\Omega}\,=\,250\,\mathrm{\Omega}\]

  Paralelní zapojení:

  

  Výpočet odporů přidaných rezistorů:

  \[R_1\,=\,\frac{U_\mathrm{B}\,-\,U_1}{I_1}\,=\,\frac{30\,-\,3{,}5}{0{,}1}\,\mathrm{\Omega}\,=\,265\,\mathrm{\Omega}\] \[R_2\,=\,\frac{U_\mathrm{B}\,-\,U_2}{I_2}\,=\,\frac{30\,-\,1{,}5}{0{,}1}\,\mathrm{\Omega}\,=\,285\,\mathrm{\Omega}\]

• Odpověď

  Žárovky můžeme zapojit buď sériově, nebo paralelně.

  Sériové zapojení:

  K žárovkám připojíme sériově rezistor R.

  

  Aby obě žárovky měly jmenovitý příkon, musí být odpor přidaného rezistoru 250 Ω.

  Paralelní zapojení:

  K žárovkám připojíme do každé větve jeden rezistor.

  

  Aby obě žárovky měly jmenovitý příkon, musí být odpory přidaných rezistorů R₁ = 265 Ω, R₂ = 285 Ω.

• Poznámka

  Úlohu bylo možné řešit dvojím způsobem díky vhodně zvoleným hodnotám napětí a proudů na žárovkách. Při různých hodnotách proudu by nebylo možné použít sériové zapojení.