Vodivá smyčka v magnetickém poli od dlouhého přímého vodiče
Úloha číslo: 375
Elektrický spotřebič o příkonu 110 W je připojen do elektrické sítě o efektivní hodnotě napětí 230 V a frekvenci 50 Hz. Jeden z přívodních kabelů je instalován tak, že jej můžeme považovat za nekonečně dlouhý přímý vodič. Ve vzdálenosti 10 cm od tohoto vodiče je umístněna vodivá smyčka o ploše 2 cm2, k jejíž rovině je kolmý vektor magnetické indukce \(\vec{B}\) magnetického pole vodiče.
a) Nakreslete obrázek celé situace.
b) Určete efektivní hodnotu elektrického proudu tekoucího přívodním vodičem.
c) Určete časový průběh magnetické indukce generovaný elektrickým proudem a maximální hodnotu magnetické indukce ve vzdálenosti 10 cm od vodiče, tj. v místě smyčky.
d) Určete časový průběh indukovaného napětí ve smyčce a maximální hodnotu indukovaného napětí.
Pozn.: Pro jednoduchost budeme předpokládat, že spotřebič má charakter rezistoru.
Řešení a) Poloha vodivé smyčky vůči vodiči s proudem
Magnetické indukční čáry charakterizující magnetické pole dlouhého přímého vodiče s proudem mají tvar soustředných kružnic rozložených v rovině kolmé k vodiči a se středem v místě průchodu vodiče.
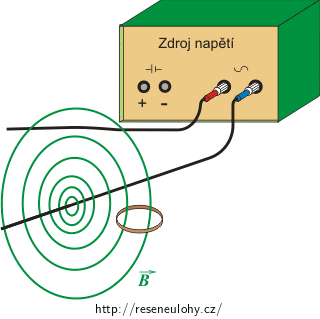
Směr vektoru magnetické indukce určíme pomocí pravidla pravé ruky, kdy naznačíme uchopení vodiče do pravé ruky tak, aby palec ukazoval směr proudu ve vodiči, prsty pak ukazují orientaci magnetických indukčních čar.
Protože vodičem prochází střídavý proud, směr proudu ve vodiči se mění, a tím se mění i směr vektoru magnetické indukce \(\vec{B}\).
Aby byl vektor magnetické indukce kolmý na plochu smyčky, musí být vodivá smyčka umístněna tak, jak je nakresleno na obrázku.
V obrázku není záměrně vyznačen směr proudu a není nakreslen ani vektor magnetické indukce \(\vec{B}\), protože se s časem mění.
Nápověda b) Efektivní hodnota proudu
Uvědomte si, jak spolu souvisí výkon stejnosměrného proudu a výkon střídavého proudu, tj. jak jsou definovány efektivní hodnoty proudu a napětí.
Protože spotřebič má charakter rezistoru, je účiník ve výpočtu výkonu střídavého proudu nulový.
Nápověda c) Magnetické indukce
Při určení vztahu pro časový průběh magnetické indukce využijte vztahu pro velikost magnetické indukce B ve vzdálenosti d od dlouhého přímého vodiče s proudem I:
\[B=\frac{\mu_0}{2\pi}\frac{I}{d}.\]Jestliže vodičem prochází střídavý proud, okamžitá hodnota proudu se mění s časem. Závislost okamžité hodnoty proudu na čase popisujeme pomocí goniometrické funkce – sinus nebo kosinus.
Nápověda d) Indukované napětí
Pro určení časového průběhu indukovaného napětí ui(t) vyjdeme z Faradayova zákona elektromagnetické indukce:
\[u_\mathrm{i}(t)=-\frac{\,\mathrm{d}\Phi}{\,\mathrm{d}t}.\]Vzhledem k tomu, že smyčka je relativně malá, budeme uvažovat stejnou magnetickou indukci \(\vec{B}\) v celé její ploše. Magnetický indukční tok Φ plochou smyčky S je potom dán vztahem:
\[\Phi=BS \cos {\alpha},\]kde α představuje úhel mezi normálou plochy smyčky S a vektorem magnetické indukce \(\vec{B}\).
Rozbor
Určení efektivní hodnoty elektrického proudu
Efektivní hodnota střídavého proudu je rovna velikosti stejnosměrného proudu, který má v obvodu s rezistorem stejný výkon jako střídavý proud. Totéž platí i pro efektivní hodnotu napětí. Vyjádříme si tedy výkon jako součin efektivního proudu a efektivního napětí, jehož hodnota je 230 V. Ze vztahu pak vyjádříme efektivní hodnotu proudu.
Určení průběhu magnetické indukce
Jestliže vodičem prochází střídavý proud, začne se v jeho okolí vytvářet časově proměnné magnetické pole, které charakterizujeme elektromagnetickou indukcí. Okamžitá velikost elektromagnetické indukce je úměrná velikosti okamžitého proudu, který vodičem prochází, a zároveň klesá se vzdáleností od vodiče.
Určení průběhu indukovaného napětí
Indukované elektromagnetické napětí ve smyčce vzniká díky měnící se elektromagnetické indukci. Je úměrné časové změně celkového magnetického toku plochou uvnitř smyčky. Matematicky popisuje tuto závislost tzv. Faradayův zákon elektromagnetické indukce.
Magnetický indukční tok plochou si můžeme představit jako „tok“ siločar, které plochou procházejí. Pro malé smyčky, u kterých můžeme předpokládat, že magnetická indukce je stejná v celé jejich ploše, je magnetický tok plochou dán součinem velikosti magnetické indukce („počtu siločar“) a obsahem plochy smyčky.
Řešení b) Určení efektivní hodnoty elektrického proudu
Efektivní hodnota střídavého proudu I je hodnota odpovídající stejnosměrnému proudu Ist, který má v obvodu s rezistorem stejný výkon jako střídavý proud.
Pro výkon efektivního proudu I platí:
\[P=UI,\]kde U je efektivní hodnota střídavého napětí.
Odtud vyjádříme hledaný efektivní proud I:
\[I=\frac{P}{U}.\]Řešení c) Určení průběhu magnetické indukce
Velikost magnetické indukce B ve vzdálenosti d od přímého dlouhého vodiče, kterým protéká proud I, je popsána vztahem:
\[B=\frac{\mu_0}{2\pi}\frac{I}{d}.\]Protože nás zajímá časový průběh magnetické indukce B(t), dosadíme za proud I časový průběh proudu:
\[i=I_\mathrm{m} \cos {(\omega t)}.\]Poznámka: Proud ve vodiči je střídavý, jeho hodnoty se tedy periodicky mění. Pro zápis okamžité hodnoty elektrického proudu můžeme použít jak funkci sinus, tak funkci kosinus, které jsou vůči sobě jen posunuté o půl periody. Pro řešení jsme zvolili zápis okamžité hodnoty proudu pomocí funkce kosinus.
Veličina Im ve vztahu pro okamžitou hodnotu elektrického proudu je maximální hodnota elektrického proudu procházejícího vodičem. Platí pro ni:
\[I=\frac{I_\mathrm{m}}{\sqrt2}\,\,\,\,\Rightarrow\,\,\,\, I_\mathrm{m}=\sqrt2 I,\]kde I je efektivní hodnota střídavého proudu.
Velikost úhlové rychlosti ω vyjádříme pomocí frekvence f:
\[\omega=2\pi f.\]Dosadíme do vztahu pro časový průběh magnetické indukce a dostaneme:
\[B(t)=\frac{\mu_0}{2\pi d}\,\sqrt2 \,I \cos {(2\pi f t)}.\tag{1}\]Hodnota magnetické indukce v místě smyčky bude maximální, když
\[\cos {(2\pi f t)}=1.\]Pro maximální hodnotu magnetické indukce tedy platí:
\[B_\mathrm{max}=\frac{\sqrt2}{2}\,\frac{\mu_0 I}{\pi d}.\]Řešení d) Vztah pro indukované napětí
Elektromagnetické napětí ui(t) ve smyčce vzniká při změně magnetického indukčního toku smyčkou v čase. Matematický zápis tohoto vztahu je označován jako Faradayův zákon elektromagnetické indukce a zní:
\[u_\mathrm{i}(t)=-\frac{\,\mathrm{d}\Phi}{\,\mathrm{d}t}.\tag{2}\]Vzhledem k tomu, že smyčka je relativně malá, budeme uvažovat stejnou magnetickou indukci \(\vec{B}\) v celé její ploše. Magnetický indukční tok Φ plochou smyčky S je potom dán vztahem:
\[\Phi=BS \cos {\alpha},\]kde α představuje úhel mezi normálou plochy smyčky S a vektorem magnetické indukce \(\vec{B}\). V našem případě je magnetická indukce kolmá na plochu smyčky. Úhel je tedy α = 0°. Pro magnetický indukční tok plochou Φ tedy platí:
\[\Phi=BS \cos {0}=BS.\tag{3}\]Velikost magnetické indukce B se mění s časem podle vztahu (1) vyjádřeném v předchozím oddíle:
\[B(t)=\frac{\mu_0}{2\pi d}\,\sqrt2 \,I\,\cos {(2\pi f t)}.\]Pro magnetický indukční tok smyčkou tak podle rovnice (3) platí:
\[\Phi=\frac{\mu_0}{2\pi d}\,\sqrt2\,I\,\cos{(2\pi f t)}\,S.\]Výraz pro magnetický indukční tok dosadíme do rovnice (2) pro velikost indukovaného elektromagnetického napětí ui(t) a dostaneme:
\[u_\mathrm{i}(t)=-\frac{\,\mathrm{d}\Phi}{\,\mathrm{d}t},\] \[u_\mathrm{i}(t)=\frac{\mathrm{d}}{{\,\mathrm{d}t}}\left(-\frac{\mu_o}{2\pi d}\,\sqrt2\,SI\,\cos{(2\pi f t)}\right).\]Provedeme uvedenou derivaci. Na čase závisí pouze kosinus, vše ostatní jsou konstanty, které můžeme vytknout před derivaci:
\[u_\mathrm{i}(t)=-\frac{\sqrt2\mu_0}{2\pi d}\,SI\frac{\mathrm{d}}{{\,\mathrm{d}t}}\left(\cos(2\pi f t)\right),\] \[u_\mathrm{i}(t)=\frac{\sqrt2\mu_0}{2\pi d}\,SI\,2\pi f\,\sin(2\pi f t).\]Časový průběh indukovaného napětí ui(t) ve smyčce je pak dán vztahem:
\[u_\mathrm{i}(t)=\frac{\sqrt2\mu_0 f }{d} SI\,\sin {(2\pi ft)}.\]Hodnota indukovaného napětí bude maximální, jestliže:
\[\sin {(2\pi ft)}=1.\]Pro hodnotu maximálního indukovaného napětí tedy platí:
\[u_\mathrm{i_{max}}=\frac{\sqrt2\mu_0 f }{d} SI.\]Zápis a číselné dosazení
\(P=110\,\mathrm{W}\) příkon spotřebiče \(U=230\,\mathrm{V}\) efektivní hodnota napětí sítě \(f=50\,\mathrm{Hz}\) frekvence sítě \(S=2\,\mathrm{cm^2}=2{\cdot} 10^{-4}\,\mathrm{m^2}\) plocha smyčky \(d=10\,\mathrm{cm}=0{,}10\,\mathrm{m}\) vzdálenost smyčky od vodiče \(I=?\,\mathrm{(A)}\) efektivní hodnota elektrického proudu tekoucího přívodním vodičem \(B_\mathrm{max}=?\,\mathrm{(T)}\) maximální hodnota magnetické indukce v místě smyčky \(u_\mathrm{i_{max}}=?\,\mathrm{(V)}\) časový průběh magnetické indukce generované elektrickým proudem Z tabulek: \(\mu_0 =4 \pi\cdot 10^{-7}\,\mathrm{Hm^{-1}}\) permeabilita vakua
b)
\[I=\frac{P}{U}=\frac{110}{230}\,\mathrm{A}=0{,}48\,\mathrm{A}\]c)
\[B_\mathrm{max}=\frac{\sqrt2}{2}\frac{\mu_0 I}{\pi d} =\frac{\sqrt2}{2}\cdot\frac{4 \pi\cdot 10^{-7}\cdot 0{,}48}{\pi \cdot 0{,}1} \,\mathrm{T}\,\dot{=}\,1{,}4{\cdot}10^{-6}\,\mathrm{T}=1{,}4\,\mathrm{\mu T}\]d)
\[u_\mathrm{i_{max}}=\frac{\sqrt2\mu_0 f }{l} SI =\frac{\sqrt2{\cdot}4 \pi\cdot 10^{-7} \cdot 50 }{0{,}1}\cdot2{\cdot} 10^{-4}\cdot 0{,}48 \,\mathrm{V}\,\dot{=}\,8{,}5{\cdot} 10^{-8}\,\mathrm{V}\,\dot{=}\,85\,\mathrm{nV}\]Poznámka: Hodnota maximální magnetické indukce Bmax v závitu je velmi malá, dokonce menší než je hodnota magnetické indukce magnetického pole Země. Zemský magnetismus nemá vliv na indukované napětí, protože se cívka nehýbe a magnetická indukce magnetického pole Země je tedy konstantní (viz úloha Rotující cívka v magnetickém poli Země). Detekovat takto malá napětí vyžaduje velmi citlivý přístroj. Velikost magnetické indukce bychom mohli zvětšit např. tím, že místo jednoho závitu bychom použili plochou cívku.
Odpověď
Efektivní hodnota proudu má velikost 0,48 A.
Pro časový průběh magnetické indukce B(t) platí vztah \(B(t)=\frac{\sqrt2}{2}\frac{\mu I}{\pi d} \,\cos (\omega t).\)
Maximální hodnota magnetické indukce má přibližně velikost 1,4 μT.
Časový průběh indukovaného napětí ui(t) ve smyčce je popsán vztahem \(u_\mathrm{i}(t)=\frac{\sqrt2\mu f }{l} SI\,\sin ( 2\pi ft).\)
Maximální hodnota indukovaného napětí ve smyčce je roven přibližně hodnotě 85 nV.


