Elektrický dipól a bodový náboj
Úloha číslo: 237
Ideální dipól \(\vec p\) je ve vzdálenosti r od bodového náboje Q.
(a) Jaká síla působí na náboj Q?
(b) Jaká síla působí na dipól \(\vec p\)?
Část (b) řešte dvěma způsoby: podle zákona akce a reakce a přímým výpočtem pomocí vztahu pro sílu působící na dipól v elektrickém poli.
Nápověda – pole dipólu
Pro elektrickou intenzitu \(\vec E\) v místě určeném polohovým vektorem \(\vec r\) pole ideálního dipólu \(\vec p\) umístěného v počátku vztažné soustavy platí vztah
\[\vec{E} = \frac{1}{4\pi\varepsilon_0r^5}\left[3(\vec p\cdot\vec r)\vec r - r^2\vec p\right].\]Nápověda – síla působící na dipól v nehomogenním poli
V nehomogenním poli \(\vec E\) působí na dipól \(\vec p\) síla
\[\vec F = \nabla(\vec p \cdot \vec E) = (\vec p\cdot \nabla)\vec E.\]V homogenním poli je pravá strana zřejmě rovna nulovému vektoru.
Odvodit vztah pro sílu působící na dipól v nehomogenním poli lze takto: místo ideálního dipólu si představíme dipól neideální složený ze dvou bodových nábojů o velikosti +q, −q v malé vzdálenosti od sebe. Síly působící na oba náboje složíme a ve výsledném vztahu provedeme vhodnou aproximaci (limitní přechod k nulové vzdálenosti mezi náboji při zachování dipólového momentu).
Rozbor
Známe-li intenzitu elektrického pole \(\vec E\) v daném místě prostoru, umíme velmi jednoduše podle vztahu \(\vec F = Q\vec E\) vypočítat sílu, která v tomto místě působí na bodový náboj. Část (a) úlohy lze tedy vyřešit okamžitě. Známe-li ale sílu, kterou působí dipól na bodový náboj, pak podle zákona akce a reakce známe také sílu, kterou působí bodový náboj na dipól — bude stejně veliká a opačného směru.
Nechceme-li však použít třetího Newtonova zákona, nezbývá než v části (b) určit sílu, kterou působí bodový náboj na ideální dipól, přímým výpočtem.
Řešení části (a) — síla působící na bodový náboj
Vyřešíme nejprve část (a). Dipól umístíme do počátku vztažné soustavy, náboj do místa určeného polohovým vektorem \(\vec r\).
Pro elektrickou intenzitu \(\vec E\) pole ideálního dipólu \(\vec p\) umístěného v počátku vztažné soustavy v místě určeném polohovým vektorem \(\vec r\) platí vztah
\[\vec E = \frac{1}{4\pi\varepsilon_0r^5}\left[3(\vec p\cdot\vec r)\vec r - r^2\vec p\right].\]Odtud vyplývá, že na bodový náboj působí síla
\[\vec F = Q\vec E = \frac{Q}{4\pi\varepsilon_0r^5}\left[3(\vec p\cdot\vec r)\vec r - r^2\vec p\right].\]Podle zákona akce a reakce pak síla působící na dipól je stejně velká, má stejný směr a opačnou orientaci:
\[-\vec F = \frac{Q}{4\pi\varepsilon_0r^5}\left[-3(\vec p\cdot\vec r)\vec r + r^2\vec p\right].\]Řešení části (b) — síla působící na dipól
Nyní zvolme vztažnou soustavu tak, že bodový náboj Q se nachází v počátku a dipól v místě určeném polohovým vektorem \(\vec r\).
Sílu \(\vec F_\mathrm{d}\), kterou působí bodový náboj Q na dipól, spočteme přímo. Platí, že
\[\vec F_\mathrm{d} = (\vec p\cdot\nabla)\vec E,\]kde \(\vec E\) je intenzita elektrického pole v místě dipólu.
Jak k tomuto vztahu dojít, je popsáno v komentáři v závěru úlohy.
Nyní zbývá vypočítat pravou stranu rovnice. Protože elektrické pole vytváří bodový náboj, za elektrickou intenzitu \(\vec E\) dosadíme:
\[\vec E = \frac{Q}{4\pi\varepsilon_0}\frac{\vec r}{r^3},\]a proto platí pro x-ovou složku síly \(\vec F_\mathrm{d}\):
\[F_\mathrm{d_x} = (\vec p\cdot \nabla)E_\mathrm{x} = \left(p_\mathrm{x}\frac{\partial}{\partial x}+ p_\mathrm{y}\frac{\partial}{\partial y}+p_\mathrm{z}\frac{\partial}{\partial z}\right)\frac{Q}{4\pi\varepsilon_0}\frac{x}{(x^2+y^2+z^2)^{3/2}}.\]Vypočteme jednotlivé parciální derivace. Podle y:
\[\frac{\partial}{\partial y}\left(\frac{x}{(x^2+y^2+z^2)^{3/2}}\right) = \frac{-3}{2}\frac{x}{(x^2+y^2+z^2)^{5/2}}\cdot 2y = -\frac{3xy}{(x^2+y^2+z^2)^{5/2}},\]podle z:
\[\frac{\partial}{\partial z}\left(\frac{x}{(x^2+y^2+z^2)^{3/2}}\right) = \frac{-3}{2}\frac{x}{(x^2+y^2+z^2)^{5/2}}\cdot 2z = -\frac{3xz}{(x^2+y^2+z^2)^{5/2}}\]a podle x:
\[\frac{\partial}{\partial x}\left(\frac{x}{(x^2+y^2+z^2)^{3/2}}\right) = \frac{-3}{2}\frac{x}{(x^2+y^2+z^2)^{5/2}}\cdot 2x + \frac{1}{(x^2+y^2+z^2)^{3/2}} = \] \[=-\frac{3x^2}{(x^2+y^2+z^2)^{5/2}} + \frac{1}{(x^2+y^2+z^2)^{3/2}}.\]S přihlédnutím ke vztahu r2 = x2+y2+z2 tak dostáváme
\[\frac{\partial}{\partial y}\left(\frac{x}{(x^2+y^2+z^2)^{3/2}}\right) = -\frac{3xy}{r^5}\] \[\frac{\partial}{\partial z}\left(\frac{x}{(x^2+y^2+z^2)^{3/2}}\right) = -\frac{3xz}{r^5}\] \[\frac{\partial}{\partial x}\left(\frac{x}{(x^2+y^2+z^2)^{3/2}}\right) = -\frac{3x^2}{r^5} + \frac{1}{r^3}.\]Dosazením do vztahu pro x-ovou složku síly dostaneme po úpravách
\[F_\mathrm{d_x} = \frac{Q}{4\pi\varepsilon_0}\left[\frac{p_\mathrm{x}}{r^3}-\frac{3x}{r^5}(p_\mathrm{x}x+p_\mathrm{y}y+p_\mathrm{z}z)\right]= \frac{Q}{4\pi\varepsilon_0}\left[\frac{p_\mathrm{x}}{r^3}-\frac{3x}{r^5}(\vec p\cdot \vec r)\right],\]a to je vlastně x-ová složka vektoru:
\[= \frac{Q}{4\pi\varepsilon_0}\left[\frac{\vec p}{r^3}-\frac{3\vec r}{r^5}(\vec p\cdot \vec r)\right]_\mathrm{x}.\]Výpočet ostatních složek dopadne Vzhledem k symetrii v proměnných obdobně. Dostáváme, že
\[\vec F_\mathrm{d} = \frac{Q}{4\pi\varepsilon_0}\left[\frac{\vec p}{r^3}-\frac{3\vec r}{r^5}(\vec p\cdot \vec r)\right].\]To po jednoduchém vytknutí a úpravě dá totožný vztah jako v řešení části (a). Tedy až na znaménko — to je způsobeno použitím jiné vztažné soustavy, v níž má vektor \(\vec r\) opačnou orientaci než v části (a).
Výsledek
Na bodový náboj působí síla
\[\vec F = \frac{Q}{4\pi\varepsilon_0r^5}\left[3(\vec p\cdot\vec r)\vec r - r^2\vec p\right],\]kde \(\vec r\) je vektor s počátkem v místě dipólu a koncem v místě bodového náboje.
Na dipól pak působí síla
\[-\vec F = \frac{Q}{4\pi\varepsilon_0r^5}\left[-3(\vec p\cdot\vec r)\vec r + r^2\vec p\right].\]Komentář — odvození síly působící na dipól v elektrickém poli
Mějme dva bodové náboje +q, −q, stejně veliké a opačného znaménka, v místech \(\vec r_+,\ \vec r_-\) tvořící neideální dipól. Označme také
\[\vec d = \vec r_+ - \vec r_-\]vektor spojující záporný náboj s kladným.
Předpokládejme, že \(d\ll r_+\), \(d\ll r_-\). Dokážeme, že celkovou sílu, kterou působí elektrické pole na takový neideální dipól, můžeme aproximovat vztahem
\[\vec F = (\vec p\cdot \nabla)\vec E,\]kde \(\vec E\) je intenzita elektrického pole ve středu mezi oběma náboji.
Zřejmě celková síla je
\[\vec F = q(\vec E_+ - \vec E_-),\]kde \(\vec E_+,\ \vec E_-\) značí intenzitu pole v místech nábojů +q a −q. Podle níže uvedeného matematického odvození lze užít aproximaci
\[\vec E_+ - \vec E_- \approx (\vec d\cdot \nabla)\vec E,\]kde intenzitu \(\vec E\) bereme ve středu vektoru \(\vec d\). Odtud vyplývá hledaný vztah
\[\vec F = q(\vec E_+ - \vec E_-) \approx (q\vec d\cdot \nabla)\vec E = (\vec p\cdot \nabla)\vec E.\]Aproximace rozdílu dvou blízkých vektorů vyplývá z vektorové analýzy. Nastiňme jak. V následujících matematických úvahách symboly f, g a \(\vec F\) značí popořadě libovolnou funkci jedné proměnné f, libovolnou skalární funkci g a libovolnou vektorovou funkci \(\vec F\).
Jestliže máme funkci f jedné proměnné, pak její přírůstek můžeme aproximovat pomocí diferenciálu:
\[f(x+\Delta x)-f(x) \approx \Delta x\, \frac{{\rm d}f}{{\rm d}x}(x),\]přičemž tato aproximace je tím přesnější, čím je přírůstek Δx argumentu menší (a v limitě \(\Delta x\to 0\) nastává rovnost, je-li funkce diferencovatelná).
Máme-li nyní skalární funkci prostorových proměnných \(g(\vec r)\), potom malý přírůstek můžeme aproximovat podobným způsobem ve všech třech souřadnicích:
\[g(\vec r+\Delta\vec r)-g(\vec r) \approx \Delta x\,\frac{\partial g(\vec r)}{\partial x} + \Delta y\,\frac{\partial g(\vec r)}{\partial y} + \Delta z\,\frac{\partial g(\vec r)}{\partial z},\]kde značíme \(\Delta\vec r = (\Delta x,\, \Delta y,\, \Delta z)\). Pravou stranu můžeme také psát ve tvaru skalárního součinu
\[g(\vec r+\Delta\vec r)-g(\vec r) \approx \Delta\vec r\,\cdot\,\nabla g(\vec r).\]Aproximace je opět tím přesnější, čím je posunutí \(\Delta\vec r\) menší (a v limitě nastává rovnost).
Konečně pro vektorovou funkci \(\vec F(\vec r)\) aplikujeme předchozí vztah pro skalární funkci na každou její složku, to jest
\[F_\mathrm{x}(\vec r+\Delta\vec r)-F_\mathrm{x}(\vec r) \approx \Delta\vec r\,\cdot\,\nabla F_\mathrm{x}(\vec r)\] \[F_\mathrm{y}(\vec r+\Delta\vec r)-F_\mathrm{y}(\vec r) \approx \Delta\vec r\,\cdot\,\nabla F_\mathrm{y}(\vec r)\] \[F_\mathrm{z}(\vec r+\Delta\vec r)-F_\mathrm{z}(\vec r) \approx \Delta\vec r\,\cdot\,\nabla F_\mathrm{z}(\vec r),\]což lze zkráceně psát ve tvaru
\[\vec F(\vec r+\Delta\vec r)-\vec F(\vec r) \approx (\Delta\vec r\,\cdot\,\nabla)\vec F,\]kde operátor \((\Delta\vec r\,\cdot\,\nabla)\) působící na vektor je definován předpisem
\[\Delta\vec r\,\cdot\,\nabla = \Delta x\frac{\partial}{\partial x} + \Delta y\frac{\partial}{\partial y} + \Delta z\frac{\partial}{\partial z}. \]Při působení na vektor dává opět vektor, přičemž působí na každou složku. Pro složky vektoru \([(\Delta\vec r\,\cdot\,\nabla)\vec F]\) tedy při této konvenci dostáváme výsledek shodný s výše uvedenými vztahy:
\[[(\Delta\vec r\,\cdot\,\nabla)\vec F]_\mathrm{x} = \Delta x\frac{\partial F_\mathrm{x}}{\partial x} + \Delta y\frac{\partial F_\mathrm{x}}{\partial y} + \Delta z\frac{\partial F_\mathrm{x}}{\partial z} = \Delta\vec r \,\cdot\,\nabla F_\mathrm{x}\] \[[(\Delta\vec r\,\cdot\,\nabla)\vec F]_\mathrm{y} = \Delta x\frac{\partial F_\mathrm{y}}{\partial x} + \Delta y\frac{\partial F_\mathrm{y}}{\partial y} + \Delta z\frac{\partial F_\mathrm{y}}{\partial z} = \Delta\vec r \,\cdot\,\nabla F_\mathrm{y}\] \[[(\Delta\vec r\,\cdot\,\nabla)\vec F]_\mathrm{z} = \Delta x\frac{\partial F_\mathrm{z}}{\partial x} + \Delta y\frac{\partial F_\mathrm{z}}{\partial y} + \Delta z\frac{\partial F_\mathrm{z}}{\partial z} = \Delta\vec r \,\cdot\,\nabla F_\mathrm{z}.\]Komentář — speciální případy
Pro přiblížení výsledných vztahů spočteme sílu působící na dipól v některých speciálních případech. Připomeňme, že \(\vec r\) značí vektor mířící od bodového náboje Q k dipólu \(\vec p\).
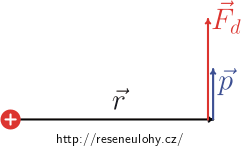
Vektor dipólového momentu \(\vec p\) je kolmý na vektor \(\vec r\). Potom
\[\vec p\,\cdot\,\vec r = 0\]a tedy
\[\vec F_\mathrm{d} = \frac{Q}{4\pi\varepsilon_0}\frac{\vec p}{r^3}.\]Síla tedy působí ve směru dipólového momentu, je-li náboj Q kladný, a ve směru opačném, je-li záporný.
Vektor dipólového momentu \(\vec p\) má stejný směr a stejnou orientaci jako vektor \(\vec r\). Potom
\[\vec p\,\cdot\,\vec r = pr, \qquad \frac{\vec p}{p} = \frac{\vec r}{r}\]a tedy
\[\vec F_\mathrm{d} = \frac{Q}{4\pi\varepsilon_0}\left[\frac{\vec p}{r^3}-\frac{3\vec r}{r^5}(\vec p\,\cdot\,\vec r)\right] = \frac{Q}{4\pi\varepsilon_0}\left[\frac{p\vec r}{r^4}-\frac{3p\vec r}{r^4}\right] = -\frac{Q}{2\pi\varepsilon_0}\frac{p\vec r}{r^4}.\]Síla se tedy snaží dipól ke kladnému náboji Q přitáhnout (a od záporného odpudit). To není překvapivé – z požadavku na směr a orientaci vektoru \(\vec p\) si můžeme dipól představit jako dvojici nábojů opačného znaménka, z nichž záporný je bodovému náboji Q o něco blíže než ten kladný.
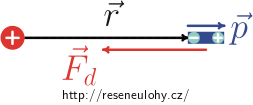
Vektor dipólového momentu \(\vec p\) má stejný směr a opačnou orientaci než vektor \(\vec r\). Potom
\[\vec p\,\cdot\,\vec r = -pr, \qquad \frac{\vec p}{p} = -\frac{\vec r}{r}\]a tedy
\[\vec F_\mathrm{d} = \frac{Q}{4\pi\varepsilon_0}\left[\frac{\vec p}{r^3}-\frac{3\vec r}{r^5}(\vec p\,\cdot\,\vec r)\right] = \frac{Q}{4\pi\varepsilon_0}\left[-\frac{p\vec r}{r^4}+\frac{3p\vec r}{r^4}\right] = \frac{Q}{2\pi\varepsilon_0}\frac{p\vec r}{r^4}\]síla se tedy snaží dipól od kladného náboje Q odpudit (a k zápornému přitáhnout). To si opět můžeme lehko vysvětlit na představě neideálního dipólu — z požadavku na směr a orientaci vektoru \(\vec p\) si můžeme dipól představit jako dvojici nábojů opačného znaménka, z nichž kladný je bodovému náboji Q o něco blíže než ten záporný.


