Sbírka řešených úloh

Válec s dutinou

Úloha číslo: 2309

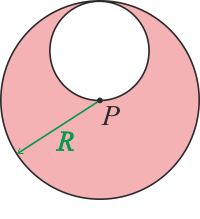
Dlouhá měděná tyč s poloměrem R má mimo svou osu válcovou dutinu podél celé své délky tak, jak je znázorněno na obrázku. Vodičem protéká proud I, který směřuje ven z obrázku, a je rovnoměrně rozložený v celém řezu vodiče.

Nalezněte velikost a směr magnetického pole uprostřed tyče, tj. v bodě P.

• Nápověda – princip superpozice

  Napadá vás nějaký elegantní způsob, jak se „vypořádat“ s dutinou ve vodiči, když není umístěna symetricky?

• Řešení nápovědy − princip superpozice

  S dutinou se „vypořádáme“ principem superpozice. Vodič s dutinou si představíme jako vodič bez dutiny + vodič s proudem mířícím na druhou stranu (umístěný namísto dutiny). Spočítáme magnetické pole od válcového vodiče bez dutiny. Poté odečteme magnetické pole, které by vytvořil válcový vodič umístěný namísto dutiny a jímž by tekl proud opačným směrem.

  Takový postup můžeme aplikovat, protože válcový vodič s dutinou je vlastně plný vodič bez dutiny a tenčí plný vodič (na místě dutiny), kterým teče proud opačným směrem.

• Nápověda − magnetické pole tlustého vodiče

  V této úloze využijeme poznatků z úlohy Tlustý přímý vodič o poloměru R.

  Jaké konkrétní vztahy by se mohly v této úloze použít?

• Řešení nápovědy − magnetické pole tlustého vodiče

  Vztah pro velikost magnetické indukce uvnitř tlustého přímého vodiče je

  \[B=\frac{\mu_0 }{2\pi}\frac{I}{R^2} r=\frac{\mu_0}{2\pi}\frac{jS}{R^2}r=\frac{\mu_0}{2\pi}\frac{j\pi R^2}{R^2}r=\frac{\mu_0}{2}j r,\]

  kde \(R\) je poloměr vodiče, r < R je vzdálenost místa, ve kterém počítáme magnetickou indukci od středu vodiče, \(j\) je proudová hustota a \(S\) je obsah kružnice o poloměru \(r\).

  Ve speciálním případě, kdy počítáme magnetickou indukci přesně uprostřed tlustého vodiče (\(r=0\)), je magnetická indukce nulová. Pro magnetické pole na povrchu tlustého vodiče platí, že je rovno magnetickému poli, které by vytvořil dlouhý přímý vodič, jímž by procházel stejný proud. Dosaďme do vztahu \(r=R\) a \(I=jS\) a upravme:

  \[B=\frac{\mu_0}{2}j r=\frac{\mu_0}{2}jR=\frac{\mu_0}{2}\frac{ IR}{S}=\frac{\mu_0}{2}\frac{IR}{\pi R^2}=\frac{\mu_0}{2\pi}\frac{ I}{R}.\]

• Řešení

  Pro určení magnetického pole v bodě P využijeme princip superpozice neboli principu, že válcový vodič s dutinou odpovídá plnému vodiči a tenčímu vodiči (na místě dutiny), kterým teče proud opačným směrem.

  

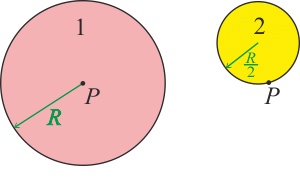
  Pro magnetické pole v bodě P válcového vodiče s dutinou platí

  \[\vec{B}=\vec{B}_1+\vec{B}_2,\tag{1}\]

  kde \(\vec{B}_1\) je magnetické pole v bodě P od válcového vodiče 1 a \(\vec{B}_2\) je magnetické pole v bodě P od válcového vodiče 2. Připomeňme, že proud v prvním vodiči teče z obrázku ven a proud v druhém vodiči teče do obrázku.

  Abychom mohli vyjádřit \(B_1\) a \(B_2\), potřebujeme vyjádřit plošnou proudovou hustotu j.

  

  Válcovým vodičem prochází rovnoměrně rozložený celkový proud I. Zřejmě platí

  \[I=S j,\]

  kde \(S\) je obsah průřezu válcového vodiče. Postupnými úpravami získáme

  \[j=\frac{I}{S}=\frac{I}{\pi R^2-\pi\left(\frac{R}{2}\right)^2}=\frac{I}{\pi\frac{3R^2}{4}}=\frac{4I}{3\pi R^2}.\]

  Spojením posledního vztahu a vzorce z řešení nápovědy (magnetické pole tlustého vodiče) získáme vztah popisující velikost magnetického pole uvnitř tlustého přímého vodiče s proudem I v bodě vzdáleném r < R od středu tohoto vodiče.

  \[B=\frac{\mu_0}{2}r\frac{4I}{3\pi R^2}=\frac{2\mu_0}{3\pi}\frac{I r}{R^2}.\tag{2}\]

  Využijme vztahu (2) a vyjádřeme \(B_1\) a \(B_2\).

  Jelikož je bod \(P\) ve středu (\(r=0\)) růžového vodiče, vyjádříme velikost \(B_1\) jako

  \[B_1=\frac{2\mu_0}{3\pi}\frac{I r}{R^2}=0 \space \mathrm{T}.\]

  Uvědomme si, že jsme k tomuto výsledku mohli dojít i úvahou. Jelikož počítáme magnetické pole ve středu tlustého vodiče, kolem kterého je proud rozložen symetricky, jednotlivé příspěvky se vzájemně vyruší a magnetická indukce vyjde nulová (výpočet i viz nápověda).

  Bod \(P\) je na kraji (\(r=\frac{R}{2}\)) žlutého vodiče, tudíž vyjádříme velikost \(B_2\) jako

  \[B_2=\frac{2\mu_0}{3\pi}\frac{I \left(\frac{R}{2}\right)}{R^2}=\frac{\mu_0}{3\pi}\frac{I }{R}.\]

  Příspěvek \(\vec{B}_2\) je magnetické pole v bodě \(P\) na okraji žlutého vodiče. Proud teče do obrázku. Směr magnetického pole určíme pomocí Ampérova pravidla pravé ruky.

  

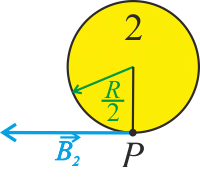
  Vrátíme-li se ke vztahu (1) a dosadíme-li vypočtené magnetické indukce, vyjde nám

  \[\vec{B}=\vec{B}_1+\vec{B}_2=\vec{B}_2.\]

  Neboli výsledné magnetické pole v bodě \(P\) odpovídá magnetickému poli \(\vec{B}_2.\) Tudíž velikost magnetického pole v bodě \(P\) je

  \[B=\frac{\mu_0}{3\pi}\frac{I }{R}\]

  a směr ukazuje následující obrázek.

  

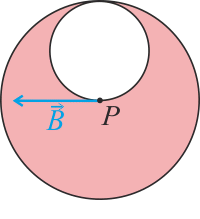
  Pozn.: Uvědomme si, že tímto způsobem (použitím principu superpozice) můžeme určit magnetickou indukci v libovolném bodě uvnitř či vně „děravého“ vodiče.

• Odpověď

  Magnetické pole v bodě P má velikost

  \[B=\frac{\mu_0 I}{3\pi R},\]

  směr ukazuje následující obrázek.