Vodivá smyčka v proměnném magnetickém poli
Úloha číslo: 357
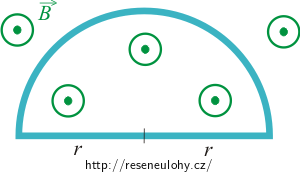
Půlkruhová vodivá smyčka o poloměru 20 cm a elektrickém odporu 2 Ω se nachází v homogenním magnetickém poli. Vektor magnetické indukce je kolmý na rovinu smyčky a jeho velikost se mění s časem t podle vztahu B = (4t2+2t+3) T, kde je zapotřebí čas dosadit v sekundách. Určete:
a) vztah pro okamžité napětí indukované v této smyčce v závislosti na čase t a velikost indukovaného napětí ve smyčce v čase 2 s,
b) velikost a směr proudu smyčkou v čase 2 s,
c) teplo uvolněné v časovém intervalu 0 s až 2 s.
Nápověda a) Indukované napětí
Ve smyčce se indukuje napětí, pokud se mění magnetický indukční tok smyčkou. Tuto závislost popisuje Faradayův zákon elektromagnetické indukce, jehož matematicky zápis má tvar:
\[u_\mathrm{i}=-\frac{\,\mathrm{d}\Phi}{\,\mathrm{d}t}.\]Nápověda b) Velikost a směr indukovaného elektrického proudu
Velikost elektrického proudu určíme z Ohmova zákona.
Směr indukovaného proudu ve smyčce je dán Lenzovým zákonem a Ampérovým pravidlem pravé ruky.
Lenzův zákon
Indukovaný proud ve smyčce má takový směr, že magnetické pole vytvořené tímto proudem působí proti změně magnetického pole, která ho vyvolala.
Ampérovo pravidlo pravé ruky
Naznačíme-li uchopení vodiče do pravé ruky tak, aby palec ukazoval dohodnutý směr proudu ve vodiči, pak prsty ukazují orientaci magnetických indukčních čar.
Nápověda c) Joulovo teplo
Zákon zachování energie nám říká, že pokles jedné formy energie se projeví růstem jiné formy energie.
V našem případě se elektrická potenciální energie potřebná k přenesení náboje mezi dvěma body o různém potenciálu přemění na teplo (tzv. Joulovo teplo), tj. na vnitřní energii.
Rozbor
Vztah pro okamžité napětí
Indukované elektromagnetické napětí ve smyčce vzniká díky elektromagnetické indukci a závisí na časové změně celkového magnetického toku uzavřenou smyčkou. Matematicky popisuje tuto závislost tzv. Faradayův zákon elektromagnetické indukce.
Magnetický indukční tok plochou si můžeme představit jako „tok“ magnetických indukčních čar danou plochou. Magnetický tok plochou je tedy úměrný počtu indukčních čar procházejících plochou.
Velikost a směr elektrického proudu procházejícího smyčkou
Velikost indukovaného proudu určíme pomocí Ohmova zákona, kde za napětí dosadíme indukované elektromagnetické napětí v daném okamžiku.
Směr indukovaného proudu ve smyčce bude takový, aby magnetické pole vytvořené tímto proudem bylo namířeno proti změně, která indukovaný proud vyvolala, tzv. Lenzův zákon.
Uvolněné teplo
Při přenesení náboje ve smyčce mezi dvěma místy vykoná indukované elektrické pole práci, která se rovná změně elektrické potenciální energie daného náboje. Zákon zachování energie nám říká, že pokles elektrické potenciální energie se projeví růstem jiné formy energie.
V našem případě si smyčku můžeme představit jako rezistor a jeden závit ideální cívky. S růstem proudu tedy poroste energie magnetického pole v cívce a v rezistoru se energie bude přeměňovat na (tzv. Joulovo) teplo, tj. na vnitřní energii.
Řešení a) Indukované napětí
Vztah pro okamžité napětí
Elektromagnetické napětí ui(t) ve smyčce vzniká při časové změně magnetického toku smyčkou. Matematický zápis tohoto vztahu je označován jako Faradayův zákon elektromagnetické indukce a zní:
\[u_\mathrm{i}(t)=-\frac{\,\mathrm{d}\Phi}{\,\mathrm{d}t}.\tag{1}\]Magnetický tok Φ uzavřenou plochou S je dán integrálem přes plochu uvnitř smyčky S:
\[\Phi=\int_\mathrm{S}{\vec{B}\cdot\,\mathrm{d}\vec{S}}.\]Jelikož v našem případě je vektor magnetické indukce kolmý na plochu smyčky, můžeme integrál psát ve tvaru:
\[\Phi=\int{B}\,\mathrm{d}S.\]Díky tomu, že velikost magnetické indukce je (v daném čase) konstantní na celé ploše smyčky, můžeme integrál spočítat:
\[\Phi=\int{B}\,\mathrm{d}S={B}\int\,\mathrm{d}S=BS.\tag{2}\]V našem příkladě se velikost magnetické indukce B mění s časem podle vztahu:
\[B(t)=\left(4t^2+2t+3\right)\,\mathrm{T}\]a plocha smyčky S je rovna obsahu půlkružnice o poloměru r:
\[S=\frac{\pi r^2}{2}.\]Velikost magnetické indukce a obsah plochy smyčky dosadíme do rovnice (2) pro výpočet magnetického toku smyčkou:
\[\Phi=BS=\frac{\pi r^2}{2}\left(4t^2+2t+3\right).\]Výraz pro magnetický indukční tok dosadíme do rovnice (1) pro velikost indukovaného elektromagnetického napětí ui(t):
\[u_\mathrm{i}(t)=-\frac{\,\mathrm{d}\Phi}{\,\mathrm{d}t},\] \[u_\mathrm{i}(t)=-\frac{\pi r^2}{2}\frac{\,\mathrm{d}\left(4t^2+2t+3\right)}{\,\mathrm{d}t}.\]Po zderivování podle času dostáváme vztah pro okamžité napětí ui(t) indukované v půlkruhové smyčce v čase t:
\[u_\mathrm{i}(t)=-\frac{\pi r^2}{2}\left(8t+2\right)\,\mathrm{T}.\]Poznámka: Jak je uvedeno v zadání, čas do všech vztahů v této úloze dosazujeme v sekundách, vzdálenost dosadíme v metrech a hledané napětí dostaneme ve voltech.
Velikost indukovaného napětí
Velikost indukovaného napětí se rovná absolutní hodnotě indukovaného elektromagnetického napětí. To znamená, že do vztahu pro okamžitou hodnotu indukovaného napětí dosadíme konkrétní časový údaj t = 2 s a poloměr smyčky r = 20 cm = 0,20 m:
\[|u_\mathrm{i}(1)|=\frac{\pi\cdot 0{,}20^2}{2}\left(8{\cdot}2+2\right)\,\mathrm{V}\,\dot{=}\,1{,}1\,\mathrm{V}.\]Řešení b) Velikost a směr indukovaného proudu smyčkou
Velikost indukovaného proudu
Velikost indukovaného proudu I určíme pomocí Ohmova zákona:
\[U=R\cdot I,\]kde za napětí U dosadíme indukované elektromagnetické napětí ui(t).
Pro elektrický proud tedy získáme vztah:
\[I=\frac{|u_\mathrm{i}(t)|}{R}.\]Po dosazení konkrétních hodnotn pro indukované napětí ui(t = 2 s) a odporu R = 2 Ω dostáváme:
\[I=\frac{1{,}1}{2}\,\mathrm{A}\dot{=}0{,}6\,\mathrm{A}.\]Elektrický proud, který se indukuje ve smyčce v čase 2 s, má přibližně velikost I = 0,6 A.
Směr indukovaného proudu
Směr indukovaného proudu ve smyčce je dán Lenzovým zákonem (viz nápověda).
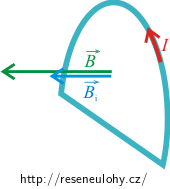
Použití zákona ukážeme na obrázku, na kterém je znázorněna nehybná vodivá smyčka umístněná v magnetickém poli, jehož magnetická indukce \(\vec{B}\) s časem roste.
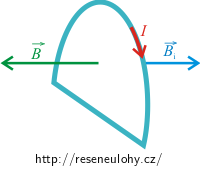
Tím dochází ke změně magnetického toku, ve smyčce se indukuje elektromagnetické napětí a obvodem smyčky protéká indukovaný proud (viz předchozí oddíl).
Indukovaný proud vytváří v okolí smyčky magnetické pole o indukci \(\vec{B}_\mathrm{i}\). Vektory \(\vec{B}_\mathrm{i}\) a \(\vec{B}\) jsou podle Lenzova pravidla opačně orientované, aby magnetické pole indukovaného proudu působilo proti nárůstu velikosti magnetické indukce, který byl příčinou vzniku indukovaného proudu.
Směr proudu určíme pomocí Ampérova pravidla pravé ruky (viz nápověda).
V našem případě bude smyčkou procházet elektrický proud ve směru hodinových ručiček.
Řešení c) Výpočet tepla
Při přenesení náboje mezi dvěma místy vykoná elektrické pole práci, která se rovná změně potenciální energie. Zákon zachování energie nám říká, že pokles elektrické potenciální energie způsobí nárůst jiné formy energie, v našem případě se část energie přemění na teplo (tzv. Joulovo teplo).
Pro Joulovo teplo uvolněné za daný čas platí:
\[Q=\int_{0}^{t} P(t)\,\mathrm{d}t.\tag{3}\]Smyčka se chová jako jeden závit reálné cívky, kterou si můžeme představit jako rezistor a ideální cívku. Energie se bude přeměňovat na Joulovo teplo v rezistoru. Pro výkon P elektrického proudu na rezistoru obecně platí:
\[P=\frac{U^2}{R}.\]V našem případě dosadíme za napětí U časově proměnné indukované napětí ui. Po dosazení do rovnice (3) pro výpočet tepla dostáváme vztah:
\[Q=\int_{0}^{t}\frac{{{u_\mathrm{i}}(t)}^2}{R}\,\mathrm{d}t.\]Indukované napětí ui(t) závisí na čase t podle vztahu:
\[u_\mathrm{i}(t)=-\frac{\pi r^2}{2}\left(8t+2\right).\]Vztah pro indukované napětí dosadíme do výrazu pro teplo Q:
\[Q=\int_{0}^{t}\frac{\left(-\frac{\pi r^2}{2}\left(8t+2\right)\right)^2}{R}\,\mathrm{d}t.\]Časový interval, ve kterém určujeme Joulovo teplo, je \(t\in\langle0{,}2\rangle\,\mathrm{s}\):
\[Q=\int_{0}^{2}\frac{\left(\frac{\pi r^2}{2}\left(8t+2\right)\right)^2}{R}\,\mathrm{d}t.\]Výraz umocníme a výrazy, které nezávisí na čase, vytkneme před integrál:
\[Q=\frac{\pi^2 r^4}{4R}\int_{0}^{2} (64t^2+32t+4)\,\mathrm{d}t.\]Rovnici integrujeme podle času:
\[Q=\frac{\pi^2 r^4}{4R}\,\left[\frac{64t^3}{3}+\frac{32t^2}{2}+4t\right]_0^2.\]Dosadíme meze:
\[Q=\frac{\pi^2 r^4}{4R}\,\left[\frac{64{\cdot}2^3}{3}+\frac{32{\cdot}2^2}{2}+4{\cdot}2-0\right]=\frac{\pi^2 r^4}{4R}\,\left[\frac{512}{3}+64+8\right]=\frac{\pi^2 r^4}{R}\cdot \frac{182}{3}.\]Po dosazení konkrétních hodnot poloměru smyčky r = 0,2 m a odporu R = 2 Ω dostáváme pro velikost tepla:
\[Q=\frac{\pi^2 0{,}2^4}{2}\cdot \frac{182}{3}\,\mathrm{J}\,\dot{=}\,0{,}48\,\mathrm{J}.\]Odpověď
Pro okamžité napětí indukované ve vodivé smyčce platí vztah \(u_\mathrm{i}(t)=-\frac{\pi r^2}{2}\left(8t+2\right)\,\mathrm{V},\) do kterého čas dosazujeme v sekundách a poloměr v metrech.
Velikost indukovaného napětí v čase 2 s má velikost přibližně 1,1 V.
Smyčkou prochází v čase 2 s indukovaný elektrický proud o velikosti 0,6 A. Indukovaný elektrický proud ve smyčce proudí ve směru hodinových ručiček.
Během prvních 2 sekund se na smyčce uvolní teplo 0,48 J.