Válec na nakloněné rovině
Úloha číslo: 480
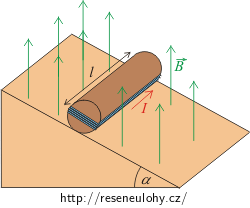
Válec o hmotnosti 250 g a délce 10 cm, kolem něhož je v podélném směru hustě navinuto 10 závitů vodiče, se nachází na nakloněné rovině s úhlem náklonu 30°. Určete minimální proud protékající cívkou, který zabrání válci ve valivém pohybu po nakloněné rovině, jestliže se válec nachází v magnetickém poli o indukci 0,5 T, které je orientované svisle vzhůru.
Nápověda
Nakreslete si všechny síly působící na válec s cívkou a určete, jaké směry budou mít jejich silové momenty.
Rozbor
Na válec s cívkou na nakloněné rovině působí tíhová síla, která způsobí valení válce směrem dolů. Osa rotace tohoto pohybu je na styku podložky s válcem. Působení tíhové síly můžeme charakterizovat silovým momentem.
Díky tomu, že cívkou, která je namotaná na válec, prochází proud ve vhodně zvoleném směru a cívka se nachází v magnetickém poli, působí na její strany magnetické síly, jejichž směr určíme pomocí Flemingova pravidla levé ruky.
Magnetické síly působící na strany cívky působí na válec také momentem sil.
Aby se válec nevalil po nakloněné rovině, ale setrval v klidu na jednom místě, musí být vektorový součet momentů všech sil vzhledem k ose otáčení nulový vektor.
Směr proudu ve vodiči a celkové geometrické uspořádání musí být takové, aby magnetické síly působící na stranu cívky měly takový směr, že silový moment vyvolaný těmito silami bude mít opačný směr oproti silovému momentu vyvolanému tíhovou silou. A aby byl vektorový součet obou momentů nulový, musí se rovnat velikosti obou momentů.
Řešení
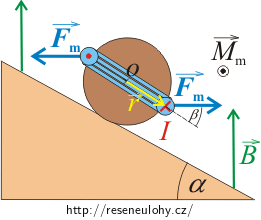
Tíhová síla \(\vec{F}_\mathrm{G}\) způsobí valení válce po nakloněné rovině směrem dolů. Pro silový moment \(\vec{M}\) této síly platí
\[\vec{M}=\vec{r}\times \vec{F}_\mathrm{G},\]kde \(\vec{r}\) je rameno otáčení, jehož velikost je rovna poloměru podstavy válce.
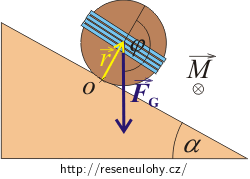
Směr momentu otáčení je určen pravidlem pravé ruky a směřuje za obrázek.
Pro velikost silového momentu M platí
\[M=rF_\mathrm{G} \sin{\varphi},\]kde úhel φ je úhel mezi vektory \(\vec{r}\) a \(\vec{F}_\mathrm{G}\), jehož hodnota sin φ odpovídá sin α, tedy
\[\sin{\varphi}=\sin{\alpha},\]kde úhel α je úhel náklonu roviny. Tato rovnost může nastat, protože úhel náklonu roviny α odpovídá doplňkovému úhlu do 180° k úhlu φ.
Osou otáčen9 je místo styku podložky s válcem (viz obrázek).
Za velikost tíhové síly dosadíme
\[F_\mathrm{G}=mg.\]Pro velikost silového momentu M vyvolaného tíhovou silou tak dostáváme výraz
\[M=rmg\,\sin{\alpha}.\]Aby se válec nevalil po nakloněné rovině, ale setrval v klidu na jednom místě, musí na něj působit síla, jejíž moment bude mít stejnou velikost, ale opačný směr oproti mechanickému momentu tíhové síly, tedy
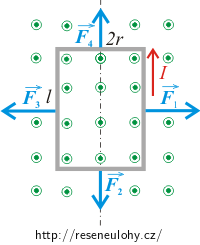
\[M=M_\mathrm{m}.\]Pro vyjádření velikosti momentu Mm magnetické síly \(\vec{F}_\mathrm{m}\) vyšetříme síly, které působí na jednotlivé strany obdélníkové cívky umístěné v magnetickém poli.
Velikosti sil působící na jednotlivé strany obdélníkové smyčky určíme pomocí vztahu
\[F_\mathrm{m}=I|\vec{l}\times\vec{B}|=IlB\,\sin{\varphi},\]kde úhel φ je úhel mezi vektorem magnetické indukce \(\vec{B}\) a směrem proudu.
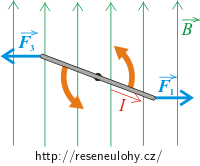
Magnetické síly působící na strany cívky rovnoběžné s obrázkem
Na strany cívky rovnoběžné s obrázkem působí síly o stejné velikosti, ale opačném směru. Tyto síly se tedy vyruší, jejich výslednice je nulová. Protože spojnice jejich působišť leží v ose smyčky, bude jejich výsledný moment rovněž nulový. Síly rovnoběžné s obrázkem tedy nepřispívají k otáčení cívky.
Magnetické síly působící na strany cívky kolmé k obrázku
Velikost sil působících na strany cívky kolmé k obrázku mají také stejnou velikost a opačný směr, takže nemohou uvést smyčku do posuvného pohybu. Neleží ale na společné přímce, takže vytvářejí nenulový výsledný moment sil. Jedná se o tzv. dvojici sil, moment dvojice sil je nezávislý na volbě osy otáčení.
Poznámka: Podrobnější popis a obrázky jsou uvedeny v řešení nápovědy.
Směr proudu, který prochází částí cívky kolmé k obrázku, svírá se směrem vektoru magnetické indukce pravý úhel, tj. φ = 90°. Pro velikost magnetické síly působící na vodič délky l platí
\[F_1=F_2=BIl\,\sin{90^{\circ}}=BIl.\]Protože má cívka N závitů, výsledná síla, která působí na jednu stranu cívky, má velikost
\[F_\mathrm{m}=NBlI.\]Velikost ani směr této síly se při otáčení válce nemění.
Momenty obou magnetických sil mají stejný směr před obrázek, jsou kolmé k rovině určené oběma silami a celkový moment má velikost
\[M_\mathrm{m}=2rF_\mathrm{m}\,\sin{\beta},\]kde úhel β představuje úhel mezi vektorem \(\vec{r}\) a magnetickou silou \(\vec{F}_\mathrm{m}\). Tento úhel se mění při otáčení válce. Maximální hodnota pro sin β nastane pro svislou polohu cívky, tzn. β = 90° a sin β = 1. Při této poloze cívky bude hodnota momentu působícího na cívku maximální. Z ní pak vyjádříme minimální proud, který musí cívkou procházet.
Po dosazení za velikost magnetické síly Fm dostáváme pro velikost maximálního silového momentu Mmax
\[M_\mathrm{max}=2rBlIN.\]Aby se válec nevalil po nakloněné rovině, musí se velikosti momentů tíhové i magnetických sil rovnat
\[M=M_\mathrm{max},\] \[rmg\,\sin{\alpha}=2rBlIN.\]Odtud vyjádříme neznámý proud I:
\[I= \frac{mg\,\sin{\alpha}}{2BlIN}.\]Jedná se o minimální proud, který musí cívkou protékat, aby se při vhodné poloze nezačala valit dolů po nakloněné rovině.
Zápis a číselné dosazení
\(m=250\,\mathrm{g}=0{,}25\,\mathrm{kg}\) hmotnost válce \(l=10\,\mathrm{cm}=0{,}10\,\mathrm{m}\) délka válce \(N=10\) počet závitů vodiče \(B=0{,}50\,\mathrm{T}\) velikost indukce mg. pole \(\alpha=30^{\circ}\) náklon roviny \(I=?\,\mathrm{(A)}\) minimální proud protékající cívkou, který zabrání válci ve valivém pohybu po nakloněné rovině Z tabulek: \(g=9{,}81\,\mathrm{m\,s^{-2}}\) tíhové zrychlení
\[I= \frac{mg\,\sin{\alpha}}{2BlN}=\frac{0{,}25{\cdot} 9{,}81\cdot \sin{30^{\circ}}}{2{\cdot} 0{,}50{\cdot} 0{,}10{\cdot} 10}\,\mathrm{A}\,\dot{=}\,1{,}2\,\mathrm{A}\]Odpověď
Aby se válec s cívkou nepohyboval po nakloněné rovině dolů, ale setrval v klidu, musí cívkou procházet minimálně proud o velikosti přibližně 1,2 A (pokud v počáteční poloze cívka navinutá na válci leží ve svislé rovině). Pokud by cívkou procházel proud o větší velikosti, válec by se při vhodné poloze začal pohybovat směrem nahoru.