Sbírka řešených úloh

Nulová magnetická indukce mezi přímými vodiči s proudy

Úloha číslo: 471

Mějme dva nekonečné rovnoběžné vodiče, kterými prochází proudy 1 A a 2 A stejným směrem. Vodiče jsou ve vzdálenosti 6 cm. Určete geometrické místo všech bodů, ve kterých je celková magnetická indukce nulová.

• Nápověda

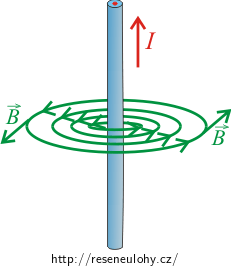
  Nakreslete si obrázek magnetického pole, které ve svém okolí vytváří přímý vodič s proudem.

  Výsledný vektor magnetické indukce mezi vodiči bude nulový, pokud budou mít v daném bodě vektory jednotlivých magnetických indukcí stejnou velikost a opačný směr.

• Řešení nápovědy – Magnetické pole přímého vodiče s proudem

  V okolí vodiče, kterým prochází elektrický proud, se vytváří magnetické pole charakterizované magnetickou indukcí. Indukční čáry vektoru magnetické indukce \(\vec{B}\) mají tvar soustředných kružnic se středem ve vodiči.

  

  Směr vektoru magnetické indukce \(\vec{B}\) určíme pomocí Ampérova pravidla pravé ruky a to tak, že položíme palec pravé ruky ve směru proudu ve vodiči a zahnuté prsty ukazují směr magnetických indukčních čar.

  Pro velikost vektoru magnetické indukce B od dlouhého přímého vodiče s proudem platí vztah

  \[B= \frac{\mu_\mathrm{0}}{2\pi}\,\frac{I}{R},\]

  kde I je proud procházející vodičem a R je kolmá vzdálenost od vodiče, ve které určujeme velikost magnetické indukce.

  Vztah je zde uveden bez odvození, protože jej nelze odvodit prostředky středoškolské matematiky. Podrobné odvození pomocí vysokoškolské matematiky naleznete v úloze Magnetické pole dlouhého přímého vodiče s proudem.

• Rozbor

  V okolí vodiče, kterým prochází elektrický proud, se vytváří magnetické pole charakterizované magnetickými indukčními čarami. Tyto magnetické indukční čáry mají tvar soustředných kružnic se středem ve vodiči. Vektor magnetické indukce v libovolném bodě mimo vodič je určen tečnou na příslušnou indukční čáru a jeho směr je dán Ampérovým pravidlem pravé ruky.

  Celková magnetická indukce je dána součtem vektorů magnetických indukcí obou vodičů. Jestliže si uvědomíme, jak se sčítají vektory, zjistíme, že v místě nulové celkové magnetické indukce musí oba vektory mít opačný směr a stejnou velikost, čímž se „odečtou“.

  

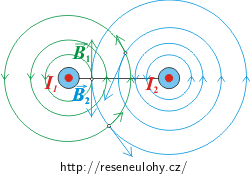
  Pokud si nakreslíme magnetické indukční čáry od obou vodičů, zjistíme, že opačný směr mají vektory magnetických indukcí od jednotlivých vodičů v prostoru mezi vodiči, tj. na části roviny spojující oba vodiče. Zbývá určit místo, kde mají oba vektory stejnou velikost.

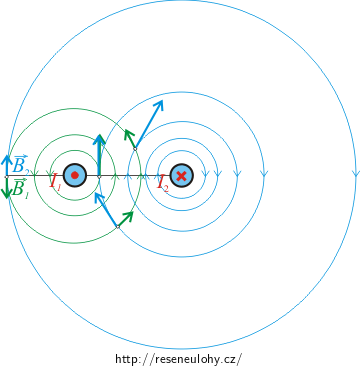
  Poznámka: Pokud by vodiči procházely proudy v různých směrech, vektory magnetických indukcí od obou vodičů by měly mezi vodiči stejný směr a výsledné pole mezi vodiči by bylo větší oproti tomu, kdyby zde byl přítomný pouze jeden vodič. Opačný směr by oba vektory magnetické indukce měly v místech roviny obou vodičů, které leží mimo prostor mezi vodiči.

  

• Řešení

  Magnetická pole kolem vodičů s proudem jsou charakterizovaná pomocí magnetických indukčních čar, jejichž směr je dán pravidlem pravé ruky (viz obrázek).

  

  Protože vodiči prochází stejně orientované proudy, mají vektory magnetických indukcí \(\vec{B_1}\) a \(\vec{B_2}\) od obou vodičů opačný směr na bodech mezi vodiči (na rovině spojující oba vodiče). Pokud chceme najít místo mezi vodiči, kde je výsledná magnetická indukce nulová, musíme najít bod, ve kterém se velikosti vektorů magnetických indukcí od jednotlivých vodičů rovnají. To znamená:

  \[B_1=B_2.\]

  Za velikosti vektorů magnetických indukcí dosadíme vztah pro velikost vektoru magnetické indukce dlouhého přímého vodiče s proudem (viz nápověda)

  \[B=\frac{\mu_\mathrm{0}}{2\pi}\,\frac{I}{R},\]

  kde I je velikost proudu procházejícím ve vodiči a R je vzdálenost bodu, ve kterém určujeme velikost vektoru magnetické indukce \(\vec{B}\) od vodiče.

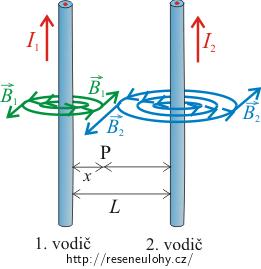
  Označme vzdálenost tohoto bodu od prvního vodiče x. Vztah pro velikost vektoru magnetické indukce B₁ od prvního vodiče pak bude mít tvar

  \[B_1=\frac{\mu_\mathrm{0}}{2\pi}\,\frac{I_1}{x},\]

  kde I₁ je proud procházející prvním vodičem. Pro velikost vektoru magnetické indukce B₂ od druhého vodiče bude platit

  \[B_2=\frac{\mu_\mathrm{0}}{2\pi}\,\frac{I_2}{(L-x)},\]

  kde I₂ je proud procházející druhým vodičem a (L − x) je vzdálenost hledaného bodu od druhého vodiče.

  Výrazy pro velikosti jednotlivých magnetických indukcí porovnáme:

  \[B_1=B_2,\] \[\frac{\mu_\mathrm{0}I_1}{2\pi x}=\frac{\mu_\mathrm{0}I_2}{2\pi(L-x)}\]

  a vyjádříme neznámou vzdálenost x. Nejprve zkrátíme stejné výrazy:

  \[\frac{I_1}{x}=\frac{I_2}{(L-x)}\]

  a „zbavíme“ se zlomků:

  \[(L-x) I_1=x I_2,\] \[LI_1-xI_1=x I_2.\]

  Výrazy s neznámou x převedeme na jednu stranu a vytkneme x:

  \[x(I_1+I_2)=LI_1.\]

  Z výrazu vyjádříme neznámou x

  \[x=\frac{LI_1}{(I_1+I_2)}.\]

  Získali jsme vztah pro vzdálenost bodu od prvního vodiče, ve kterém je velikost magnetické indukce nulová.

  Poznámka: Velikost magnetické indukce není nulová pouze v jednom bodě P mezi vodiči, ale ve všech bodech přímky, která leží v rovině vodičů a prochází bodem P.

• Zápis a číselné dosazení

  \(I_1\,=\,1\,\mathrm{A}\)	proud tekoucí prvním vodičem
  \(I_2\,=\,2\,\mathrm{A}\)	proud tekoucí druhým vodičem
  \(L\,=\,6\,\mathrm{cm}=\,0{,}06\,\mathrm{m}\)	vzdálenost vodičů
  \(x\,=\,?\,\mathrm{(m)}\)	vzdálenost místa, kde je celková magnetická indukce nulová, od prvního vodiče

  ---

  \[x=\frac{LI_1}{(I_1+I_2)}=\frac{0{,}06{\cdot}1}{(1+2)}\,\mathrm{m}=0{,}02\,\mathrm{m}=2\,\mathrm{cm}\]

• Odpověď

  Celková magnetická indukce je nulová v bodech ležících na přímce, která je rovnoběžná s rovinou vodičů a leží uprostřed mezi vodiči ve vzdálenosti 2 cm od prvního vodiče.