Sbírka řešených úloh

Netradiční obvody 2

Úloha číslo: 304

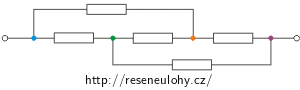
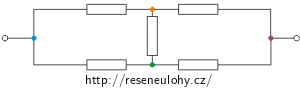
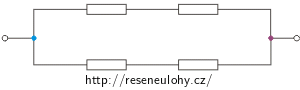
Určete celkový odpor níže nakreslených obvodů. Všechny vyznačené rezistory mají odpor R.

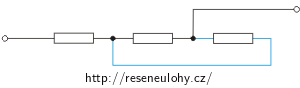
a)

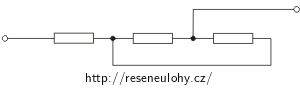
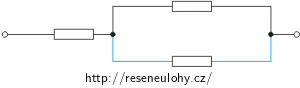
b)

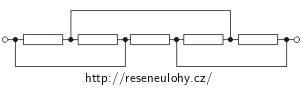
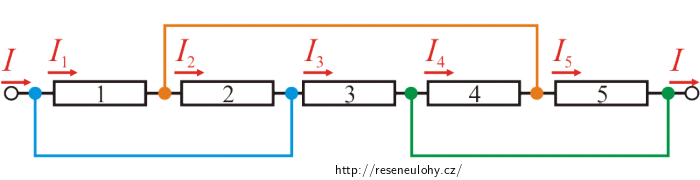
c)

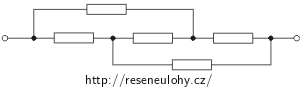
• Nápověda 1

  Nejprve si obvod překreslete do „přehlednější“ či obvyklejší podoby tak, aby bylo jasné, zda se jedná o sériové nebo paralelní zapojení rezistorů.

• Nápověda 2

  „Ohýbáním“ a zkracováním vodičů při překreslování obvodů se nemění vlastnosti obvodu, a tedy ani jeho celkový odpor.

  Rezistorem, který je zkratován vodičem, neteče proud. Všechny rezistory, jimiž neteče proud, můžeme z obvodu vynechat.

• Rozbor

  Při výpočtu celkového odporu daného zapojení je velmi důležité si zapojení správně překreslit do „jasnější“ podoby. Zde je několik triků, které lze často využít:

  1. Vodiče v zapojení můžeme ohýbat, zkracovat a prodlužovat, aniž bychom při tom ovlivnili celkový odpor obvodu. Následující dva obrázky tedy znázorňují stejné zapojení:

  

  2. Jestliže vodič propojuje dva uzly a není na něm umístěn žádný rezistor, můžeme oba uzly sloučit do jediného. Naopak také platí, že jeden uzel lze rozdělit na dva uzly propojené vodičem, na kterém není umístěn rezistor. Následující obrázky jsou opět ekvivalentní:

  

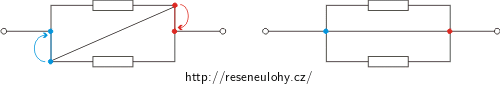
  3. Rezistory, kterými neteče proud, můžeme ze zapojení odebrat, aniž bychom tím změnili vlastnosti obvodu. Např. na levém obrázku níže teče proud jen prostřední větví paralelní části obvodu, neboť na této větvi není žádný rezistor a má tedy nulový odpor. Další dvě větve jsou tímto vodičem „vyzkratované“, neprotéká jimi žádný proud a nemají tedy vliv na celkový odpor. Proto další dva obrázky znázorňují stejné zapojení:

  

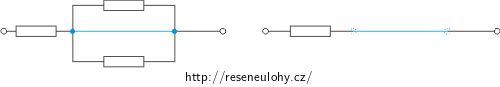
  Pomocí těchto úvah vyřešíme všechny tři zadané obvody.

  Při výpočtu celkového zapojení navíc využijeme tato pravidla:

  1. Celkový odpor obvodu s rezistory, které jsou zapojeny sériově (tj. za sebou), se rovná součtu odporů jednotlivých rezistorů.
  2. U paralelně zapojených rezistorů je převrácená hodnota celkového odporu rovna součtu převrácených hodnot jednotlivých rezistorů.

• Řešení části a)

  „Ohýbání“ a změna délky vodiče při překreslování nijak neovlivní vlastnosti zapojení, a tedy ani jeho celkový odpor.

  

  V obrázku jsme si modře vyznačili vodič, který budeme „ohýbat“, a obvod tak překreslíme do vhodnější podoby:

  

  Nyní již můžeme vypočítat celkový odpor zapojení jako součet odporu rezistoru R a odporu paralelní části.

  Paralelní část obvodu tvoří dva paralelně zapojené rezistory. Pro odpor R_p této části platí:

  \[ \frac{1}{R_\mathrm{p}}\,=\,\frac{1}{R}\,+\,\frac{1}{R} \] \[ R_\mathrm{p}\,=\,\frac{R}{2}\,. \]

  Celkový odpor zapojení:

  \[ R_\mathrm{celk}\,=\,R_\mathrm{p}\,+\,R\,=\,\frac{R}{2}\,+\,R \] \[ R_\mathrm{celk}\,=\,\frac{3R}{2}\,. \]

• Dynamický prvek – překreslení obvodu a)

  Následující aplet zobrazuje animaci překreslení obvodu.

• Řešení části b)

  U tohoto zapojení si nejprve do obrázku barevně vyznačíme uzly, které jsou propojeny vodičem bez rezistoru. Stejně barevné uzly a vodič představují vlastně jediný uzel. Navíc si do obvodu vyznačíme proudy protékající jednotlivými uzly.

  

  Nyní opět „ohýbáním“ barevně vyznačených vodičů obvod překreslíme do názornější podoby. Díky proudům procházejícím jednotlivými uzly snadno zkontrolujeme, že se jedná o zakreslení stejného obvodu.

  

  Obvod jsme tedy překreslily do podoby, z které již umíme vypočítat celkový odpor.

  Obvod je tvořen dvěma paralelními větvemi. V horní větvi jsou za sebou zapojeny dvě stejné části, z nichž každá je tvořena dvěma paralelně zapojenými rezistory. Odpor R_p obou těchto částí vypočítáme ze vztahu:

  \[ \frac{1}{R_\mathrm{p}}\,=\,\frac{1}{R}\,+\,\frac{1}{R}\,=\,\frac{2}{R} \] \[ R_\mathrm{p}\,=\,\frac{R}{2}\,. \]

  Odpor horní větve je tedy:

  \[ R_\mathrm{h}\,=\,2R_\mathrm{p}\,=\,R .\tag{horní větev}\]

  Odpor dolní větve se rovná odporu jednoho rezistoru:

  \[ R_\mathrm{d}\,=\,R .\tag{dolní větev}\]

  A pro celkový odpor zapojení platí:

  \[ \frac{1}{R_\mathrm{celk}}\,=\,\frac{1}{R_\mathrm{h}}\,+\,\frac{1}{R_\mathrm{d}}\,=\,\frac{1}{R}\,+\,\frac{1}{R}\,=\,\frac{2}{R} \] \[ R_\mathrm{celk}\,=\,\frac{R}{2}\,. \]

• Dynamický prvek – překreslení obvodu b)

  Následující aplet zobrazuje animaci překreslení obvodu.

• Řešení části c)

  Nejprve v zapojení barevně vyznačíme všechny uzly.

  

  Všimněme si, že mezi každými dvěma uzly v obvodu (kromě modrého a fialového uzlu) je zapojen jeden rezistor. Tohoto poznatku využijeme při kontrole překresleného obvodu.

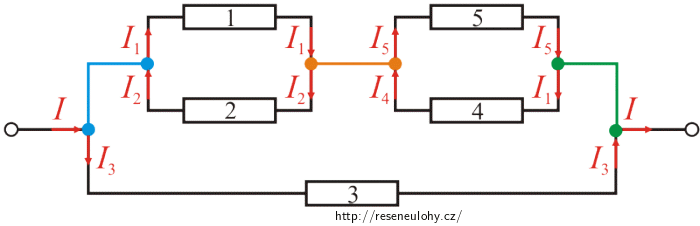
  Obvod si opět pomocí „ohýbání“ a „zkracování“ vodičů překreslíme do obvyklejší podoby.

  

  U tohoto obvodu stále není tak snadné určit jeho celkový odpor. My se ale na tento obvod ještě jednou pozorně podíváme a opět jej zjednodušíme.

  Zde je několik postřehů:

  1. Proud, který zleva vstupuje do modrého uzlu, musí opět vycházet z fialového uzlu.

  2. Obvod je symetrický.

  3. Ze symetrie obvodu vidíme, že proud protékající modrým uzlem se rozdělí na dvě stejné části, do horní a dolní větve.

  4. Stejně tak ve fialovém uzlu se spojují dva stejně velké proudy, opět z horní a dolní větve.

  Z bodu 3 a 4 vyplývá, že rezistorem mezi zeleným a oranžovým uzlem neprotéká žádný proud. Tento rezistor můžeme tedy ze zapojení odstranit, aniž bychom tak ovlivnili jeho celkový odpor.

  

  Nyní již snadno vypočítáme celkový odpor zapojení. Nejprve si určíme odpor horní větve R_h a odpor dolní větve R_d. Pro ty platí:

  \[ R_\mathrm{h}\,=\,R_\mathrm{d}\,=\,R\,+\,R\,=\,2R\,. \]

  Celkový odpor schématu:

  \[ \frac{1}{R_\mathrm{celk}}\,=\,\frac{1}{R_\mathrm{h}}\,+\,\frac{1}{R_\mathrm{d}}\,=\,\frac{1}{2R}\,+\,\frac{1}{2R}\,=\,\frac{1}{R} \] \[ R_\mathrm{celk}\,=\,R\,. \]

  Pozn.: Celkový odpor tohoto zapojení lze řešit např. i pomocí Kirchhoffových zákonů. Tento způsob řešení naleznete podrobně okomentovaný v úloze Využití Kirchhoffových zákonů pro výpočet celkového odporu zapojení.

• Dynamický prvek – překreslení obvodu c)

  Následující aplet zobrazuje animaci překreslení obvodu.

• Odpověď

  Celkové odpory jednotlivých zapojení jsou: a) \(\frac{3R}{2}\), b) \(\frac{R}{2}\), c) \(R\).

• Odkaz na podobnou úlohu

  Podívejte se také na úlohu Netradiční obvody 1, kde naleznete další tři „netradiční“ zapojení rezistorů.