Sbírka řešených úloh

Kapička mezi kovovými deskami

Úloha číslo: 19

Mezi dvěma vodorovnými kovovými deskami vzdálenými od sebe 4,8 mm a nabitými na napětí 1 kV se vznáší malá záporně nabitá olejová kapka o hmotnosti 10⁻¹³ kg.

a) Jaký je náboj kapky?

b) Kolik nadbytečných elektronů má záporně nabitá kapka oleje?

c) Kolik elektronů z celkového počtu nadbytečných elektronů kapka ztratila, jestliže se začne pohybovat směrem dolů se zrychlením o velikosti 5 m s⁻²?

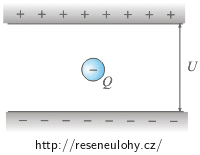
• Nápověda k části a)

  Jaké síly působí na olejovou kapku? Co pro ně musí platit, jestliže je kapka v klidu?

• Nápověda: Intenzita homogenního pole (a)

  Intenzita homogenního pole mezi dvěma vodorovnými nabitými deskami závisí na vzdálenosti desek a napětí, na které jsou desky nabity. Čím jsou desky dále od sebe a čím je mezi nimi menší napětí, tím je elektrické pole slabší.

• Rozbor: Náboj kapky (a)

  Na olejovou kapku působí směrem nahoru elektrická síla a směrem dolů síla tíhová. Protože je kapka v klidu, musí mít obě tyto síly stejnou velikost a opačný směr.

  Náboj kapky, který chceme zjistit, můžeme spočítat z velikosti elektrické síly. Ta je úměrná intenzitě elektrického pole.

  Intenzita elektrického pole mezi vodorovnými nabitými deskami je přímo úměrná napětí mezi deskami a nepřímo úměrná vzdálenosti desek.

• Řešení: Náboj kapky (a)

  Na olejovou kapku působí směrem vzhůru elektrická síla F_e = QE a směrem dolů síla tíhová F_G = mg, kde E je intenzita pole mezi deskami, Q je náboj kapky a m její hmotnost.

  

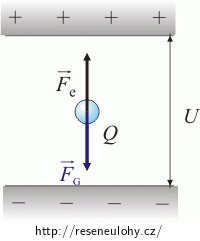
  Protože je kapka v klidu, je výslednice obou sil nulová:

  \[F_\mathrm{G} \,=\,F_\mathrm{e},\] \[mg \,=\, QE.\]

  Pro elektrickou intenzitu E platí vztah:

  \[E \,=\, \frac{U}{d}\,.\]

  Dosadíme do předchozího vztahu a vyjádříme velikost náboje kapky Q:

  \[mg \,=\, Q\,\frac{U}{d},\] \[Q \,=\, \frac {mgd}{U}.\]

• Nápověda: Počet elektronů (b)

  Velikost náboje elektronu můžeme vyhledat v tabulkách a celkový náboj jsme spočítali v bodě a).

• Řešení: Počet elektronů (b)

  Nadbytečné elektrony kapky vytvářejí její záporný náboj, který jsme spočítali v bodě a).

  Počet těchto elektronů můžeme zjistit, protože velikost náboje jednoho elektronu můžeme vyhledat:

  \[N \,=\, \frac {Q}{e},\] \[N \,=\, \frac {mgd}{Ue}.\]

• Nápověda k části c)

  1) Které ze sil působících na kapku se změnily, když kapka ztratila část náboje?

  2) Kapka se pohybuje se zrychlením a můžeme tedy využít 2. Newtonův zákon.

• Rozbor k části c)

  Jestliže kapka ztratí několik elektronů, její náboj se zmenší, a proto se zmenší elektrická síla působící směrem vzhůru. Tíhová síla zůstane stejná, jelikož hmotnost kapky se nezmění (hmotnost elektronu je velmi malá, proto změnu hmotnosti kapky zanedbáme). Výslednice elektrické a tíhové síly působí směrem dolů. Tato výslednice uděluje kapce podle druhého Newtonova zákona zrychlení (úměrné její hmotnosti), a kapka se proto začne pohybovat směrem dolů.

• Řešení části c)

  Ztratí-li kapka několik elektronů, zmenší se její náboj z Q na Q₁. Velikost elektrické síly bude F_e1 = Q₁E.

  Výslednice elektrické a tíhové síly je rovna rozdílu F_G − F_e1 a působí směrem dolů.

  Zrychlení kapky určíme z druhého Newtonova zákona:

  \[F_\mathrm{g}-{F_\mathrm{e}}_1 \,=\, m a.\tag{*}\]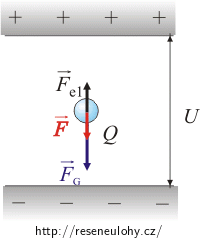

  

  Pro intenzitu homogenního pole platí stejný vztah jako v řešení části a):

  \[E \,=\, \frac {U}{d}.\]

  Dosadíme vztahy pro F_G, F_e a E do vzorce (*):

  \[m g-Q_1 E \,=\, m g,\] \[m g-Q_1 \frac{U}{d} \,=\, m a\]

  a pak výraz upravujeme, abychom vyjádřili náboj Q₁:

  \[Q_1 \frac{U}{d} \,=\, m g-m a\] \[Q_1 \,=\, \frac {m(g-a)d}{U}.\]

  Z náboje kapky už jednoduše zjistíme počet nadbytečných elektronů stejně jako v části b):

  \[N_1 \,=\, \frac{Q_1}{e}=\frac {m(g-a)d}{Ue}.\]

  Počet elektronů, které kapka ztratila, dostaneme jako rozdíl původního počtu a počtu nového:

  \[\Delta N\,=\,N-N_1,\] \[\Delta N\,=\,\frac {mgd}{Ue}\,-\,\frac {m(g-a)d}{Ue},\] \[\Delta N\,=\,\frac {mad}{Ue}.\]

• Zápis a číselný výpočet

  \(d\,=\,4{,}8 \,\mathrm{mm}\,=\,4{,}8{\cdot} 10^{-3} \,\mathrm{m}\)	vzdálenost desek
  \(U\,=1\,\mathrm{kV}\,=\,10^3 \,\mathrm{V}\)	napětí na deskách
  \(m\,=\,10^{-13} \,\mathrm{kg}\)	hmotnost kapky oleje
  \(a\,=\,5 \,\mathrm{m\,s^{-2}}\)	zrychlení kapky
  \(Q\,=\,?\,\left(\mathrm{C}\right)\)	náboj kapky
  \(N\,=\,?\)	počet nadbytečných elektronů
  \(\Delta N\,=\,?\)	počet nadbytečných elektronů u kapičky v pohybu
  Z tabulek:
  \(e\,=\,1{,}6 {\cdot} 10^{-19}\,\mathrm{C}\)
  \(g\,=\,9{,}81\,\mathrm{ m\,s^{-2}}\)

  ---

  \[Q\,=\,\frac {mgd}{U}\,=\,\frac {10^{-13}\,\cdot \,9{,}81\,\cdot \,4{,}8{\cdot} 10^{-3}}{10^3}\,\mathrm{C}\,=\,4{,}8\cdot{10^{-18}}\,\mathrm{C}\] \[N\,=\,\frac {mgd}{Ue}\,=\,\frac {10^{-13}\,\cdot \,9{,}81\,\cdot\, 4{,}8{\cdot} 10^{-3}}{10^3\,\cdot\, 1{,}6 {\cdot} 10^{-19} }=30\] \[\Delta N\,=\,\frac {mad}{Ue}\,=\,\frac {10^{-13}\,\cdot \,5\,\cdot \,4{,}8{\cdot} 10^{-3}}{10^3\,\cdot\, 1{,}6 {\cdot} 10^{-19}}\,=\,15\]

• Odpověď

  Olejová kapka má náboj 4,8·10⁻¹⁸ C, což odpovídá 30 nadbytečným elektronům.

  Když se kapka začala pohybovat se zrychlením, ztratila 15 elektronů.

• Změření elementárního náboje

  Elementární náboj e poprvé přímo změřil americký fyzik Robert A. Millikan v letech 1910 – 1913. Proměřoval síly, které působí na nabité olejové kapičky, a potvrdil, že elektrický náboj je celistvým násobkem elementárního náboje. V roce 1923 získal Nobelovu cenu za fyziku, částečně i za tuto práci.