Potenciometr

Úloha číslo: 182

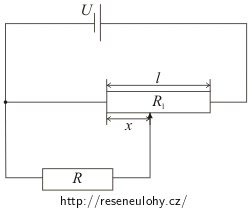
Potenciometrem zhotoveným z homogenního vodiče délky l o celkovém odporu R_l = al se mění napětí na spotřebiči o odporu R.

Určete napětí a proud rezistorem o odporu R jako funkci vzdálenosti x jezdce potenciometru od jednoho konce potenciometru.

Nápověda
Zkuste si obvod překreslit tak, že potenciometr rozdělíte na dvě části.
Rozbor
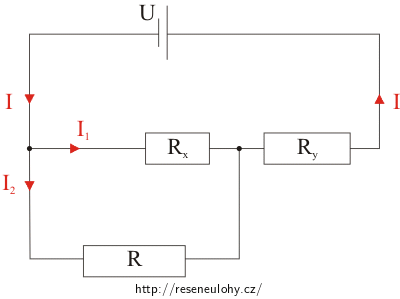
Obvod ze zadání úlohy si překreslíme tak, že potenciometr rozdělíme v místě jezdce na dvě části o odporu R_x a odporu R_y (viz Obrázek k řešení úlohy). Odpor obou částí potenciometru můžeme rovnou určit. Odpor vodiče je lineárně závislý na délce, a proto je odpor části potenciometru přímo úměrný délce vodiče, která tuto část tvoří.

Do obrázku si vyznačíme proudy, které protékají jednotlivými částmi obvodu.

Chceme určit proud I₂ procházející rezistorem R, proto si ostatní proudy pomocí I₂ vyjádříme.

Proud I je součtem proudů I₁ a I₂. A proud I₁ vyjádříme v závislosti na I₂ pomocí toho, že rezistory o odporech R a R_x jsou zapojeny paralelně, a proto na nich musí být stejný úbytek napětí.

Protože známe celkové napětí obvodu, vyjádříme si napětí zdroje jako součet úbytků napětí na rezistorech R_x a R_y.

Z rovnice pro celkové napětí si již vyjádříme proud I₂.

Napětí na rezistoru R pak vypočítáme jako součin odporu rezistoru a proudu, který tímto rezistorem prochází.
Obrázek k řešení úlohy
Obvod ze zadání úlohy si překreslíme tak, že potenciometr rozdělíme v místě jezdce na dvě části o odporu R_x a odporu R_y a do obrázku si vyznačíme proudy, které protékají jednotlivými částmi obvodu.
Řešení
Pro odpor potenciometru platí:
\[R_\mathrm{x}+R_\mathrm{y}\,=\,R_\mathrm{l}\,=\,al\,,\]
kde l je délka celého potenciometru a a je konstanta úměrnosti.

Protože odpor vodiče je lineárně závislý na délce, můžeme odpory R_x a R_y vyjádřit takto:
\[R_\mathrm{x} \,=\,ax\] \[R_\mathrm{y}\,=\,a\left(l-x\right)\,.\]
Naším cílem je určit proud I₂ procházející rezistorem R. Proto si ostatní proudy vyjádříme pomocí I₂.

Pro proud v obvodu platí, že součet proudů vstupujících do uzlu se rovná součtu proudů, které z uzlu vystupují:
\[I\,=\,I_1+I_2\,.\]
Rezistor o odporu R a část potenciometru o odporu R_x jsou zapojeny paralelně, proto platí:
\[RI_2\,=\,R_\mathrm{x}I_1\,=\,axI_1\,.\]
Vyjádříme si proud I₁:
\[I_1\,=\,\frac{R}{ax}I_2\,.\tag{*}\]
Protože známe celkové napětí, můžeme si napsat, že se napětí zdroje rovná úbytku napětí na rezistorech. Tedy:
\[U\,=\,R_\mathrm{x}I_1+R_\mathrm{y}I\,=\,axI_1+a\left(l-x\right)\left(I_1+I_2\right)\] \[U\,=\,alI_1+a\left(l-x\right)I_2\,.\]
Do této rovnice dosadíme vztah (*):
\[U\,=\,al\frac{R}{ax}I_2+a\left(l-x\right)I_2\] \[U\,=\,\left(\frac{l}{x}R+a\left(l-x\right)\right)I_2\,.\]
Konstantu úměrnosti a vyjádříme ze vztahu:
\[R_\mathrm{l}\,=\,al\hspace{10px}\Rightarrow\hspace{10px}a\,=\,\frac{R_l}{l}\,.\]
A opět dosadíme do rovnice pro celkové napětí:
\[U\,=\,\left(\frac{l}{x}R+\frac{R_\mathrm{l}}{l}\left(l-x\right)\right)I_2\,.\]
Nyní si již vyjádříme proud I₂, což je náš hledaný proud procházející rezistorem R:
\[I_2\,=\,\frac{U}{\frac{l}{x}R+\frac{R_\mathrm{l}}{l}\left(l-x\right)}\,.\]
Tuto rovnici ještě upravíme:
\[I_2\,=\,\frac{U}{\frac{l^{2}R+R_\mathrm{l}x\left(l-x\right)}{xl}}\,.\]
A získáme tak konečný vztah pro proud rezistorem v závislosti na vzdálenosti x jezdce potenciometru od jednoho konce:
\[I_\mathrm{R}\,=\,\frac{xlU}{l^2R+R_\mathrm{l}x\left(l-x\right)}\,.\]
Napětí na rezistoru se rovná součinu proudu a odporu rezistoru:
\[U_\mathrm{R}\,=\,I_\mathrm{R}R\] \[U_\mathrm{R}\,=\,\frac{xlUR}{l^2R+R_\mathrm{l}x\left(l-x\right)}\,.\]
Odpověď
Pro napětí a proud rezistorem o odporu R v závislosti na vzdálenosti x jezdce potenciometru platí:
\[I_\mathrm{R}\,=\,\frac{xlU}{l^2R+R_\mathrm{l}x\left(l-x\right)}\] \[U_\mathrm{R}\,=\,\frac{xlUR}{l^2R+R_\mathrm{l}x\left(l-x\right)}\,.\]
Odkaz na podobnou úlohu
Složitější úlohou s potenciometrem je úloha Změna proudu potenciometrem.