Metody řešení lineárních obvodů 2

Tato úloha neprošla kontrolou správnosti.

Metody řešení lineárních obvodů 2

Úloha číslo: 1895

Tato úloha slouží jako modelová pro porovnání jednotlivých metod.

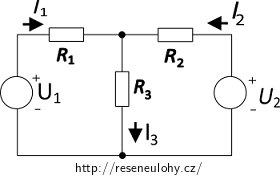
Na obrázku je nakresleno schéma zapojení se třemi rezistory \(R_1\), \(R_2\), \(R_3\) a dva stejnosměrné zdroje napětí \(U_1\), \(U_2\).

Řeště tento obvod pomocí:

a) Metody smyčkových prodů. Určete proudy I₁, I₂ a I₃.

b) Metody uzlových napětí. Určete uzlové napětí U_A a proudy I₁, I₂ a I₃.

c) Metody lineární superpozice. Určete napětí na rezistoru R₃ U₃ a proudy I₁, I₂ a I₃.

d) Théveninovou větou. Určete napětí na rezistoru R₃ U₃ a proudy I₁, I₂ a I₃.

Zadané hodnoty: R₁ = 20 Ω, R₂ = 15 Ω, R₃ = 30 Ω, U₁ = 30 V, U₂ = 15 V.

Připomenutí Kirchhoffových zákonů
Všechny metody, které se v úloze používají, vycházejí z Kirchhoffových zákonů. Pokud potřebujete, připomeňte si je zde.

Pro ty, co si chtějí jejich použití připomenout podrobněji, doporučujeme následující úlohy:
Dejte si však pozor, jaká znaménková konvence se v dané úloze používá při sestavování rovnic podle II. Kirchhoffova zákona.
Rozbor – popis jednotlivých metod
Jednotlivé metody jsou podrobně popsány v úloze Metody řešení lineárních obvodů 1. V této úloze si můžete jednotlivé metody vyzkoušet na řešení mírně odlišného obvodu.

Popisy jednotlivých metod:
a) Postup řešení
Naším úkolem je určit proudy I₁, I₂ a I₃:

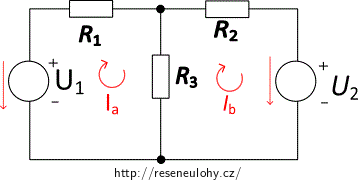
1. U zdrojů napětí si vyznačíme šipkou (na obrázku červeně) směr napětí. Pozor, jeho směr je opačný než směr elektromotorického napětí (viz poznámka u opakování Kirchhoffových zákonů).

2. Zvolíme uzavřené smyčky a jejich směr, proudy smyčkou nazveme I_a, I_b.

3. Napíšeme rovnice pro jednotlivé smyčky. Místo proudů I₁, I₂, I₃ budeme zjišťovat smyčkové proudy I_a, I_b.

4. Vyřešíme rovnice, tj. spočítáme neznámé smyčkové proudy I_a a I_b.

5. Ze smyčkových proudů I_a, I_b určíme reálné proudy I₁, I₂, I₃.
a) 1. část řešení – sestavení a vyřešení rovnic

Z druhého Kirchhoffova zákona získáme po úpravě rovnici pro smyčku I_a:
\[R_1I_\mathrm{a} + R_3(I_\mathrm{a}-I_\mathrm{b})-U_1 \,=\,0,\tag{smyčka Ia}\] \[I_\mathrm{a}(R_1 + R_3)-R_3I_\mathrm{b}\,=\,U_1.\]
Z druhého Kirchhoffova zákona získáme po úpravě rovnici pro smyčku I_b:
\[R_3(I_\mathrm{b}-I_\mathrm{a}) + R_2I_\mathrm{b} + U_2 \,=\,0,\tag{smyčka Ib}\] \[I_\mathrm{b}(R_2 + R_3)-R_3I_\mathrm{a}\,=\,-U_2.\]
Nyní máme dvě rovnice o dvou neznámých. Dosadíme do nich zadané hodnoty v základních jednotkách:
\[50I_\mathrm{a} - 30I_\mathrm{b}\,=\,30\,,\] \[-30I_\mathrm{a} + 45I_\mathrm{b}\,=\,-15.\]
Soustavu vyřešíme například pomocí sčítací metody. První rovnici vynásobíme třemi a druhou rovnici pěti a sečteme je:
\[150I_\mathrm{a} - 90I_\mathrm{b}\,=\,90, \] \[-150I_\mathrm{a} + 225I_\mathrm{b}\,=\,-75.\]
Tím jsme odstranili neznámou I_a a vypočítáme I_b:
\[135I_\mathrm{b}\,=\,15, \] \[I_\mathrm{b}\,=\, \frac{1}{9}\,\mathrm{A}.\]
Nyní dopočítáme i proud I_a:
\[ 50I_\mathrm{a} -30\cdot\frac{1}{9} \,=\,30, \] \[ 50I_\mathrm{a} \,=\,30 + \frac{10}{3}\,.\]
Tím jsme spočítali hodnotu I_a:
\[ I_\mathrm{a} \,=\,\frac{2}{3}\,\mathrm{A}.\]
a) 2. část řešení – určení reálných proudů
Nyní potřebujeme určit hodnoty reálných proudů pomocí smyčkových proudů. Použijeme I. KZ pro uzel A:
\[I_1 + I_2-I_3\,=\,0,\tag{Uzel A}\] \[I_1 + I_2\,=\,I_3. \]
Dle schématu určíme smyčkové proudy:
\[I_\mathrm{a}\,=\,I_1 \Rightarrow\, I_1\,=\,\frac{2}{3}\,\mathrm{A}, \] \[-I_\mathrm{b}\,=\,I_2 \Rightarrow\, I_2\,=\,-\frac{1}{9}\,\mathrm{A}. \]
Vyjádříme si z I. KZ proud I₃:
\[I_3\,=\,I_1+I_2, \] \[I_3\,=\,\left(\frac{2}{3}\,-\frac{1}{9}\right)\,\mathrm{A}\, = \frac{5}{9}\,\mathrm{A}.\]
a) Odpověď
Spočítali jsme smyčkové proudy \(I_\mathrm{a}\) a \(I_\mathrm{b}\):
\[I_\mathrm{a}\,=\, \frac{2}{3}\,\mathrm{A},\qquad \ I_\mathrm{b}\,=\, \frac{1}{9}\,\mathrm{A}. \]
Ze smyčkových proudů jsme určili proudy reálné \(I_1\), \(I_2\) a \(I_3\):
\[I_1\,=\, \frac{2}{3}\,\mathrm{A},\qquad \ I_2\,=\, -\frac{1}{9}\,\mathrm{A},\qquad\ I_3\,=\, \frac{5}{9}\,\mathrm{A}. \]
b) Postup řešení
Naším úkolem je určit poudy I₁, I₂ a I₃: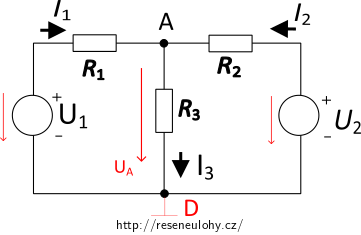

1. U zdrojů napětí si vyznačíme šipkou směr napětí.

2. V zapojení si vyznačíme jednotlivé uzly (A, D) a jeden z nich označíme jako uzel referenční (D). Referenční uzel volíme tak, aby k němu bylo připojeno co nejvíce prvků.

3. Mezi uzlem A a referenčním uzlem D vyznačíme uzlové napětí U_A.

4. Napíšeme rovnici pro uzel A dle I. Kirchhoffova zákona.

5. Proudy v jednotlivých větvích obvodu vyjádříme pomocí uzlových napětí, napětí zdrojů a odporů rezistorů. Získáme tím soustavu rovnic.

6. Řešením rovnic získáme uzlová napětí.

7. Pomocí uzlových napětí dopočítáme proudy v obvodu.
b) 1. část řešení – sestavení a vyřešení rovnic

V obvodu si označíme referenční uzel D, směry napětí zdrojů a proudy jednotlivými větvemi obvodu (viz předchozí oddíl). Napíšeme rovnici podle I. KZ pro uzel A:
\[I_1 + I_2 - I_3\,=\,0 \Rightarrow\, I_1 + I_2 \,=\,I_3. \tag{uzel A}\]
Proudy větvemi vyjádříme pomocí uzlových napětí :
\[I_\mathrm{1}\,=\, \frac{U_1-U_\mathrm{A}}{R_1}\,,\] \[I_\mathrm{2}\,=\, \frac{U_2-U_\mathrm{A}}{R_2}\,,\] \[I_3\,=\,\frac{U_\mathrm{A}}{R_3}\,\]
a to dosadíme do výše uvedené rovnice dle I. KZ:
\[\frac{U_1-U_\mathrm{A}}{R_1}\,+\frac{U_2-U_\mathrm{A}}{R_2}\,\,=\, \frac{U_\mathrm{A}}{R_3}\,.\]
Dosadíme zadané hodnoty v základních jednotkách:
\[\frac{30-U_\mathrm{A}}{20}\,+\frac{15-U_\mathrm{A}}{15}\,\,=\, \frac{U_\mathrm{A}}{30}\,.\]
Vyjádříme uzlové napětí U_A:
\[ 3(30-U_\mathrm{A}) + 4(15-U_\mathrm{A})\,=\,2U_\mathrm{A},\] \[ 90-3U_\mathrm{A} + 60 -4U_\mathrm{A}\,=\,2U_\mathrm{A},\] \[ 9U_\mathrm{A}\,=\,150,\] \[ U_\mathrm{A}\,=\, \frac{50}{3}\,\,\ \mathrm{V}. \]
Nyní můžeme dopočítat proudy.
b) 2. část řešení – dopočítání proudů
Když jsme si spočítali uzlové napětí U_A, tak proudy spočítáme velice rychle z rovnic pro jednotlivé větve (viz předchozí oddíl):
\[I_\mathrm{1}\,=\, \frac{U_1-U_\mathrm{A}}{R_1}\, \Rightarrow\, I_1 \,=\, \frac{2}{3}\, \mathrm{A},\] \[I_\mathrm{2}\,=\, \frac{U_2-U_\mathrm{A}}{R_2}\, \Rightarrow\, I_2 \,=\, -\frac{1}{9}\, \mathrm{A},\] \[I_3\,=\,\frac{U_\mathrm{A}}{R_3}\, \Rightarrow\, I_3 \,=\, \frac{5}{9}\, \mathrm{A}.\]
b) Odpověď
Spočítali jsme uzlové napětí \(U_\mathrm{A}\): \[U_\mathrm{A}\,=\, \frac{50}{3}\,\mathrm{V}.\]

Z uzlového napětí jsme určili proudy:
\[I_1\,=\, \frac{2}{3}\,\mathrm{A},\qquad \ I_2\,=\, -\frac{1}{9}\,\mathrm{A},\qquad \ I_3\,=\, \frac{5}{9}\,\mathrm{A}.\]
c) Postup řešení
Naším úkolem je určit napětí U₃:

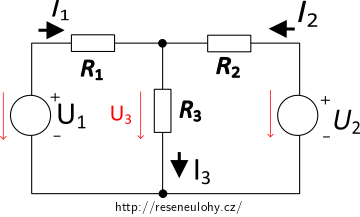
1. Vyznačíme polaritu jednotlivých zdrojů.

2. Vypočteme napětí nebo proud na uvažovaném prvku při působení jednoho zdroje, ostatní zdroje napětí nahradíme zkratem, případně jejich vnitřním odporem, a vyřadíme zdroje proudu (v našem obvodu žádné zdroje proudu nejsou).

3. To provedeme postupně pro každý zdroj.

4. Výsledné napětí nebo proud na uvažovaném prvku je pak dáno algebraickým součtem všech dílčích napětí nebo proudů.
c) 1. část řešení – zdroj U₁
Nejprve uvažujme U₁, to znamená, že zdroj U₂ nahradíme zkratem (jedná se o ideální zdroj bez vnitřního odporu).

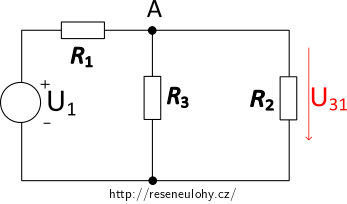
V tomto obvodu jsou rezistory R₂ a R₃ zapojeny paralelně a k nim je sériově připojen rezistor R₁. Nejdříve spočítáme paralelní zapojení rezistorů R₂ a R₃.
\[R_\mathrm{23}\,=\, \frac{R_2R_3}{R_2+R_3}\, \,=\, \frac{15 {\cdot} 30}{15+30}\,\,\mathrm{\Omega},\] \[R_\mathrm{23}\,=\, 10 \,\mathrm{\Omega}. \]
Hledané napětí U₃₁ je napětí v paralelním zapojením R₂, R_#. Víme, že napětí se na sériově zapojených rezistorech rozdělí v poměru odporů. Platí pro něj tedy:
\[U_\mathrm{31}\,=\, U_1\frac{R_\mathrm{23}}{R_\mathrm{23}+R_1},\] \[U_\mathrm{31}\,\,=\, 30\cdot\frac{10}{10+20}\,\mathrm{V}\,=\, 10 \,\mathrm{V}.\]
c) 2. část řešení – zdroj U₂
Teď uvažujme jen zdroj U₂, to znamená, že zdroj U₁ nahradíme zkratem (jedná se o ideální zdroj bez vnitřního odporu).

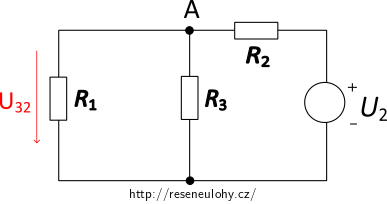
Výpočet je stejný jako v předchozím oddíle. Rezistory R₁ a R₃ jsou zapojeny paralelně a k nim je sériově připojen rezistor R₂. Odpor paralelního zapojení rezistorů R₁ a R₃ je
\[R_\mathrm{13}\,=\, \frac{R_1R_3}{R_1+R_3}\,\,=\, \frac{20{\cdot}30}{20+30}\,\,\mathrm{\Omega}\, ,\] \[R_\mathrm{13}\,=\, 12\, \mathrm{\Omega}.\]
Hledané napětí U₃₂ je napětí na paralelním zapojením R₁, R₃. Napětí se na sériově zapojených rezistorech rozdělí v poměru odporů:
\[U_\mathrm{32}\,=\, U_2\frac{R_\mathrm{13}}{R_\mathrm{13}+R_2},\] \[U_\mathrm{32}\,\,=\, 15\cdot\frac{12}{12+15}\,\,\mathrm{V}\,=\, \frac{20}{3}\,\mathrm{V} \dot{=}\, 6{,}7\,\mathrm{V}.\]
c) 3. část řešení – výsledné napětí
Nyní už máme spočítaná napětí U₃₁ a U₃₂. Vzhledem k tomu, že v obvodu se nevyskutuje další zdroj, tak výsledné napěti U₃ je dáno součtem U₃₁ a U₃₂:
\[U_\mathrm{3}\,=\, U_\mathrm{31}\ + U_\mathrm{32}\ \,=\,\frac{50}{3}\,\,\mathrm{V}.\]
c) Odpověď
Postupně jsme vypočítali napětí \(U_{31}\) a \(U_{32}\) tak, že jsme v obvodu uvažovali vždy pouze jeden zdroj:
\[U_\mathrm{31}\,=\, 10\,\mathrm{V},\qquad \ U_\mathrm{32}\,=\,\frac{20}{3}\, \mathrm{V}.\]
Výsledné napětí \(U_{3}\) je součtem obou napětí \(U_{31}\) a \(U_{32}\):
\[U_\mathrm{3}\,=\, \frac{50}{3}\,\mathrm{V}.\]
d) Postup řešení
Naším úkolem je určit napětí U₃ v obvodu:

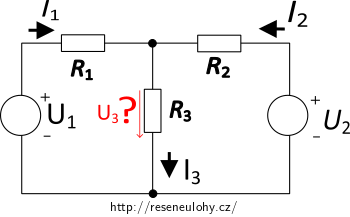
1. Podle Théveniovy věty nahradíme zbytek obvodu zdrojem napětí U₀ s vnitřním odporem R_i. Ekvivalentní obvod tedy je:

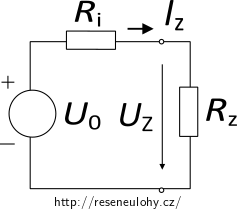
2. V ekvivalentním obvodu určíme vnitřní odpor R_i tak, že odpojíme zátěž (v našem případě odpor R₃) a zdroje napětí zkratujeme (U₁ a U₂).

3. Dále musíme určit napětí ideálního zdroje U₀, což určíme tak, že odpojíme zátěž (v našem případě odpor R₃) a určíme napětí na výstupních svorkách.

4. V ekvivalentním obvodu již známe R_i a U₀, z toho můžeme určit hledané napětí U₃.
d) 1. část řešení – vnitřní odpor R_i, napětí U₀
Dle Théveninovy věty si nakreslíme ekvivalentní obvod (viz předchozí oddíl Postup řešení).

Určíme odpor R_i tak, že zkratujeme zdroje U₁, U₂ a odpojíme zátěž R₃. Obvod si překreslíme.

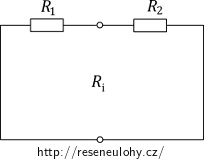
Máme dva rezistory zapojené paralelně. Určíme odpor R_i:
\[R_\mathrm{i}\,=\, \frac{R_1R_2}{R_1+R_2}\,\,=\, \frac{20{\cdot}15}{20+15}\,\mathrm{\Omega}, \] \[R_\mathrm{i}\,=\,\frac{300}{35}\,\frac{R_1R_2}{R_1+R_2}\,\mathrm{\Omega}\,\dot{=}\,8{,}6\,\mathrm{\Omega}. \]

Zbývá nám určit napětí U₀. To získáme tak, že odpojíme zátěž (rezistor R₃) a spočítáme napětí na svorkách U₀. Obvod si překreslíme.

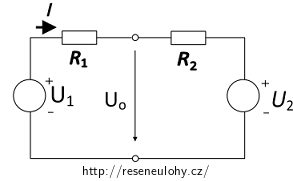
Napětí U₀ můžeme spočítat například takto:
\[U_0\,=\, U_1 - IR_1 \]
nebo takto:
\[U_0\,=\, U_2 + IR_2. \]
Tak jsme získali dvě rovnice o dvou neznámých. Dosadíme do nich zadané hodnoty v základních jednotkách:
\[U_0\,=\, 30 - 20I, \] \[U_0\,=\, 15 + 15I. \]
Soustavu vyřešíme např. sčítací metodou. První rovnici vynásobíme třemi a druhou dvěma:
\[3U_0\,=\, 90 - 60I, \] \[4U_0\,=\, 60 + 60I. \]
Rovnice sečteme:
\[7U_0\,=\, 150. \]
Tím jsme se zbavili neznámé I a vypočítáme U₀:
\[U_0\,=\, \frac{150}{7}\, \,\mathrm{V}\,\dot{=}\,21{,}42\,\,\mathrm{V}. \]
d) 2. část řešení – napětí U_z
Protože jsme v předchozím oddíle určili odpor R_i a napětí U₀ pro ekvivalentní obvod,

snadno již dopočítáme napětí U_Z (R_Z = R₃):
\[U_3=U_\mathrm{Z}\,=\, U_0\frac{R_3}{R_3+R_i}\, \,=\, \frac{150}{7}\,\cdot\,\frac{30}{\frac{60}{7}+30}\,\,,\] \[U_3\,=\, \frac{50}{3}\, \,\mathrm{V}.\]
d) Odpověď
Dle Théveninovy věty jsme si nakreslili ekvivalentní obvod. Určili jsme jeho vnitřní odpor \(R_\mathrm{i}\) a napětí \(U_0\):
\[R_\mathrm{i}\,=\, \frac{60}{7}\,\mathrm{\Omega},\qquad U_0\,=\,\frac{150}{7}\,\mathrm{V}. \]
Z ekvivalentního obvodu jsme dopočítali napětí \(U_3\):
\[U_3\,=\,\frac{50}{3} \,\mathrm{V}.\]