Paúhoř elektrický
Úloha číslo: 29
Paúhoř elektrický žije v řekách Jižní Ameriky. Živí se rybami, které zabíjí pulzem elektrického proudu. To dělá tak, že ve zvláštních buněčných článcích nazývaných elektroplaxy vytváří elektrické napětí.
Tělo paúhoře obsahuje přibližně 700 000 elektroplaxů. Elektroplax si budeme představovat jako zdroj s elektromotorickým napětím Ue = 0,15 V a vnitřním odporem Re = 0,25 Ω. A dále budeme uvažovat, že voda v okolí paúhoře má odpor Rv = 800 Ω.
a) Předpokládejme, že elektroplaxy jsou uspořádány do obdélníku, tj. tvoří n řádků a v každém řádku je m elektroplaxů. Spočtěte n a m, aby proud procházející vodou od paúhořovy hlavy k ocasu byl maximální.
b) Jak velký by byl tento proud?
Nápověda 1
Najděte si, jak se počítá napětí, proud a odpor pro paralelní a sériové zapojení.
Nápověda 2
Vyhledejte si, jak lze zjistit maximální hodnotu funkce pomocí derivace.
Obrázek
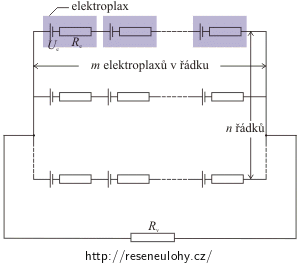
Nakreslíme si obecné schéma zapojení elektroplaxů:
n . . . počet paralelně zapojených řádků m . . . počet sériově zapojených elektroplaxů v jedné větvi N = n·m . . . počet všech elektroplaxů Ue . . . elektromotorické napětí jednoho elektroplaxu Re . . . vnitřní odpor elektroplaxu Rv . . . odpor vody v okolí paúhoře Rozbor
Pro zjištění celkového proudu procházejícího vodou použijeme Ohmův zákon. Vyjádříme si celkové napětí a celkový odpor a tím získáme rovnici pro celkový proud v závislosti na počtu elektroplaxů v řádku.
Počet elektroplaxů v jednom řádku, při kterém je proud maximální, určíme pomocí derivace. Tuto hodnotu dosadíme do obecné rovnice pro celkový proud. Výsledek se rovná hledanému maximálnímu proudu.
1. část řešení - obecná rovnice pro celkový proud
Celkový proud procházející vodou vypočítáme z Ohmova zákona
\[I_\mathrm{celk}\,=\,\frac{U_\mathrm{celk}}{R_\mathrm{celk}}\,.\]Pro paralelní zapojení platí, že elektromotorické napětí je ve všech řádcích stejné. Při sériovém zapojení zdrojů se elektromotorická napětí sčítají. Celkové elektromotorické napětí úhoře je tedy:
\[U_\mathrm{celk}\,=\,m U_\mathrm{e}\,.\]Celkový odpor získáme součtem odporu vody Rv a odporu paúhoře R.
Odpor elektroplaxů v jednom řádku: \(R_\mathrm{r}\,=\,m R_\mathrm{e}\)
a pro odpor paúhoře R platí (pro n paralelně zapojených řádků):
\[\frac{1}{R}\,=\,\frac{n}{R_\mathrm{r}}\,=\,\frac{n}{mR_\mathrm{e}}\,\Rightarrow\,R\,=\,\frac{m}{n}R_\mathrm{e}\,.\]Celkový odpor obvodu \(R_\mathrm{celk}\,=\,R_\mathrm{v}+R\,=\,R_\mathrm{v}+\frac{m}{n}R_\mathrm{e}\).
Nyní můžeme vyjádřit celkový proud Icelk:
\[I_\mathrm{celk}\,=\,\frac{U_\mathrm{celk}}{R_\mathrm{celk}}\,=\,\frac{m U_\mathrm{e}}{\frac{m}{n}R_\mathrm{e}+R_\mathrm{v}} \,=\, \frac{n m U_\mathrm{e}}{mR_\mathrm{e}+nR_\mathrm{v}}\,.\]Protože \(n m \,=\, N \), a tudíž \(n\,=\, \frac{N}{m}\), můžeme dále napsat:
\[I_\mathrm{celk}\,=\,\frac{NU_\mathrm{e}}{mR_\mathrm{e}+\frac{NR_\mathrm{v}}{m}}\,.\]Tím jsme získali vztah pro celkový proud Icelk, ve kterém je pouze jedna proměnná m.
2. část řešení - velikost m pro maximální proud
Už víme, že celkový proud procházející vodou od paúhořovy hlavy k ocasu je
\[I_\mathrm{celk}\,=\,\frac{NU_\mathrm{e}}{mR_\mathrm{e}+\frac{NR_\mathrm{v}}{m}}\,.\]Nyní potřebujeme najít takové m, aby celkový proud Icelk byl maximální. Protože čitatel zlomku je konstantní (nezávisí na m), bude zlomek maximální v případě, že je jmenovatel minimální.
Vhodnou hodnotu m nalezneme tak, že výraz ve jmenovateli zderivujeme podle m
\[\frac{\mathrm{d}}{\mathrm{d}m}\left(mR_\mathrm{e}+\frac{NR_\mathrm{v}}{m}\right)\,=\,R_\mathrm{e}+NR_v\left(-\frac{1}{m^2}\right) \,=\,R_\mathrm{e}-\frac{NR_\mathrm{v}}{m^2}\,,\]výsledek položíme roven nule
\[R_\mathrm{e}-\frac{NR_\mathrm{v}}{m^2}\,=\,0\]a vypočítáme m:
\[m^2R_\mathrm{e}-NR_\mathrm{v}\,=\,0\] \[{m}^2R_\mathrm{e}\,=\,NR_\mathrm{v}\,.\]\(m\,=\,\pm \sqrt{\frac{R_\mathrm{v}}{R_\mathrm{e}}N}\), záporná hodnota m nemá fyzikální význam.
Maximální hodnotu bude mít proud, jestliže
\[m\,=\,\sqrt{\frac{R_\mathrm{v}}{R_\mathrm{e}}N}\,.\]Zápis a číselné dosazení
N = 700 000 počet elektroplaxů Rv = 800 Ω elektrický odpor vody v okolí paúhoře Re = 0,25 Ω vnitřní odpor elektroplaxu Ue = 0,15 V elektromotorické napětí elektroplaxu n = ? počet řádků elektroplaxů tvořících tělo paúhoře m = ? počet sériově zapojených elektroplaxů v jednom řádku Imax = ? (A) maximální proud procházející vodou podél těla paúhoře
Řešení a)
Pro počet sériově zapojených elektroplaxů v jednom řádku platí:
\[m\,=\,\sqrt{\frac{R_\mathrm{v}}{R_\mathrm{e}}N}\] \[m\,=\,\sqrt{\frac{800}{0{,}25}\cdot 700\,000}\,\dot{=}\,47\,000\,. \]Pro n platí:
\[n\,=\,\frac{N}{m}\,=\,\frac{700\,000}{47\,000}\] \[n\,\dot{=}\,15\,.\]Řešení b)
Maximální proud vypočítáme dosazením za m do vztahu, který jsme odvodili v 1. části řešení
\[I_\mathrm{celk} \,=\, \frac{NU_\mathrm{e}}{mR_\mathrm{e}+\frac{NR_\mathrm{v}}{m}}\,.\]Tedy:
\[I_\mathrm{max}\,=\,\frac{700\,000\,\cdot \,0{,}15}{47\,000\,\cdot \,0{,}25 + \frac{700\,000\,\cdot \,800}{47\,000}}\, \mathrm{A}\] \[I_\mathrm{max}\,\dot{=}\,4{,}4\,\mathrm{A}\,.\]Odpověď
a) Aby byl proud procházející vodou maximální, musí elektrický obvod obsahovat 15 paralelních větví. Každá větev bude obsahovat přibližně 47 000 sériově zapojených elektroplaxů.
b) Při tomto zapojení bude mít celkový proud procházející vodou v okolí paúhořova těla hodnotu 4,4 A.
Jak je to ve skutečnosti?
Ve skutečnosti je tomu jinak.
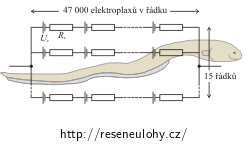
Elektroplaxy paúhoře elektrického jsou uspořádány v řádcích podél jeho těla. Každý řádek obsahuje pouze 5 000 až 6 000 článků (elektroplaxů), které jsou zapojeny sériově. Paúhoř tak umí vytvořit podél svého těla napětí asi 600 V a proud tekoucí okolní vodou může dosáhnout až jednoho ampéru.
A jak je možné, že paúhoř sám sebe neomráčí ani nezabije?
To je způsobeno tím, že proud procházející každým řádkem je malý, asi o dva řády menší než proud procházející okolní vodou. A navíc paúhoře chrání jeho tlustá kůže.
Pokud je ale paúhoř zraněný, může i sám sebe zabít elektrickým proudem.
Přehled základních vzorců pro derivování
Derivace některých jednoduchých funkcí:
Funkce Derivace \[f\left(x\right)\,=\,c\] c je konstanta \[f^,\left(x\right)\,=\,0\] \[f\left(x\right)\,=\,cx\] c je konstanta \[f^,\left(x\right)\,=\,c\] \[f\left(x\right)\,=\,x^c\] c je konstanta \[f^,\left(x\right)\,=\,cx^{c-1}\] Derivace součtu pro libovolné funkce f, g a konstanty a, b:
\[\left(af+bg\right)^,\,=\, af^,+ bg^,\,.\]Derivace součinu pro všechny funkce f, g:
\[\left(fg\right)^,\,=\,f^,g+fg^,\,.\]Derivace podílu pro všechny funkce f, g, kde g ≠ 0:
\[\left(\frac{f}{g}\right)^,\,=\,\frac{f^,g-fg^,}{g^2}\,.\]
Zpracováno v bakalářské práci Marie Snětinová (2007).
