Cívka s komplexní impedancí
Úloha číslo: 469
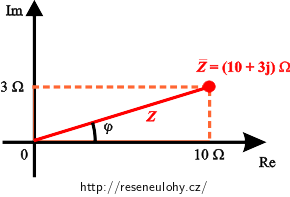
Cívka má komplexní impedanci \(\bar Z=(10{,}0+3{,}00 \mathrm{j})\mathrm \,\Omega.\)
Určete:
a) velikost impedance,
b) elektrický odpor cívky,
c) induktanci cívky,
d) amplitudu proudu v cívce, je-li na ní napětí s amplitudou 12 V,
e) fázové posunutí mezi napětím a proudem této cívky.
Pozn.: Komplexní jednotku budeme označovat j. Komplexní veličiny budeme značit pruhem nad písmenem.
Nápověda – počítání s komplexními čísly
Při řešení obvodů se střídavým proudem musíme vzít v úvahu, že napětí a proud nemusí být navzájem ve fázi. Při výpočtu můžeme použít tzv. fázory, jejichž délka odpovídá velikosti dané veličiny a jejich směr příslušnému fázovému posunutí (viz vysvětlení u úlohy Sériový RLC obvod).
Fázory ale můžeme také vyjádřit komplexními čísly, která geometricky zobrazujeme v Gaussově rovině, a nahradit tak operace s fázory, jako je jejich sčítání, operacemi s komplexními čísly.
Zopakujme si základní vlastnosti a vztahy pro komplexní čísla
Komplexní číslo \(\bar A\) můžeme vyjádřit ve tvaru algebraickém, trigonometrickém a exponenciálním:
\[{\bar A} = a \pm \mathrm{j}b = A (\cos{\varphi} \pm \mathrm{j} \sin{\varphi}) = A e^{\pm \mathrm{j} \varphi}. \]Absolutní velikost (modul) komplexního čísla odpovídá délce fázoru:
\[A = \sqrt { a^2 + b^2 }.\]Argument komplexního čísla φ odpovídá úhlu mezi fázorem a vodorovnou osou a platí pro něj vztahy:
\[\sin{\varphi} = \frac{b}{A},\] \[\cos{\varphi} = \frac{a}{A},\] \[\mathrm{tg}\,\varphi = \frac{b}{a},\] \[\mathrm{cotg}\,\varphi = \frac{a}{b}.\]Nápověda – komplexní impedance
Vyjádříme-li harmonické (sinusové) proudy a napětí pomocí fázorů a následně pomocí komplexních čísel, pak impedance, která je rovna poměru napětí a proudu, vyjde jako komplexní číslo.
\[{\bar Z} = \frac{\bar U}{\bar I} \]Tento vzorec můžeme chápat jako „obyčejný” Ohmův zákon, který platí pro obvody se stejnosměrným proudem. Místo odporu R v něm vystupuje impedance \(\bar Z\) a všechny veličiny jsou vyjádřeny komplexními čísly, nikoli reálnými.
Komplexní impedanci vyjadřujeme obvykle ve složkovém tvaru \(\bar Z =R+\mathrm{j}X\), kde R je rezistance a X je reaktance, pro kterou platí X = XL − XC. Uvědomte si, jak tento vztah koresponduje s diagramem pro impedance v sériovém zapojení.
Reaktance X je v případě impedance s indukčním charakterem kladná, v případě impedance s kapacitním charakterem je záporná.
Řešení
a) Velikost impedance Z se rovná velikosti komplexní impedance
\[\bar Z =(10{,}0+3{,}00\mathrm{j})\,\mathrm \Omega\]a vypočteme ji jako:
\[Z = \sqrt{10{,}0^2 + 3{,}00^2}\,\mathrm \Omega \dot= 10{,}4\,\mathrm \Omega. \]
b) Elektrický odpor cívky R se rovná reálné části komplexní impedance
\[\bar Z =(10{,}0+3{,}00\mathrm{j})\,\mathrm \Omega\](podrobněji viz nápověda):
\[R = 10{,}0\,\mathrm \Omega. \]
c) Induktanci XL této cívky určíme také pomocí definice komplexní impedance, která říká, že reaktance X obvodu je rovna imaginární části komplexní impedance. Protože máme do obvodu zařazenu pouze cívku, tak reaktance obvodu se rovná induktanci cívky, tj.:
\[X_\mathrm{L} = 3{,}00\,\mathrm \Omega .\]
d) Amplitudu proudu I v cívce při napětí s amplitudou 12 V získáme z Ohmova zákona, který platí i pro absolutní hodnoty (tedy velikosti) proudu, napětí i impedance:
\[I = \frac{U}{Z}=\frac{12}{10{,}4}\,\mathrm A \,\dot{=}\,1{,}15 \,\mathrm A.\]Nebo můžeme Ohmův zákon použít pro komplexní veličiny:
\[\bar I = \frac{\bar U}{\bar Z}=\frac{12}{10{,}0+3{,}00\mathrm{j}}\,\mathrm A,\]zbavíme se komplexní jednotky j ve jmenovateli zlomku:
\[\bar I = \frac{12}{10{,}0+3{,}00\mathrm{j}}\cdot \frac{10{,}0-3{,}00\mathrm{j}}{10{,}0-3{,}00\mathrm{j}}\,\mathrm A= \frac{120-36\mathrm{j} }{10^2-(3{,}00\mathrm{j})^2}\,\mathrm A =\frac{120-36 \,\mathrm j}{109}\,\mathrm A=\left(\frac{120}{109}-\frac{36}{109} \mathrm j\right)\,\mathrm A.\]Velikost amplitudy komplexního proudu má potom hodnotu:
\[I =\sqrt{\left(\frac{120}{109}\right)^2-\left(\frac{36}{109}\right)^2}\,\mathrm A \,\dot{=}\, 1{,}15 \,\mathrm A.\]Pozn.: Vidíme, že hodnoty jsou stejné jak pro výpočet s amplitudami, tak pro výpočet s komplexními čísly.
e) Fázový posun φ mezi napětím a proudem na cívce je roven argumentu komplexní impedance \[\bar Z =(10{,}0+3{,}00\mathrm{j})\,\mathrm \Omega,\] který získáme například pomocí vztahu (podrobněji viz nápověda):
\[\mathrm {tg}\,\varphi = \frac{3}{10} = 0{,}3\, \Rightarrow\, \varphi \dot= 17^{\circ}. \]Nebo fázový posun φ mezi proudem a napětím na cívce lze získat pomocí komplexního proudu, který jsme vypočítali výše: \[\bar I =(\frac{120}{109}-\frac{36}{109} \mathrm j)\,\mathrm A,\]
\[\mathrm {tg}\,\varphi' = \frac{-\frac{36}{109}}{\frac{120}{109}} \dot= -0{,}3\, \Rightarrow\, \varphi' \dot= -17^{\circ}. \]Vzhledem k tomu, že jsme fázový posun získali z komplexního proudu, tak jsme vyjádřili fázový posun mezi proudem a napětím, tj. záporné znaménko před fázovým posunutím φ značí, že proud se za napětím opožduje o 17°, ale to jinými slovy znamená, že napětí předbíhá proud. Tedy fázový posun vyšel stejně oběma postupy.
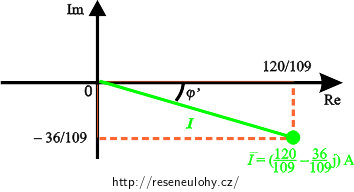
Nejlépe si znaménko u fázového posunutí ukážeme pomocí obrázku, do kterého je v Gaussově rovině zakreslena komplexní impedance a komplexní proud. Hodnota napětí je reálná, a proto leží na reálné ose v kladném směru (vzhledem k rozdílným jednotkám impedance a napětí není napětí zakreslené přímo v obrázku).
Odpověď
Velikost impedance cívky se zadanou komplexní impedancí je přibližně 10,4 Ω, elektrický odpor cívky je 10,0 Ω a induktance cívky je 3,00 Ω. Při napětí 12 V cívkou protéká proud o velikosti asi 1,15 A. Fázový posun mezi napětím a proudem je přibližně 17°.


