Paralelní zapojení rezistoru a cívky
Úloha číslo: 622
Ke zdroji střídavého napětí o efektivní hodnotě 120 V je připojena zátěž tvořená paralelní kombinací rezistoru s odporem 1 kΩ a ideální cívkou s indukčností 630 mH. Ze zdroje je odebírán proud o efektivní hodnotě 0,5 A. Určete frekvenci napětí a proud procházející ideální cívkou.
Zápis
U = 120 V efektivní hodnota napětí R = 1 kΩ odpor rezistoru L = 630 mH indukčnost cívky I = 0,5 A efektivní hodnota proudu f = ? (Hz) frekvence napětí obvodu IL = ? (A) efektivní hodnota proudu protékajícího cívkou Nápověda – schéma zapojení
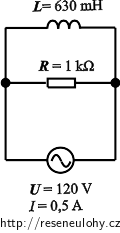
Nápověda
Daný obvod je paralelní zapojení rezistoru a cívky, proto je lepší pracovat s admitancemi než impedancemi.
V paralelních obvodech získáme celkovou admitanci jako součet dílčích admitancí a Ohmův zákon nabývá tvaru:
\[ I = UY.\]Více naleznete v úloze Celková admitance v obvodu.
Pokud ale s admitancemi neumíte pracovat a ani se to nechcete naučit, lze úlohu vyřešit i bez nich pomocí impedancí a fázorových diagramů.
Rozbor
Frekvenci napětí zdroje získáme pomocí Ohmova zákona pro střídavý proud pro celý obvod. Jelikož se jedná o paralelní zapojení, ve kterém je v jednotlivých větvích obvodu stejné napětí, vyjádříme si celkovou admitanci obvodu. Tu získáme jako součet jednotlivých admitancí prvků v obvodu zařazených. Celkovou admitanci dosadíme do Ohmova zákona, ze kterého vyjádříme hledanou frekvenci.
Proud protékající cívkou získáme pomocí Ohmova zákona pro obvod se střídavým proudem, který ale aplikujeme pouze na větev s cívkou.
Bez použití admitancí: Pomocí fázorového diagramu si vyjádříme vztah mezi celkovým proudem a proudy rezistorem a cívkou. Protože se jedná o paralelní zapojení, jsou napětí na cívce i rezistoru stejná jako napětí zdroje. Proud rezistorem tedy vyjádříme pomocí Ohmova zákona a po dosazení vyjádříme hledaný proud cívkou.
Z proudu cívkou a napětí vyjádříme pomocí Ohmova zákona induktanci cívky a z ní pomocí zadané indukčnosti určíme frekvenci zdroje.
Řešení s využitím admitancí
Pro výpočet frekvence napětí použijeme Ohmův zákon pro střídavý proud:
\[ I = \frac{ U}{Z}= U Y, \]kde Z je celková impedance obvodu a Y celková admitance obvodu. Jedná se o paralelní zapojení, proto je výhodnější pracovat s admitancí.
Celkovou admitanci obvodu získáme jako součet admitance cívky YL a admitance rezistoru YR.
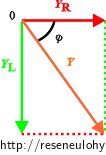
Z diagramu je vidět, že platí
\[ Y = \sqrt{ Y_\mathrm{L}^2 + Y_\mathrm{R}^2} \]a po dosazení do Ohmova zákona dostáváme
\[ I = U \sqrt{ Y_\mathrm{L}^2 + Y_\mathrm{R}^2}. \]Pro admitanci cívky YL platí
\[ Y_\mathrm{L} = \frac{1}{X_\mathrm{L}}=\frac{1}{\omega L}=\frac{1}{2 \pi f L}, \]kde XL je induktance cívky, ω úhlová frekvence napětí, f frekvence napětí a L indukčnost cívky. Pro admitanci rezistoru YR platí
\[ Y_\mathrm{R} = \frac{1}{R}, \]kde R je odpor rezistoru. Oba vztahy dosadíme do Ohmova zákona:
\[ I = U \sqrt{ (\frac{1}{2 \pi f L})^2 + ( \frac{1}{R})^2}. \]Odtud postupně vyjádříme frekvenci f:
\[ \frac{I}{U} = \sqrt{ (\frac{1}{2 \pi f L})^2 + ( \frac{1}{R})^2}. \]Umocníme obě strany rovnice:
\[ (\frac{I}{U})^2 = (\frac{1}{2 \pi f L})^2 + ( \frac{1}{R})^2, \]osamostatníme člen, ve kterém vystupuje frekvence f:
\[ (\frac{I}{U})^2-( \frac{1}{R})^2 = (\frac{1}{2 \pi f L})^2, \] \[ \frac{R^2 I^2 - U^2}{U^2 R^2} = (\frac{1}{2 \pi f L})^2 , \]vyjádříme frekvenci f:
\[ (2 \pi f L)^2 = \frac{U^2 R^2}{R^2 I^2 - U^2} \] \[ f^2 = \frac{U^2 R^2}{(2 \pi L)^2(R^2 I^2 - U^2)} \] \[ f = \frac{U R}{2 \pi L \,\sqrt{R^2 I^2 - U^2}}. \]
Pro výpočet efektivní hodnoty proudu protékajícího cívkou IL použijeme také Ohmův zákon pro střídavý proud:
\[ I_\mathrm{L} = \frac{U}{X_\mathrm{L}} = \frac{U}{2 \pi f L}, \]kde U je efektivní hodnota napětí na cívce, která je stejná jako na zdroji. Dosadíme za frekvenci f:
\[ I_\mathrm{L} = \frac{U}{2 \pi L} \frac{2 \pi L\sqrt{R^2 I^2 - U^2}} {U R}= \frac{\sqrt{R^2 I^2 - U^2}}{R} .\]
Číselné dosazení:
\[ f = \frac{U R}{2 \pi L\,\sqrt{R^2 I^2 - U^2}} = \frac{120 {\cdot} 10^3}{2\cdot \pi \cdot 0{,}63\cdot\sqrt{10^6 {\cdot} 0{,}5^2 - 120^2}}\,\mathrm {Hz}\, \dot=\, 62\,\mathrm {Hz} \] \[ I_\mathrm{L} = \frac{\sqrt{R^2 I^2 - U^2}}{R}= \frac{\sqrt{10^6 {\cdot} 0{,}5^2 - 120^2}}{10^3}\,\mathrm A \,\dot=\, 0{,}49\,\mathrm A \]Řešení bez využití admitancí
Proud protékající cívkou lze získat také pomocí fázorového diagramu pro paralelní zapojení cívky a rezistoru:
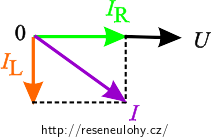
V diagramu jeU efektivní hodnota napětí (stejná pro všechny větve), IR proud protékající rezistorem (ve fázi s napětím), IL proud protékající cívkou (opožďující se za napětím) a I je efektivní hodnota proudu zdrojem. Z diagramu je vidět, že celkový proud získáme jako
\[I^2 = I_\mathrm{R}^2 + I_\mathrm{L}^2 .\]Vyjádříme si proud tekoucí cívkou IL:
\[I_\mathrm{L} = \sqrt{I^2 - I_\mathrm{R}^2}.\]Pro proud tekoucí rezistorem IR platí podle Ohmova zákona
\[I_\mathrm{R} = \frac{U}{R},\]kde R je odpor rezistoru. To dosadíme do předchozího vztahu:
\[I_\mathrm{L} = \sqrt{I^2 - (\frac{U}{R})^2}.\]Dostáváme tak hledaný vztah pro proud cívkou IL.
Frekvenci napětí zdroje získáme pomocí Ohmova zákona pro obvod se střídavým napětím, který aplikujeme na cívku:
\[U = X_\mathrm{L} I_\mathrm{L}, \]kde XL = ωL = 2πfL je induktance cívky. Dosadíme a vyjádříme frekvenci napětí zdroje f:
\[U = 2 \pi f L I_L \] \[U = 2 \pi f L \sqrt{I^2 - (\frac{U}{R})^2} \] \[ f = \frac{U}{2 \pi L \sqrt{I^2 - (\frac{U}{R})^2}}.\]
Číselné dosazení:
\[I_\mathrm{L} = \sqrt{I^2 - (\frac{U}{R})^2}=\sqrt{0{,}5^2 - (\frac{120}{1000})^2}\,\dot=\,0{,}49\,\mathrm A\] \[ f = \frac{U}{2 \pi L \sqrt{I^2 - (\frac{U}{R})^2}}=\frac{120}{2 \cdot \pi \cdot 0{,}63 \cdot \sqrt{0{,}5^2 - (\frac{120}{1000})^2}}\,\dot=\,62\,\mathrm {Hz}\]Odpověď
Frekvence napětí zdroje je přibližně 62 Hz a efektivní hodnota proudu protékajícího cívkou je asi 0,49 A.

