Sbírka řešených úloh

Výpočet proudů v obvodu při konstantním výkonu

Úloha číslo: 79

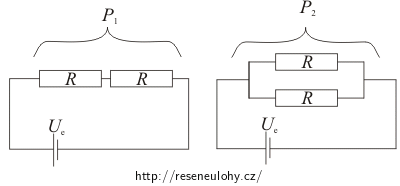
Dva rezistory o odporu 10 Ω jsou připojeny ke zdroji o elektromotorickém napětí 3 V. Nejprve tyto rezistory zapojíme do série, poté paralelně. Při obou zapojeních je výkon elektrického proudu v rezistorech stejný. Určete proudy, které v obou případech procházejí obvodem.

• Nápověda 1

  Uvědomte si, že používáme reálný zdroj napětí, tedy zdroj napětí s vnitřním odporem.

• Nápověda 2

  Vyhledejte si, co nám říká Ohmův zákon pro uzavřený obvod.

• Řešení nápovědy 2

  Na vnitřním odporu zdroje dojde k úbytku napětí R_iI. Část elektromotorického napětí U_e se tedy „ztrácí“ na vnitřním odporu zdroje, a proto se napětí U na vnější části obvodu rovná

  \[U\,=\,U_\mathrm{e}\,-\,R_\mathrm{i}I\,.\]

• Rozbor

  Ohmův zákon pro uzavřený obvod:

  Na vnitřním odporu zdroje dojde k úbytku napětí R_iI. Proto se napětí na spotřebiči (tj. na vnější části obvodu) rovná rozdílu elektromotorického napětí zdroje a úbytku napětí na vnitřním odporu zdroje.

  Odpor vnější části obvodu:

  Pro sériově zapojené rezistory platí, že celkový odpor je roven součtu odporů jednotlivých rezistorů. Pokud jsou rezistory řazeny paralelně, je převrácená hodnota celkového odporu rovna součtu převrácených hodnot odporů v jednotlivých větvích.

  Výkon elektrického proudu na spotřebiči:

  Výkon elektrického proudu na spotřebiči je přímo úměrný odporu spotřebiče a druhé mocnině proudu, který prochází spotřebičem.

  Výpočet vnitřního odporu zdroje:

  Ze zadání úlohy víme, že výkony elektrického proudu na rezistorech jsou pro oba obvody stejné. Jejich porovnáním vypočítáme vnitřní odpor zdroje. Dosazením do Ohmova zákona pak dopočítáme proudy procházející obvody.

• Řešení výpočtem

  Výkon elektrického proudu na spotřebiči je přímo úměrný odporu spotřebiče a druhé mocnině proudu, který prochází spotřebičem:  P = RI².

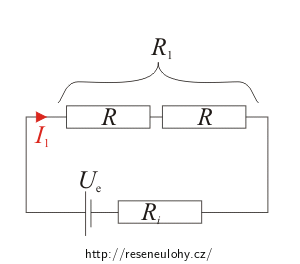
  	Pro sériově zapojené rezistory platí: \[R_1\,=\,R+R\,=\,2R\] \[P_1\,=\,R_1I_1^2\,=\,2RI_1^2\]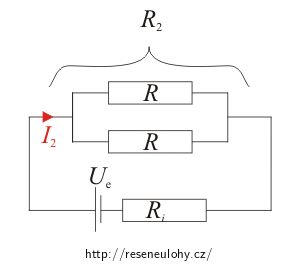
  	Pro paralelně zapojené rezistory: \[\frac{1}{R_2}\,=\,\frac{1}{R}+\frac{1}{R}\,=\,\frac{2}{R}\hspace{5px}\Rightarrow\hspace{5px}R_2\,=\,\frac{R}{2}\] \[P_2\,=\,R_2I_2^2\,=\,\frac{R}{2}I_2^2\]

  Při obou zapojeních je výkon elektrického proudu v rezistorech stejný:

  \[P_1\,=\,P_2\] \[2RI_1^2\,=\,\frac{R}{2}I_2^2\] \[4I_1^2\,=\,I_2^2\,.\]

  Po odmocnění této rovnice zjistíme, že proud I₁, procházející prvním obvodem, je dvakrát menší než prou I₂, který teče druhým obvodem:

  \[2I_1\,=\,I_2\,.\tag{1}\]

  Podle Ohmova zákona pro uzavřený obvod platí:

  \[ I_1\,=\,\frac{U_\mathrm{e}}{R_1+R_\mathrm{i}}\,=\,\frac{U_\mathrm{e}}{2R+R_\mathrm{i}} \] \[ I_2\,=\,\frac{U_\mathrm{e}}{R_2+R_\mathrm{i}}\,=\,\frac{U_\mathrm{e}}{\frac{R}{2}+R_\mathrm{i}}\,. \]

  Takto vyjádřené proudy dosadíme do rovnice (1):

  \[ 2\,\frac{U_\mathrm{e}}{2R+R_\mathrm{i}}\,=\,\frac{U_\mathrm{e}}{\frac{R}{2}+R_\mathrm{i}} \]

  a určíme vnitřní odpor zdroje R_i:

  \[ 2\,\frac{1}{2R+R_\mathrm{i}}\,=\,\frac{1}{\frac{R}{2}+R_\mathrm{i}} \] \[ 2\,\left(\frac{R}{2}+R_\mathrm{i}\right)\,=\,2R+R_\mathrm{i} \] \[ R+2R_\mathrm{i}\,=\,2R+R_\mathrm{i} \] \[ R_\mathrm{i}\,=\,R\,. \]

  Nyní již číselně dopočítáme proudy I₁ a I₂:

  \[I_1\,=\,\frac{U_\mathrm{e}}{2R+R_\mathrm{i}}\,=\,\frac{U_\mathrm{e}}{2R+R}\,=\,\frac{U_\mathrm{e}}{3R}\,=\, \frac{3\,\mathrm{V}}{3{\cdot}10\,\mathrm{\Omega}}\,=\,0{,}1\,\mathrm{A}\,.\]

  Z rovnice (1) víme, že proud I₂ je dvakrát větší, tedy:

  \[I_2\,=\,0{,}2\,\mathrm{A}\,.\]

• Řešení úvahou

  Při sériovém zapojení dvou stejných rezistorů je jejich celkový odpor dvakrát větší než odpor každého z nich. Pokud rezistory spojíme paralelně, pak je celkový odpor roven jedné polovině odporu jednoho rezistoru. Odpor sériového zapojení je tedy čtyřikrát větší než paralelního.

  Výkon elektrického proudu na spotřebiči je přímo úměrný odporu spotřebiče a druhé mocnině proudu, který spotřebičem protéká. Ze zadání úlohy víme, že se při sériovém a paralelním zapojení rezistorů výkony elektrického proudu v rezistorech rovnají. Druhá mocnina proudu procházejícího obvodem se sériovým zapojením je tedy čtyřikrát menší než druhá mocnina proudu procházejícího obvodem, ve kterém jsou rezistory zapojeny paralelně. A proto: Celkový proud sériovým zapojením musí být poloviční než celkový proud paralelním zapojením.

  Z Ohmova zákona pro uzavřený obvod víme, že proud protékající obvodem je roven podílu elektromotorického napětí zdroje a součtu odporů vnější a vnitřní části obvodu (tj. součtu celkového odporu rezistorů a vnitřního odporu zdroje). Proud protékající obvodem je tedy nepřímo úměrný součtu odporů vnější a vnitřní části obvodu.

  Z toho vyplývá, že součet odporů vnitřní a vnější části obvodu při sériovém řazení rezistorů je dvakrát větší než součet těchto odporů při paralelním zapojení:

  \[R_1+R_\mathrm{i} \,=\,2\left(R_2+R_\mathrm{i}\right)\,.\tag{*}\]

  V prvním odstavci jsme si odvodili, že celkový odpor při sériovém zapojení je dvojnásobek odporu rezistoru a při paralelním zapojení je celkový odpor polovina odporu rezistoru:

  \[R_1\,=\,2R\] \[R_2\,=\,\frac{1}{2}R\,.\]

  Dosadíme-li tyto dvě rovnice do rovnice (*), zjistíme, že vnitřní odpor zdroje je stejný jako odpor jednoho rezistoru.

  Z Ohmova zákona pro uzavřený obvod nyní dopočítáme číselnou hodnotu proudu I₁:

  \[I_1\,=\,\frac{U_\mathrm{e}}{R_1+R_\mathrm{i}}\,=\,\frac{U_\mathrm{e}}{2R+R}\] \[I_1\,=\,\frac{U_\mathrm{e}}{3R}\,=\,\frac{3\,\mathrm{V}}{3\,\cdot10\,\mathrm{\Omega}}\,=\,0{,}1\,\mathrm{A}\,.\]

  Proud I₂ je dvakrát větší než I₁:

  \[I_2\,=\,0{,}2\,\mathrm{A}\,.\]

• Odpověď

  Obvodem se sériově zapojenými rezistory protéká proud 0,1 A, obvodem s paralelně zapojenými rezistory proud 0,2 A.

• Odkaz na podobnou úlohu

  Tuto úlohu můžeme také řešit podobně jako úlohu Výkon elektrického proudu.