Magnetické pole solenoidu

Úloha číslo: 451

Určete vztah pro velikost magnetické indukce magnetického pole solenoidu, který má n závitů na 1 m své délky a prochází jím elektrický proud I.

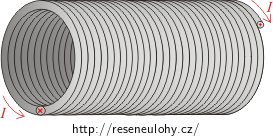
Nápověda - Solenoid
Solenoid je tvořen dlouhým vodičem, který je hustě navinut tak, že vytváří šroubovici válcového tvaru a kruhového průřezu. Délka solenoidu je mnohem větší než jeho průměr, takže můžeme zanedbat rušivý vliv začátku či konce vinutí.

Solenoid je charakterizován počtem závitů N a délkou l. Odtud počet závitů na jednotku délky n je
\[n=\frac{N}{l}.\]
Nápověda - Magnetické pole solenoidu
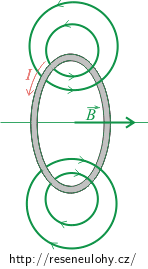
Průběh magnetického pole solenoidu můžeme odhadnout z magnetického pole jednotlivých závitů, kterými prochází elektrický proud. V případě solenoidu se pole jednotlivých závitů sčítají.
Nápověda - Ampérův zákon
Ampérův zákon se používá k výpočtu velikosti vektoru magnetické indukce \(\vec{B}\) v některých symetrických případech podobně, jako se používá Gaussova věta k výpočtu velikosti vektoru elektrické intenzity \(\vec{E}\) v symetrických případech v elektrostatice.

Matematická podoba Ampérova zákona zní
\[\int_l \vec{B}\cdot \,\mathrm{d}\vec{l}=\mu_\mathrm{0} I_\mathrm{c},\]
kde I_c značí celkový proud uzavřený Ampérovou smyčkou l.
Rozbor
Průběh magnetického pole solenoidu můžeme určit z průběhu pole jednotlivých závitů. V případě dostatečně dlouhého a hustě vinutého solenoidu se pole od jednotlivých závitů sčítá tak, že uvnitř solenoidu dostaneme homogenní magnetické pole.

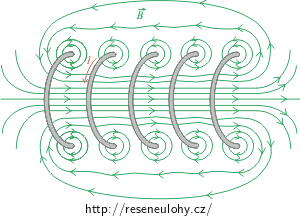
Vektor magnetické indukce popisující pole uvnitř solenoidu směřuje podél osy solenoidu. Směr určíme pomocí pravidla pravé ruky. Vně solenoidu jsou příspěvky od protilehlých částí každého závitu opačně orientované, působí proti sobě a pole je podstatně méně intenzivní než uvnitř solenoidu, takže ho můžeme v případě dlouhého solenoidu zanedbat. Na základě této úvahy určíme pole uvnitř solenoidu pomocí Ampérova zákona (viz nápověda).
Řešení
Magnetické pole vně solenoidu budeme považovat za přibližně nulové a uvnitř solenoidu bude pole homogenní (detailnější odvození je uvedeno v předchozím oddíle). Velikost magnetické indukce potom určíme pomocí Ampérova zákona:
\[\int_\mathrm{l} \vec{B}\cdot \,\mathrm{d}\vec{l}=\mu_\mathrm{0} I_\mathrm{c}.\tag{1}\]
Jako uzavřenou Ampérovu křivku zvolíme obdélník ABCD se stranami délky h rovnoběžnými s osou solenoidu.

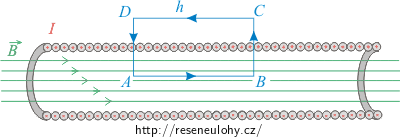
Integrál na levé straně Ampérova zákona lze rozdělit na součet čtyř integrálů, každý pro jeden ze čtyř úseků pravoúhlé křivky:
\[\int_\mathrm{ABCD} \vec{B}\cdot \,\mathrm{d}\vec{l}=\int_\mathrm{A}^\mathrm{B} \vec{B}\cdot \,\mathrm{d}\vec{l}+\int_\mathrm{B}^\mathrm{C} \vec{B}\cdot \,\mathrm{d}\vec{l}+\int_\mathrm{C}^\mathrm{D} \vec{B}\cdot \,\mathrm{d}\vec{l}+\int_\mathrm{D}^\mathrm{A} \vec{B}\cdot \,\mathrm{d}\vec{l}.\tag{2}\]
První integrál na pravé straně rovnice (2) má tvar
\[\int_\mathrm{A}^\mathrm{B} \vec{B}\cdot \,\mathrm{d}\vec{l}=Bh.\]
Druhý a čtvrtý integrál jsou rovny nule, protože pro každý délkový element těchto úseků je magnetická indukce \(\vec{B}\) buď kolmá k úseku, nebo nulová, takže skalární součin je roven nule:
\[\vec{B}\,\cdot\, \mathrm{d}\vec{l}=0.\]
Třetí integrál podél úsečky CD, která leží mimo solenoid, je nulový, neboť zde je velikost magnetické indukce nulová.

Pro celou pravoúhlou křivku tedy dostáváme
\[\int_\mathrm{l} \vec{B}\cdot \,\mathrm{d}\vec{l}=Bh.\]
Výsledný proud I_c uzavřený v pravoúhlé Ampérově křivce není pouze proud I, neboť uvnitř obdélníku se nachází více než jeden závit. Označíme-li počet závitů na jednotku délky n, je
\[I_\mathrm{c}=nhI\]
a z Ampérova zákona plyne
\[Bh=\mu_\mathrm{0} nhI,\]
a tedy pro velikost magnetické indukce platí
\[B=\mu_\mathrm{0} In.\]
Komentář - Velikost magnetické indukce reálného solenoidu
V solenoidu konečné délky je pole poblíž konců slabší a rozbíhá se. I když jsme rovnici pro velikost magnetické indukce
\[B=\mu_\mathrm{0} In\]
odvodili pro nekonečně dlouhý ideální solenoid, platí i pro reálný solenoid konečné délky, zajímá-li nás magnetická indukce v bodech uvnitř solenoidu dostatečně daleko od jeho konců.

Jak jsme odvodili, velikost magnetické indukce uvnitř solenoidu nezávisí na průměru solenoidu a je konstantní v celém jeho průřezu. Solenoidem můžeme vytvořit homogenní magnetické pole podobně, jako dvěma rovnoběžnými deskami kondenzátoru vytvoříme homogenní elektrické pole.
Odpověď
Odvodili jsme vztah pro velikost magnetické indukce magnetického pole solenoidu s proudem. Tento vztah má tvar
\[B=\mu_\mathrm{0} In.\]