Magnetická indukce na ose kruhového závitu
Úloha číslo: 395
Nalezněte vztah pro velikost magnetické indukce v libovolném bodě P ležícím na ose kruhového závitu, kterým prochází konstantní elektrický proud.
Nápověda
Nakreslete si obrázek závitu s proudem a zvolte si libovolný bod P na ose závitu. Závit rozdělte na malé části. Každá část závitu přispívá v bodě P k magnetickému poli. Celková magnetická indukce v bodě P je rovna součtu všech příspěvků od jednotlivých částí závitu. Zvolíme dílky na závitu velmi malé a výslednou magnetickou indukci určíme integrací přes všechny příspěvky úseků vodiče.
Nakreslete si do obrázku, kterým směrem míří příspěvky od několika částí závitu, a určete směr celkové magnetické indukce.
Rozbor
Velikost magnetické indukce v libovolném bodě P ležícím na ose proudové smyčky určíme pomocí Biotova-Savartova zákona.
Budeme uvažovat příspěvky od jednotlivých částí proudové smyčky k magnetické indukci v bodě P. Celková velikost magnetické indukce v bodě P pak bude dána integrálem přes všechny příspěvky proudové smyčky. Dostaneme tak vztah pro velikost magnetické indukce v libovolně zvoleném bodě P na ose smyčky.
Pro získání velikosti magnetické indukce ve středu smyčky jen posuneme bod P do středu závitu a za vzdálenost bodu, ve kterém jsme vyjádřili velikost magnetické indukce, dosadíme nulu.
Řešení
Příspěvky \(\mathrm{d}\vec{B}\) od jednotlivých částí kruhového závitu určíme z Biotova-Savartova zákona, jehož tvar je:
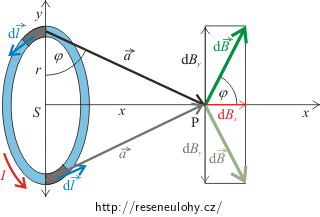
\[\mathrm{d}\vec{B} = \frac{\mu_0}{4\pi}\, \frac{I\, \mathrm{d}\vec{l}\times \vec{a}}{a^{3}}.\]Z vektorového součinu a pravidla pravé ruky plyne, že magnetická indukce \(\mathrm{d}\vec{B}\) vytvořená v bodě P proudovým elementem \(I\mathrm{d}\vec{l}\), je kolmá k rovině tvořené vektory \(\vec{a}\) a \(\mathrm{d}\vec{l}\) (viz obrázek). Příspěvky \(\mathrm{d}\vec{B}\) od všech částí kruhového závitu budou ležet na kuželu, jehož osou je osa x.
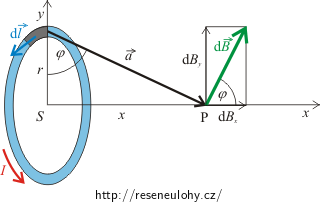
Složky \(\mathrm{d}B_\mathrm{y}\) vektoru \(\mathrm{d}\vec{B}\) pocházejících od protilehlých elementů závitu se vyruší. Celková magnetická indukce \(\vec{B}\) smyčky v bodě P tedy směřuje podél osy smyčky a její velikost je:
\[B=B_\mathrm{x}=\int_l{\mathrm{d}B_\mathrm{x}},\]kde \(\mathrm{d}B_\mathrm{x}=\mathrm{d}B\, \cos{\varphi}\) a integrujeme ji podél celé smyčky.
Velikost \(\mathrm{d}B\) vyjádříme pomocí Biotova-Savartova zákona jako:
\[\mathrm{d}B = \frac{\mu_0}{4\pi}\, \frac{I| \mathrm{d}\vec{l}\times \vec{a}|}{a^{3}}.\]Pro velikost vektorového součinu platí \(|\mathrm{d}\vec{l}\times\vec{a}|=(\mathrm{d}l\,a\,\sin{\alpha})\), kde úhel α je úhel mezi vektory \(\mathrm{d}\vec{l}\) a \(\vec{a}\). Vektor elementu závitu \(\mathrm{d}\vec{l}\) je kolmý k vektoru \(\vec{a}\) (viz obrázek). Velikost vektorového součinu \(|\mathrm{d}\vec{l}\times\vec{a}|\) je tedy:
\[|d\vec{l}\times\vec{a}|=\mathrm{d}l\,a\, \sin {90^\circ}=\mathrm{d}l\,a.\]Velikost vektoru a vyjádříme z pravoúhlého trojúhelníka pomocí Pythagorovy věty jako:
\[a=\sqrt{r^2+x^2}.\]Velikost úhlu cos φ určíme také pomocí pravoúhlého trojúhelníka:
\[\cos{\varphi}=\frac{r}{a}=\frac{r}{\sqrt{r^2+x^2}}.\]Vyjádřené vztahy dosadíme do Biotova-Savartova zákona a upravíme:
\[B=\int_\mathrm{l}{\mathrm{d}B\, \cos{\varphi}}=\int_\mathrm{l}\frac{\mu_0}{4\pi}\, \frac{I\, \mathrm{d}l\, a}{a^{3}}\,\frac{r}{a}=\int_\mathrm{l}\frac{\mu_0}{4\pi}\, \frac{Ir\, \mathrm{d}l}{({r^2+x^2})^{\frac{3}{2}}}.\]Výraz integrujeme podél celé kružnice. Integrační proměnná je tedy dl, vše ostatní ve vzorci jsou konstanty, které můžeme vytknout před integrál:
\[B=\frac{\mu_0}{4\pi}\, \frac{I\,r}{\left({r^2+x^2}\right)^{\frac{3}{2}}}\int_\mathrm{l}{\mathrm{d}l}.\]Po zintegrování dostáváme pro velikost magnetické indukce B výraz:
\[B=\frac{\mu_0}{4\pi}\, \frac{Ir}{\left({r^2+x^2}\right)^{\frac{3}{2}}}\,l.\tag{*}\]Délka proudové smyčky l se rovná obvodu kružnice o poloměru r:
\[B=\frac{\mu_0}{4\pi}\, \frac{ 2\pi Ir^2}{\left({r^2+x^2}\right)^{\frac{3}{2}}}.\]Po úpravě výrazu získáváme vztah pro velikost magnetické indukce B v libovolném bodě P ležícím ve vzdálenosti x od středu závitu na ose závitu:
\[B=\frac{\mu_0}{2}\, \frac{I r^2}{\left({r^2+x^2}\right)^{\frac{3}{2}}}.\]Poznámka: Pro velikost magnetické indukce ve středu závitu s proudem posuneme bod P do středu závitu. Za vzdálenost x bodu P od středu závitu tedy dosadíme x = 0. Pro velikost magnetické indukce Bs ve středu závitu platí:
\[B_\mathrm{s}=\frac{\mu_0}{2}\,\frac{I}{r}.\]Odpověď
Pro velikost magnetické indukce v libovolném bodě P ležícím na ose závitu, kterým prochází konstantní elektrický proud, platí:
\[B=\frac{\mu_0}{2}\, \frac{I r^2}{\left({r^2+x^2}\right)^{\frac{3}{2}}}.\]Vektor magnetické indukce \(\vec{B}\) v bodě P směřuje podél osy závitu.
Magnetické pole ve středu půlkruhového závitu
Zaměřme se na speciální případ a určeme magnetické pole ve středu půlkruhového závitu s proudem.
Budeme postupovat přímou integrací, připomeňme, vztah pro elementární příspěvek k magnetické indukci
\[\mathrm{d}\vec{B}=\frac{\mu_0}{4\pi}\frac{I\mathrm{d}\vec{l}\times\vec{r}}{r^3}.\]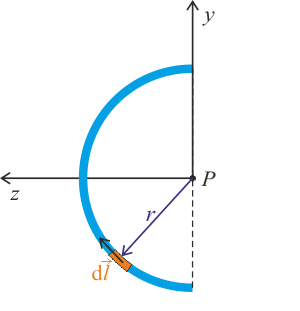
Směr příspěvků od každé infinitezimální části závitu musí být kolmý na \(\vec{r}\) a \(\mathrm{d}\vec{l}.\) Tudíž všechny dílčí příspěvky mají směr osy x, a proto můžeme vztah zjednodušit a omezit se na výpočet velikosti příspěvku
\[\mathrm{d}B=\frac{\mu_0}{4\pi}\frac{I\mathrm{d}{l}{r}\sin\varphi}{r^3},\]kde \(\varphi\) je úhel mezi \(\mathrm{d}\vec{l}\) a \(\vec{r}\). Je zřejmé, že vektory jsou na sebe kolmé, tedy \(\sin\varphi=1\).
\[\mathrm{d}B=\frac{\mu_0}{4\pi}\frac{I\mathrm{d}{l}}{r^2}.\]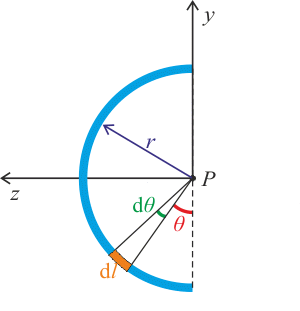
Infinitezimální část půlkruhového vodiče \(\mathrm{d}l\) vyjádříme jako
\[\mathrm{d}l=r\mathrm{d}\theta.\]Potom
\[\mathrm{d}B=\frac{\mu_0}{4\pi}\frac{Ir\mathrm{d}{\theta}}{r^2}=\frac{\mu_0}{4\pi}\frac{I\mathrm{d}{\theta}}{r}.\]Poslední vztah integrujeme podél celého obvodu půlkružnice, tj. budeme integrovat přes úhel \(\theta\),
\[B=\int_0^{\pi}\frac{\mu_0}{4\pi}\frac{I\mathrm{d}{\theta}}{r},\tag{**}\] \[B=\frac{\mu_0}{4\pi}\frac{I}{r}\int_0^{\pi}1\space\mathrm{d}{\theta},\] \[B=\frac{\mu_0}{4}\frac{I}{r}.\]Výsledný směr magnetického pole bude směrem z obrazovky.
Magnetické pole ve středu kružnicového oblouku o velikosti \(\beta\)Jak se změní výpočet, pokud budeme počítat magnetické pole ve středu kružnicového oblouku o velikosti \(\beta\)?
Změní se pouze integrační meze ve výrazu (**) a dostaneme
\[B=\int_0^{\beta}\frac{\mu_0}{4\pi}\frac{I\mathrm{d}{\theta}}{r},\] \[B=\frac{\mu_0}{4\pi}\frac{I}{r}\int_0^{\beta}\mathrm{d}{\theta},\] \[B=\frac{\mu_0 \beta}{4\pi}\frac{I}{r}.\]Pozn.: Pokud vezmeme \(\beta=2\pi\), pak výsledek přesně odpovídá tomu, co nám vyšlo na konci oddílu Řešení.